




Le but de l’analyse de durée de vie (liveness analysis) est de déterminer les information de durée de vie des temporaires. Cette phase est un préalable indispensable à l’allocation de registres par coloriage de graphe qui sera l’objet de la leçon suivante.
Intuitivement, un temporaire est vivant en un point donné du code, si son contenu en ce point peut être lu par la suite. Le mot « vivant » signifie donc surtout utile. Or, si un temporaire est vivant en un point donné du code, son contenu doit se trouver quelque part, idéalement dans un registre machine. Il est clair que si deux temporaires t1 et t2 sont vivants en un même point, alors ces deux temporaires ne peuvent pas représenter le même registre machine. En revanche, si deux temporaires ne sont vivants simultanément en aucun point du code, alors ils peuvent représenter le même registre machine.
Précisons un peu sur un exemple. Soient les deux bout de code suivants, exprimés avec la syntaxe des instructions machine du début chapitre précédent :
|
|
Les « points donnés du code » se situent entre deux instructions, où sont montrés les temporaires vivants. On remarquera, dans le code C2, que t1 n’est pas vivant au deuxième point du programme. Une lecture de t1 suit effectivement (dernière instruction), mais la valeur lue n’est pas celle que t1 contient entre la deuxième et la troisième instruction. On peut donc reformuler la définition des temporaires vivants en disant qu’un temporaire est vivant en un point du programme lorsque, par la suite, il est lu avant d’être écrit. Enfin les points du code sont plutôt repérés par rapport aux instructions, on distingue alors l’entrée d’une instruction et sa sortie.
Pour chaque instruction i, on définit :
Les ensembles Use (i), Def (i) et Succ (i) se définissent instruction par instruction et ce sont justement les informations mises en valeur par le type bizarre Ass.instr de la figure 7.5.
On peut définir Out (i) formellement ainsi :
| Out (i) = | ⎧ ⎨ ⎩ | t | ⎪ ⎪ ⎪ | ∃ i1 ∈ Succ (i), …, in ∈ Succ (in−1), ∧ | ⎧ ⎨ ⎩ |
| ⎫ ⎬ ⎭ |
C’est le pendant exact de la définition des temporaires vivants comme étant ceux qui seront lus avant d’être écrits. De même on définit :
| In (i) = | ⎧ ⎨ ⎩ | t | ⎪ ⎪ ⎪ | ∃ i1=i, i2 ∈ Succ (i1), …, in ∈ Succ (in−1), ∧ | ⎧ ⎨ ⎩ |
| ⎫ ⎬ ⎭ |
En corollaire de ces deux définitions on a les deux égalités :
|
|
Ces deux égalités permettent de calculer Out et In par itération. Avant de le prouver examinons le cas d’une séquence d’instructions. Si les instructions i1 puis i2 se suivent en séquence (ie. on a Succ (i1) = {i2}), alors, les définitions entraînent immédiatement :
| Out (i1) = In (i2) = (Out (i2) ∖ Def (i2)) ⋃ Use (i2) |
Par conséquent, dans le cas d’une séquence d’instructions, les temporaires vivants se calculent facilement en remontant le sens de l’exécution. Dans le cas de nos codes C1 et C2 on a donc en fait :
|
|
Où T est l’ensemble des temporaires vivants en sortie du code. On remarque au passage que les temporaires vivants en entrée de C1 et C2 se déduisent directement de ceux en sortie de ces codes. Ici il suffit d’enlever les temporaires détruits par les codes, qui par ailleurs ne lisent pas les contenus initiaux de t1 et t2.
1 li e, 1 2 ble n, e, L12 3 L13: 4 li r, 1 5 b L16 6 L15: 7 mul r, r, n 8 sub n, n, 1 9 L16: 10 bgt n, $zero, L15 11 L17: 12 move f, r 13 b fact_end 14 L12: 15 li f, 1 16 fact_end: 17 move $v0, f 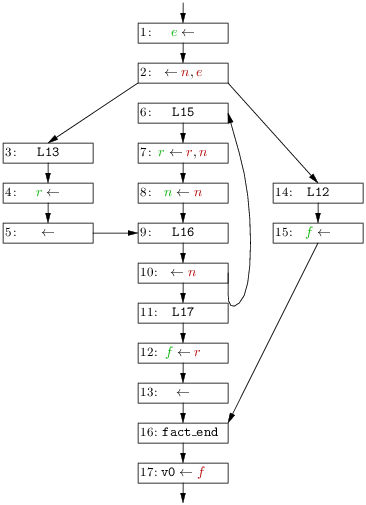
Considérons maintenant l’exemple plus compliqué du code de la figure 8.1. Un graphe de flot met en avant les informations pertinentes pour le calcul des durées de vies, temporaire lus et écrits, contrôle. Sur ce graphe, on constate par exemple que le temporaire e est vivant entre les instructions 1 et 2, tandis que temporaire f est vivant en entrée de l’instruction 17, en raison des séquences 15 (écriture), 16, 17 et 12 (écriture), 13, 16, 17. Le temporaire n est vivant de l’entrée de l’instruction 1 à la sortie de l’instruction 10, mais n’est plus vivant en entrée de l’instruction suivante 11 car aucune instruction ne le lit plus par la suite.
On notera qu’utiliser le graphe de flot revient à approximer les séquences d’instructions réellement exécutées par excès. On suppose que tous les chemins du graphe de flot seront pris lors de l’exécution. Il n’appartient pas à l’analyse de durée de vie de chercher à identifier quels sont les chemins réellement utiles, cette tâche est dévolue à d’autres analyses. Ces autres analyses ne pourront elle-même produire qu’une approximation du contrôle, mais cette approximation sera plus fine que l’approximation grossière qui consiste à considérer que tous les chemins peuvent être pris à l’exécution.
Un code de longueur n cn = [i1 ; … ; in] est une suite de n instructions, qui peuvent s’enchaîner lors d’une exécution du programme. On note [ ] pour la séquence vide. Pour n > 0, on écrit librement cn = [cn−1 ; in] ou cn = [i1 ; cn−1].
Pour une instruction i et un entier naturel k posons :
|
|
Autrement dit, Succk (i) est l’ensemble des codes de longueur k qui peuvent être exécutés après l’instruction i. Outn (i) est défini comme l’ensemble des temporaires vivants en sortie de k en ne considérant que les séquences de code de longueur au plus égale à n.
|
De même on définit Inn (i) en ne retenant que les séquences de longueur limitée par n dans la définition de In (i).
|
Avec deux abus de notation caractérisés, on a aussi défini Out0 (i) = ∅ (Succ0 (i) ne contient pas de séquence de la forme [ck−1 ; ik]) et In0 (i) = ∅ (Succ−1 (i) = ∅). Ces définitions entraînent que les Outn (i) et les Inn (i) sont des suites d’ensembles croissantes au sens large et dont les limites sont Out et In .
|
|
Par ailleurs, on a les deux égalités :
|
|
Montrons par exemple la première égalité. Soit donc t dans Inn+1 (i). En procédant par équivalences et en notant [i ; ck−1] comme [j1 ; j2 ; … ; jk], il vient :
|
|
|
|
|
|
|
Où, dans la dernière proposition, on a effectué un audacieux changement d’indice et noté ck = [i1 ; … ; ik].
Nous pouvons calculer Ink (i) et Outk (i) pour tous les entiers k et toutes les instructions du programme. Il suffit de partir de Out0 (i) = ∅ (La valeur de In0 (i) est indifférente) et d’utiliser constructivement les équations :
|
|
Or, les suites Ink (i) et Outk (i) sont croissantes au sens large, d’après leur définitions, et bornées, puisqu’il y a un nombre fini de temporaires dans un programme donné. Par conséquent ces suites sont stationnaires à partir d’un certain rang où elles valent leurs limites respectives In (i) et Out (i).
Autrement dit, il est temps de remarquer que In (i) est une commodité et que Out (i) est le plus petit point fixe de la fonction :
|
En notant Fi(X) = Use (i) ∪ (X ∖ Def (i)).
Et de fait, nous venons que montrer que Out (i) et In (i) sont la plus petite solution des équations :
|
|
Parfois on se contente donc de définir Out (i) et In (i) comme la plus petite solution de ces équations, vues comme le point fixe d’une fonction. Il faut bien reconnaître que l’intuition est un peu enfouie, en échange d’une définition plus concise. On note aussi qu’il n’est pas immédiatement apparent que la récursion est bien fondée, c’est à dire que la fonction dont on calcule le point fixe est monotone.
Dans cette seconde définition, on aurait tort d’oublier de spécifier plus petit point fixe. En effet, ces équations admettent de nombreuses autres solutions. Soit T(i) des ensemble de temporaires pour le moment arbitraires. On a alors :
|
|
Il suffit alors, pour obtenir une autre solution de trouver des T(i) dont un au moins est non-vide et pour lesquels on a :
|
|
Ce qui est faisable, en posant par exemple, T(i) ≠ ∅ et T(i) ∩ Def (i) = ∅ pour une instruction sans successeur, puis en calculant tous les T(i) par point fixe… On peut aussi donner une solution triviale en posant T(i) = t pour toutes les instructions i, où t est un temporaire qui n’appartient à aucun Def (i).
Nous ne calculons pas les Outk (i) pour eux-mêmes, mais pour leurs limites. Supposons que les instructions i1, i2, … in de notre programme P sont indicées par les entiers d’un intervalle [1,n]. Cela revient à ordonner totalement les instructions et à les désigner par leur rang selon l’ordre choisi. Le calcul de la suite Outk telle que définie demande de maintenir deux tableaux et de procéder selon cet algorithme décrit en Caml de cuisine :
| for i=1 to n do Out (i) <- ∅ done ; do for i=1 to n do Out′ (i) <- Out (i) done ; for i=1 to n do Out (i) <- (∪j ∈ Succ (i) (Out′ (j)∖Def (j)) ∪ Use (j)) done until ∀ i ∈ [1,n], Out (i) = Out ′(i) |
C’est à dire que, à chaque tour de la boucle do…until on calcule les Outk+1 (i) en fonction des Outk (i), conformément à la définition. Mais considérons une nouvelle suite Speedk (i) calculée à l’aide d’un seul tableau :
| for i=1 to n do Speed (n) <- ∅ done ; let encore = ref true in while !encore do encore := false ; for i=1 to n do let prev = Speed (i) in Speed (i) <- (∪j ∈ Succ (i) (Speed (j)∖Def (j))∪ Use (j)) ; encore := !encore || (prev <> Speed (i)) done done |
La définition algorithmique de la suite Speedk (i) est de loin la plus naturelle, mais on peut aussi lui donner la définition plus formelle suivante :
|
|
Avec, rappelons le, Fj(X) = (X ∖ Def (j)) ∪ Use (j). Par monotonie des Fj on a alors :
|
C’est à dire que la suite des Speedk (i) converge également vers Out (i). Par un bon choix de l’ordonnancement des instructions du programme P, on accélère notablement la convergence. Le bon choix est d’ordonner les instructions à l’inverse de l’ordre d’exécution de façon à augmenter la taille de l’ensemble des j ∈ Succ (i), j < i.
Examinons l’effet produit sur l’exemple simple d’un code C exécuté en séquence :
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Avec le choix de Succ (i) = i−1, on voit que, dans le cas d’un code en séquence de n instructions, la stabilisation est atteinte en n+1 étapes pour la suite Outk et 2 étapes pour la suite Speedk .
i Speed0 Speed1 Speed2 In 1 ∅ ∅ ∅ { f } 2 ∅ {f} {f} { f } 3 ∅ {f} {f} ∅ 4 ∅ ∅ ∅ ∅ 5 ∅ {f} {f} {f} 6 ∅ {f} {f} { r } 7 ∅ {r} {r} { r } 8 ∅ { r } { n, r } { n, r } 9 ∅ { n, r } { n, r } { n, r } 10 ∅ { n, r } { n, r } { n, r } 11 ∅ { n, r } { n, r } { n, r } 12 ∅ { n, r } { n, r } { n, r } 13 ∅ { n, r } { n, r } { n, r } 14 ∅ { n, r } { n, r } { n } 15 ∅ { n } { n } { n } 16 ∅ { n } { n } { e, n } 17 ∅ { e, n } { e, n } { n }
Dans le cas d’un contrôle plus complexe, nous avons encore intérêt à ordonner les instructions le plus possible selon l’ordre inverse de leur exécution. Mais satisfaire complètement la contrainte j ∈ Succ (i) entraîne j < i n’est plus possible en raison des boucles. On se contente alors d’un ordre (quasi-)topologique inverse, de sorte que les successeurs sont généralement traités avant leur prédécesseurs. De toute évidence, il convient au moins de traiter les instructions exécutées en séquence dans l’ordre inverse de leur exécution. On peut donc se contenter de l’ordre inverse de la présentation des instructions du programme. Dans le cas de notre compilateur qui ne réordonne pas les traces, cet ordre inverse de la présentation correspond d’ailleurs à ordre (quasi-)topologique inverse.
De fait, une telle numérotation des sommets du graphe de flot de la figure 8.1 permet de calculer les Out (i) en trois itérations, comme le montre la figure 8.2. Ici, on a presque toujours j ∈ Succ (i) entraîne j < i sauf pour Succ (8) = {7, 12}. On a donc, puisque Speed1 (7) = {r} et Speed0 (12) = ∅, Speed1 (8) = (({r} ∖ ) ∪ ∅) ∪ (∅ ∖ ) ∪ ∅) = { r }. À la même itération on a Speed1 (12) = {n, r} puisque le successeur 11 de 12 lit ces deux registres. Dès lors à itération suivante on a, Speed1 (8) = (({r} ∖ ) ∪ ∅) ∪ ({n, r} ∖ ) ∪ ∅) = { n, r }. Le point fixe est atteint comme on s’en rendrait compte en calculant Speed3 (non-montré).
Les In (i) sont montrés pour mémoire.
On notera que le programme présenté est un bout de fonction.
Si on avait analysé le code complet, alors le registre v0 serait
également vivant en sortie de la dernière instruction (numérotée 1),
puisque ce registre est « lu » par l’instruction de retour
j $ra qui vient ensuite.
Le coût du calcul des durées de vie est potentiellement assez élevé. Soit un code de taille n et contenant n temporaires distincts. Que l’on choisisse le calcul des Outk ou des Speedk . Un passage dans la boucle principale se solde par de l’ordre de n opérations ensemblistes, qui chacune coûte disons de l’ordre de n opérations élémentaires. Soit un coût en n2 pour une itération. Dans le pire des cas et à chaque itération un seul des ensembles croît d’un seul élément, et on peut donc itérer au pire n2 fois. Soit un coût en n4 pour l’ensemble du calcul des durées de vie. Heureusement comme nous l’avons vu, ce coût est rarement atteint en pratique. Selon notre mesure rapide et dans le cas du code en séquence, le coût du calcul naïf des Out k est en n3 et celui des Speedk est en n2.
On peut aussi se débrouiller pour diminuer fortement le coût effectif des opérations ensemblistes. Un truc très classique consiste à représenter les ensembles par des vecteurs de bits, les opérations ensemblistes ont alors des pendants directs dans les opérations logiques sur les entiers, (l’union est le ou logique etc.). Dès lors, si le nombre de temporaires distincts est faible (genre inférieur à 32 ou 64) et au prix d’un encodage des temporaires dans les petits entiers, on peut même parler un peu abusivement de coût constant pour les opérations sur les ensembles. En pratique nous n’utiliserons pas cette représentation des ensembles, car elle manque un peu de souplesse.
Un autre gain important en pratique est obtenu en calculant les durées de vie d’abord sur un graphe de flot dont les sommet sont les blocs de base (les blocs de base sont les suites maximales d’instructions nécessairement exécutées en séquence voir section 6.5). En effet, du point de vue des durées de vie les blocs de base se comportent comme de grosses instructions.
Soit donc un bloc b = [i1 ; i2 ; … ; in] avec Succ (ik) = {ik+1} pour k ∈ [1,n−1]. In (b) = In (ii) se calcule alors à partir de Out (b) = Out (in) en constatant Out (ik) = In (ik+1) dans le bloc et en écrivant donc :
|
|
|
Soit plus directement In (b) = (Out (b) ∖ Def (b)) ∪ Use (b), avec :
|
|
L’apparente complexité de la formule des Use ne doit pas troubler, elle se comprend bien si on se rappelle que les temporaires présentés en entrée du bloc ne sont effectivement lus par une instruction ik du bloc, que si leur contenu n’a pas été changé par une instruction précédant ik.
Au prix donc d’un calcul préalable des blocs de base, des Def et des Use de chaque bloc, puis d’une reconstitution des durées de vie instruction par instruction, on diminue notablement le nombre de sommets du graphe sujet à itération. En gros, on divise la nombre de sommets par la taille moyenne des blocs. Le calcul sur le graphe des blocs de base s’impose naturellement dans le cas fréquent d’un compilateur qui maintient la structuration du code selon les blocs de base durant tout le back-end.
Ainsi, dans le cas du code la figure 8.1 on obtient le graphe des blocs de base de la figure 8.3, qui comprend seulement 7 sommets, à comparer aux 17 sommets du graphe de flot des instructions de la figure 8.2.
b Speed0 Speed1 Speed2 In end ∅ ∅ ∅ { f } L12 ∅ { f } { f } ∅ L17 ∅ {f} {f} { r } L16 ∅ { r } { n, r } { n, r } L15 ∅ { n, r } { n, r } { n, r } L13 ∅ { n, r } { n, r } { n } start ∅ { n } { n } {n }
Les informations de durée de vie sont utilisables par plusieurs optimisations du compilateur. Par exemple, si nous avons une instruction t ← …, où … ne fait pas d’effet de bord (typiquement, si nous ignorons les débordements arithmétiques) et que le temporaire t n’est pas vivant en sortie de l’instruction, alors nous pouvons éliminer cette instruction.
Mais, en ce qui nous concerne les durées de vie des temporaires servent à l’allocation de registres. Nous disposons de n registres machines r1, r2, … , rn à répartir entre m temporaires t1, t2, … , tm.
Nous disons que deux temporaires interfèrent si on ne peut pas leur allouer le même registre. La relation d’interférence est certainement non-reflexive, symétrique et non-nécessairement transitive. Il est clair que si deux temporaires ti et tj sont vivants en un même point du programme, on doit leur allouer des registres différents. Notons qu’un temporaire t peut être un registre r (le registre a0 du premier argument exemple). Il n’y a pas lieu, dans ce cas, d’allouer un registre à t=r. Mais on doit évidemment considérer les temporaires qui interfèrent avec t comme ne pouvant pas occuper le registre r.
Le recouvrement des durées de vie est la principale cause
d’interférence entre temporaires. Mais il y en a d’autres.
Considérons d’instruction d’appel de sous-routine
jal f.
Cette instruction écrit dans le registre ra. Pire elle
écrit potentiellement dans tous les registres arguments,
résultat et tous les
caller-saves. Ces conditions interdisent d’allouer un des registres
précités à tout temporaire qui est vivant à travers l’appel de
sous-routine. Et ceci même si nous ne sommes pas stricto-sensu en
présence de durées de vies non-disjointes.
Il peut se trouver des interférence encore plus éloignées des durées
de vie, supposons que la machine ciblée possède
une instruction t ← … dont le résultat ne peut pas être
rangé dans un registre particulier r1, alors le temporaire t
interfère avec le registre r1.
Ce type d’interférence se produit par exemple dans le cas des
processeurs Motorola 680X0, qui possèdent deux classes de registres,
une pour les données et l’autre pour les adresses, toutes les
opérations ne pouvant pas utiliser tous les registres indifféremment.
Mais dans le cas du MIPS, les registres sont réellement d’usage général. Dès lors, et grâce aux « lus » et« écrits » étendus mis en place lors de la sélection d’instructions, on peut calculer les interférences entre temporaires par un simple parcours des instructions i, c’est à dire des sommets du graphe de flot. Ce parcours distingue deux cas :
Ce simple parcours permet de détecter (et d’enregistrer) toutes les interférences d’un programme en assembleur opérant sur les temporaires. En effet, si une instruction produit un résultat dans un temporaire, alors ce temporaire ne peut pas occuper le même registre que tout autre temporaire vivant en sortie de l’instruction (sauf dans le cas du transfert et de sa source, si cette dernière est encore en vie après le transfert). En revanche, une destination de l’instruction peut occuper le même registre que tout temporaire qui n’est pas vivant en sortie de l’instruction.
La relation d’interférence est idéalement représentée par un graphe non-orienté dont les sommets sont les temporaires et dont les arcs expriment l’interférence de deux temporaires. Puisque la relation d’interférence est par définition non-réflexive, il n’y a jamais d’arcs d’un sommet vers lui-même.
On profite du calcul de la relation d’interférence pour calculer une autre relation : deux temporaires sont reliés par un transfert si il existe une instruction move de l’un vers l’autre. On peut représenter cette nouvelle relation sur le graphe d’interférence en ajoutant des arcs distincts des arcs d’interférence.
Reprenons le code en séquence C de la section précédente, ainsi que les informations pertinentes des Def et des Out .
|
On voit alors que les deux temporaires t1 et t2 interfèrent, en raison par exemple de Def (2) = {t2} et Out (2) = {t1, t2}.
Dans le cas de la figure 8.2 et après résumé des informations pertinentes, on obtient le graphe d’interférence suivant.
|
| 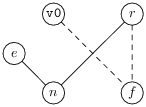 |
Les arcs des « move » sont en pointillés.
On constate d’abord que n et e interfèrent (à cause de e ∈ Def (17) et de n ∈ Out (17)), puis que n et r interfèrent (pour trois raisons, voir les instructions 10, 11 et 14). Au vu du graphe d’interférence, on voit que f, r et e peuvent tous occuper le registre v0. Tandis qu’un autre registre est nécessaire pour n. On notera que les arcs move suggèrent puissamment d’allouer un même registre à v0, f et r, tandis que ce sont bien les arcs d’interférence qui nous disent que c’est possible.
La programmation sur les graphes est notoirement un peu difficile. Cela tient souvent au manque de séparation entre les structures de données qui représentent les graphes et les fonctions qui calculent sur les graphes. En effet il n’est pas évident de définir les graphes par des structures de données abstraites et de garder une bonne efficacité, en raison notamment de la grande variété en pratique des structures de « graphes ». Je m’essaie pourtant ici à un tel exercice dans un souci de clarté.
Nous avons d’abord besoin de manipuler des ensembles de temporaires. Supposons donné un module Smallset qui réalise les opérations courantes sur les ensembles (figure 8.4).
(* Petite réalisation des ensembles. - Les ensembles sont encodés comme des listes ordonnées, selon l'ordre générique de Caml « < » - Toutes les opérations sont en gros linéaires en fonction du cardinal des ensembles passés en argument. *) type 'a set val eqset : 'a set -> 'a set -> bool (* égalité sur les ensembles, ne pas supposer que « = » fonctionne, même si c'est le cas *) val choose : 'a set -> 'a option (* renvoie un élément quelconque *) val singleton : 'a -> 'a set (* créer un singleton *) val of_list : 'a list -> 'a set (* "of_list l" crée l'ensemble dont les éléments sont l, coût en n Log(n) *) val to_list : 'a set -> 'a list (* "to_list s" remvoie la liste des éléments de s *) (* Les fonctions suivantes parlent d'elles-mêmes *) val empty : 'a set val is_empty : 'a set -> bool val mem : 'a -> 'a set -> bool val union : 'a set -> 'a set -> 'a set val union_list : 'a set list -> 'a set (* "union_list l" renvoie la réunion des ensembles de l, coût en n Log(n) *) val diff : 'a set -> 'a set -> 'a set val inter : 'a set -> 'a set -> 'a set val add : 'a -> 'a set -> 'a set val remove : 'a -> 'a set -> 'a set val iter : 'a set -> ('a -> unit) -> unit (* "iter f s" applique f une fois à chaque élément de s, ordre indéfini *)
Les ensembles Smallset sont réalisés par des listes ordonnées, ce qui, par rapport à la réalisation par arbre binaires équilibrés de la bibliothèque standard, pénalise les opérations mem, add etc. au profit des opérations entre ensembles union, diff etc. et surtout de la simplicité et de l’efficacité sur les petits ensembles.
Le gros morceau est la représentation des graphes. Soit donc le module Graph dont l’interface est donnée à la figure 8.5.
(********************) (* Graphes orientés *) (********************) (* en cas de malheur *) exception Error of string (* Types de sommets et des graphes *) type 'a node and 'a t val create : 'a -> 'a t (* Créer un nouveau graphe, initialement vide, les sommets contiendront l'information 'a *) val new_node : 'a t -> 'a -> 'a node (* « new_node g i » ajoute un noeud d'information i au graphe g par effet de bord *) val new_edge : 'a t -> 'a node -> 'a node -> unit (* « new_edge g n1 n2 » ajoute un arc de n1 vers n2, si il n'existe pas déjà *) val nodes : 'a t -> 'a node list (* Tous les noeuds, dans l'ordre de leur création *) val info : 'a t -> 'a node -> 'a (* Le contenu d'un noeud *) val succ : 'a t -> 'a node -> 'a node list (* Les successeurs d'un noeud *) val iter : 'a t -> ('a node -> unit) -> unit (* « iter g f » itère la fonction f sur les noeuds (ordre de création) *) val debug : out_channel -> (out_channel -> 'a node -> unit) -> 'a t -> unit (* Affichage pour le debug *)
L’interface est suffisament commentée. On remarquera que le module
Graph se charge de garantir l’existence d’au plus
un arc entre deux sommets.
Le type des sommets (ou nœuds) 'a node est abstrait et
paramétré par le type 'a des informations associées aux sommets.
On passe donc logiquement en argument une valeur de type 'a à
la fonction new_node de création des sommets.
Le typage de Caml impose de passer une information bidon lors de la
création du graphe (fonction create).
Dans le cas du graphe de flot, les informations à associer aux sommets sont, une instruction, et ses ensembles Use , Def , In et Out . On définit donc le type suivant :
| type flowinfo = { instr : Ass.instr ; (* instruction *) def : temp set; use : temp set; (* détruits et lus *) mutable live_in : temp set; (* sans commentaire *) mutable live_out : temp set; } type flowgraph = flowinfo Graph.t (* Type des graphes de flots décorés des live-in/live-out *) val flow : Ass.instr list -> flowgraph (* Fabrication du graphe de flot, décoré par les durées de vie *) |
Les champs live_in et live_out sont mutables, car ils ne
sont pas connus à la création du graphe, mais calculés par la suite.
De fait, la fonction flow
est très simple : création du graphe, puis calcul des durées de vie.
| let flow code = let g = mk_graph code in fixpoint g ; g |
Pour fixer un peu les idées voici une fonction mk_graph
possible.
On crée le graphe en deux temps, d’abord les sommets :
| open Smallset let mk_info i = match i with | Oper (_, src, dest, _) -> {instr=i ; def = of_list dest ; use = of_list src ; live_in = empty ; live_out = empty} | Move (_,src, dest, _) -> {instr = i ; def = singleton dest ; use = of_list src ; live_in = empty, live_out = empty} | Label (_,_) -> {instr = i ; def = empty ; use = empty ; live_in = empty, live_out = empty} let lab2node = Hashtbl.create 17 let rec mk_nodes g = function | [] -> () | i::rem -> let n = Graph.mk_node g (mk_info i) in begin match i with | Label (_,lab) -> Hashtbl.add lab2node lab n | _ -> () end ; mk_nodes g rem |
C’est la fonction mk_nodes ci-dessus qui ajoute les sommets au
graphe g passé en argument. Elle procède par un simple parcours
de la liste d’instructions (assembleur) passée en second argument. À
chaque somment correspond des informations, regroupant l’instruction
elle même (champ instr) les temporaires lus et écrits
(champs use et def). Les informations de liveness
(champs live_in et live_out) sont initialisées à
l’ensemble vide.
Au passage, on remplit une table de hachage lab2node qui
réalise une association des étiquettes aux
nœuds, utile pour créer les arcs résultant des sauts dans une
seconde étape.
Les arcs sont créés par un parcours de la liste des sommets du
graphe (Obtenue à partir du graphe g, par
Graph.nodes g) qui, rappelons le, portent une instruction dans leur
champ instr de leur information La création des arcs diffère
selon que cette instruction est un saut (et alors il faut aller
chercher les sommets cibles à partir de leurs étiquettes et à l’aide
de la table de hachage de l’étape précédente) ou une instruction
qui transfère le contrôle en séquence (et alors la cible de l’arc est
l’instruction suivante, qui doit exister). Il est donc critique que
la liste des sommetes du graphe reflète l’ordre de création des
sommets, qui est ici l’ordre des instructions dans la liste initiale.
| let rec mk_edges g nodes = match nodes with | [] -> () | n::rem -> begin match (Graph.info g n).instr with | Oper (_,_,_,Some labs) -> (* Saut *) List.iter (fun lab -> let jump_to = try Hashtbl.find lab2node lab with Not_found -> assert false in Graph.new_edge g n jump_to) labs | _ -> (* Contrôle en séquence *) match rem with | next::_ -> Graph.new_edge g n next | _ -> assert false end ; mk_edges g rem |
On posera ensuite tout simplement :
| let mk_graph code = let g = Graph.create (mk_info (Oper ("", [], [] ,None))) in mk_nodes g code ; mk_edges g (Graph.nodes g) ; g |
En ce qui concerne la fonction fixpoint, le plus simple est
sans doute de partir des « définitions » par point fixe des
ensembles In et Out .
|
|
Le calcul accéléré (section 8.1.3) vient naturellement
en transformant les équations en affectations des champs mutables
live_in et live_out. Il est laissé en exercice.
Le graphe d’interférence est non-orienté, il possède deux sortes d’arcs (pour les interférence et les move) et il n’y pas d’arcs d’un sommet vers lui-même. Ces différences justifient un nouveau module des graphes Sgraph (figure 8.6).
(****************************************) (* Graphes non-orientés *) (* - Les sommets contiennent des 'a *) (* - Les arcs sont étiquetés par des 'b *) (****************************************) type ('a, 'b) t type 'a node exception Error of string (* Erreur, avec un message *) (* Créer un nouveau graphe *) val create : 'a -> ('a, 'b) t val new_node : ('a, 'b) t -> 'a -> 'a node (* créer un nouveau sommet ajouté graphe par effet de bord *) val new_edge : ('a, 'b) t -> 'a node -> 'a node -> 'b -> unit (* « new_edge g n1 n2 l » , ajoute un arc étiqueté par l entre n1 et n2. L'arc n'est pas crée lorsque : - Il existe déjà, - ou n1=n2 *) val exists_edge : ('a, 'b) t -> 'a node -> 'a node -> 'b -> bool (* exists_edge g n1 n2 l, teste l'existence d'un arc entre n1 et n2 et étiquetté par l *) val iter : ('a, 'b) t -> ('a node -> unit) -> unit (* itérer une fonctions sur tous les sommets du graphe (ordre de création) *) (******************) (* Lire le graphe *) (******************) val nodes : ('a, 'b) t -> 'a node list (* liste de tous les noeuds, (ordre de creation) *) val info : ('a, 'b) t -> 'a node -> 'a (* contenu d'un sommet *) val adj : ('a, 'b) t -> 'a node -> 'b -> 'a node list (* voisins d'un sommet *)
On remarquera surtout que le type des graphes ('a, 'b) Sgraph.t est
maintenant paramétré à la fois par le type du contenu des sommets
et celui des arcs.
Fort logiquement les fonctions new_edge (création des arcs) et
adj (retrouver les voisins d’un sommet) prennent un argument
de type 'b qui identifie la sorte d’arcs concernée.
Ainsi le type des graphes d’interférence est le suivant :
| (* Sortes d'arcs du graphe d'interférence *) type ilab = Inter | Move_related (* Contenu des noeud du graphe d'interférence *) type interference = { temp : temp; (* un temporaire *) (* Les champs suivants sont utiles pour l'allocation de registres *) mutable color : temp option ; mutable occurs : int ; mutable degree : int ; mutable elem : ((interference Sgraph.node) Partition.elem) option ; } type igraph = (interference, ilab) Sgraph.t val interference : flowgraph -> igraph |
La fonction interference prend en argument le graphe de flot décoré par les durées de vie et renvoie le graphe d’interférence. Elle procède par un simple parcours des sommets du graphe de flot. Pour chaque instruction i du programme (ie. chaque sommet du graphe de flot), on a deux cas.
Le code assembleur contient en plus des temporaires et des registres d’usage général, des références aux registres spéciaux (genre gp, zero, …). Ces registres dits speciaux sont exclus du mécanisme général d’allocation des registres par nécessité (zero, …) ou par choix (sp, fp, …). Il sont définis dans le module Spim.
Il y a au moins deux façons de traiter proprement les registres spéciaux. Je choisis de les exclure complètement, c’est à dire de ne calculer ni leurs durées de vie, ni leur interférences. Il convient alors de ne pas inclure de registres spéciaux dans les ensembles Def et Use du graphe de flot et de ne pas les introduire dans le graphe d’interférence. Cette solution a l’avantage de produire des graphes plus lisibles.
L’autre solution est de ne pas distinguer registres spéciaux et d’usage général, jusqu’à l’allocation de registres qui doit dans ce cas traiter différemment les deux classes de registres.
Considérons un petit programme Pseudo-Pascal.
| function fact (n : integer) : integer; var r : integer ; begin if n <= 1 then fact := 1 else begin r := 1 ; while n > 0 do begin r := r * n; n := n-1 end ; fact := r end end; |
Il s’agit de la fonction fact qui nous a déjà servi d’exemple (cf. la figure 8.1).
Voici le graphe de flot complet de la fonction fact. On se limite à quatre registres, v0, ra, a0 (argument), et s0 (callee-save).
| fact: # <= # $a0 $s0 $ra subu $sp, $sp, fact_f # <= # $a0 $s0 $ra move $112, $ra # $112 <= $ra # $a0 $s0 $112 move $113, $s0 # $113 <= $s0 # $a0 $112 $113 move $108, $a0 # $108 <= $a0 # $108 $112 $113 li $114, 1 # $114 <= # $108 $112 $113 $114 ble $108, $114, L12 # <= $108 $114 # $108 $112 $113 L13: # <= # $108 $112 $113 li $109, 1 # $109 <= # $108 $109 $112 $113 b L16 # <= # $108 $109 $112 $113 L15: # <= # $108 $109 $112 $113 mul $109, $109, $108 # $109 <= $108 $109 # $108 $109 $112 $113 sub $108, $108, 1 # $108 <= $108 # $108 $109 $112 $113 L16: # <= # $108 $109 $112 $113 bgt $108, $zero, L15 # <= $108 # $108 $109 $112 $113 L17: # <= # $109 $112 $113 move $107, $109 # $107 <= $109 # $107 $112 $113 b fact_end # <= # $107 $112 $113 L12: # <= # $112 $113 li $107, 1 # $107 <= # $107 $112 $113 fact_end: # <= # $107 $112 $113 move $v0, $107 # $v0 <= $107 # $v0 $112 $113 move $115, $112 # $115 <= $112 # $v0 $113 $115 move $s0, $113 # $s0 <= $113 # $v0 $s0 $115 addu $sp, $sp, fact_f # <= # $v0 $s0 $115 j $115 # <= $v0 $s0 $115 # |
Pour chaque instruction sont montrés les Def , les Use et les temporaires vivants en sortie. Les points notables sont :
Voici ensuite graphe d’interférence :
$112 <=> $v0 $107 $109 $114 $108 $113 $s0 $a0 $ra <=> $a0 <=> $113 $112 $s0 <=> $115 $v0 $112 $113 <=> $115 $v0 $107 $109 $114 $108 $112 $a0 $108 <=> $109 $114 $113 $112 $114 <=> $113 $112 $108 $109 <=> $113 $112 $108 $107 <=> $113 $112 $v0 <=> $s0 $115 $113 $112 $115 <=> $s0 $113 $v0
On remarque :
Enfin voici le graphe des moves :
$112 <=> $115 $ra $ra <=> $115 $112 $a0 <=> $108 $s0 <=> $113 $113 <=> $s0 $108 <=> $a0 $114 <=> $109 <=> $v0 $107 $107 <=> $v0 $109 $v0 <=> $109 $107 $115 <=> $ra $112
Ce graphe suggère nettement comment répartir les registres entre les temporaires. Par exemple, on aura, dans le code final, intérêt à remplacer les temporaires 109 (variable r) et 107 (variable fact) par v0. Le graphe d’interférence indique que c’est possible car ces temporaires n’interfèrent pas avec v0.
Par rapport à la définition directe « il y a un arc move entre t et t′ quand il y a un transfert entre t et t′ » le graphe présenté représente en fait une fermeture de la relation de transfert simple. Deux temporaires sont en relation quand il y a une chaîne de transfert entre eux, dont aucun temporaire intermédiaire n’est un registre machine. On le voit par exemple dans le cas du temporaire 109 qui est en relation avec v0 par l’intermédiaire du temporaire 107.


