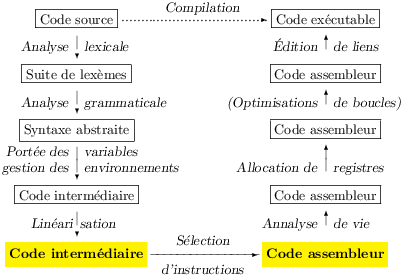




Le source de la passe de sélection des instructions est donc le code intermédiaire canonisé et linéarisé (voir le chapire précédent), sa cible est le langage assembleur de la machine ciblée, c’est à dire dans notre cas celui du MIPS (voir la section 2.2).
Les instructions du MIPS opèrent principalement sur le schéma « trois-adresses », c’est à dire que la plupart des instructions effectuent une opération sur deux registres machines et rangent le résulat dans un troisième. Par exemple l’addition :
| add r1, r2, r3 |
Nous noterons ce style d’instruction r1 ← r2+r3. En fait la deuxième source r3 peut aussi être un petit entier sur 16 bits. Il d’agit d’une instruction machine différente, même si elle a le même mnémonique add, on la note r1 ← r2+i16. Deux autres instructions importantes du MIPS sont l’écriture et la lecture de la mémoire (store et load).
| sw r1, i16(r2) # charge le contenu de r1 dans la case mémoire d'adresse i16+r2 lw r1, i16(r2) # idem pour lire la mémoie |
Nous les noterons [i16+r2] ← r1 et r1 ← [i16+r2] (rappelons que l’adresse mémoire écrite ou lue est la somme du petit entier i (seize bits) et du contenu du registre r2 (trente-deux bits). Le chargement en registre d’une constante ou d’une adresse (une étiquette) s’effectue par les instructions :
| li r1, i la r1, l |
Notées r1 ← i et r1 ← l. Du point de vue strictement machine, ces instructions sont en fait identiques : charger un entier en registre. Le mnémonique la indique simplement à l’assembleur de la présence d’une étiquette à resoudre. Toutefois, si l’entier tient sur 16 bits, il s’agit d’une unique instruction machine et de deux sinon. Pour distinguer ces deux cas, donnons nous deux instructions r1 ← i16 et r1 ← i32 (pour l’instruction la nous ne pouvons rien faire). Enfin, il reste une dernière instruction importante, celle qui transfère le contenu d’un registre r2 dans un autre r1
| move r1, r2 |
La sélection opérée sur une instruction du code intermédiaire consiste à parcourir l’arbre de cette instruction en émettant la ou les instructions machines qui la réalisent. Il s’agit essentiellement d’un parcours postfixe, on compile les arguments avant d’emettre l’instruction machine qui realise de calcul demandé par un nœud. Chaque bout de code rend son résultat dans un temporaire frais alloué pour l’occasion.
Soit par exemple l’instruction Move (t0, Mem (Bin (Plus , Temp t1, Const i16))), présentée sous forme d’arbre avec la simplification de montrer l’addition comme un arbre binaire :
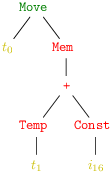
On obtient alors ces trois codes possibles, qui tous sont corrects.
|
|
|
Le premier code prend au pied de la lettre la notion de sélection comme parcours postfixe, le second remarque l’existence d’une instruction d’addition dont la seconde source est un entier et que l’on peut éviter un transfert de registre, le dernier code se rend compte d’entrée de jeu de tout le pouvoir de l’instruction de chargement en mémoire du MIPS.
Une bonne façon de voir est de regrouper les nœuds de l’arbre qui se retrouvent réalisés par une même instruction machine. On appelle traditionellement ces regroupement des tuiles (tiles). On obtient alors logiquement les recouvrements de l’arbre en quatre, deux ou une tuiles de la figure 7.1.
On notera que les temporaires (et l’entier i16) sont laissés en dehors des tuiles. En effet, ils n’ont pas d’intérêt, seule compte l’instruction sélectionnée. Les malins remarqueront que, pour bien recouvrir tout les nœuds de l’arbre, il nous faudrait une tuile supplémentaire recouvrant le nœud Temp et correspondant à aucune instruction. Sur notre exemple nous pouvons dresser deux tableaux des tuiles correspondant à chaque instruction machine (voir figure 7.2). Il y a un tableau pour les expressions du code intermédiaire, et un autre pour ses instructions.
Tuiles à recouvrir les expressions r1 ← i16 : 
r1 ← r2 + r3 : 
r1 ← r2 + i16 : 
r1 ← [i16 + r2] : 
Tuiles à recouvrir les instructions r1 ← r2 : 
r1 ← [i16 + r2] : 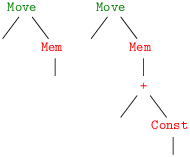
La sélection revient à couvrir les constructions du code intermédiaire à l’aide de tuiles définies à partir du jeu d’instruction de la machine. Pour une instruction donnée, le jeu de tuile associé exprime son « pouvoir couvrant ». Ainsi, en tenant compte de la commutativité de l’addition, le jeu de tuiles « à couvrir les expressions du code intermédiaire » de l’instruction machine r1 ← r2 + i16 est constitué de deux tuiles.

Tandis que l’instruction machine r1 ← [i16 + r2] possède quatre tuiles à couvrir les instructions du code intermédiaire.
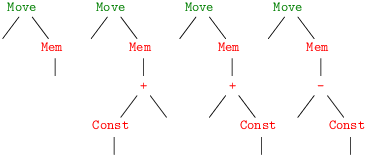
La dernière tuile provient de l’identité x − i = x + (−i). Une tuile du même genre ne semble pas utile dans le cas de l’instruction r1 ← r2 + i16 car la tuile de l’instruction de soustraction immédiate r1 ← r2 − i16, couvre ce cas. Si les coûts de l’addition et de la soustractions étaient différents, nous pourrions adopter l’une ou l’autre tuile1.
Une fois les tuiles définies, le jeu consiste donc à en recouvrir les arbres du code intermédiaire. Si on associe à chaque instruction machine (et donc aux tuiles) un coût, on peut distinguer deux classes de recouvrement d’intérêt particulier.
Le coût des instructions machine peut par exemple s’estimer en considérant le nombre de cycles du processeur nécessaires pour les exécuter. Dans le cas du MIPS il suffit alors de compter le nombre d’instructions machines des expansions des instructions de l’assembleur (celles que nous sélectionnons en fait). Cette estimation ne rend bien entendu pas compte exactement du temps d’exécution d’une instruction, qui dépend de nombreux autres facteurs (état des caches, du pipeline, …). Une estimation encore plus simple est d’associer un coût unité à chaque instruction de l’assembleur, il y a alors confusion entre coût, nombre de tuiles et longueur de la séquence d’instructions assembleur générée. Toutes ces estimations sont grossièrement fausses dans le cas de la multiplication et de la division qui coûtent toujours plus qu’une instruction ordinaire. Pour le moment gardons juste ce point en mémoire.
Selon les définitions, un optimum est forcément optimal mais pas le contraire. De fait, l’optimal est un optimun local. La différence de coût entre optimal et optimum n’apparaît que sur des recouvrement plus compliqués que le nôtre et surtout pour un jeu d’instructions plus étendu. Cette différence est de toute façon rarement significative en pratique. Or, il existe un algorithme simple et efficace pour atteindre un optimal, tandis que trouver un optimum demande un algorithme de programmation dynamique plus compliqué et coûteux. Nous nous cantonerons donc à l’optimal, ce qui n’est pas le cas des concepteurs de générateurs de sélecteurs d’instructions. Ces générateurs sont de véritables compilateurs qui transforment des jeux de tuiles (et de coûts) en des programmes réalisant la sélection d’instructions.
L’intérêt de ces outils n’est pas évident dans le cas des processeurs RISC.
Ainsi, quand le jeu d’instruction est simple, on rechigne à se donner la peine d’apprendre le fonctionnement d’un outil qui réalise un travail que l’on peut faire soi-même assez facilement. On comparera par exemple avec l’analyse grammaticale : la complexité de l’analyse des grammaires LALR(1) et leur expressivité justifient l’emploi d’un outil genre yacc.
En effet, la recherche d’un recouvrement optimal se fait à partir de la racine de l’arbre, on essaie d’abord toutes les tuiles possibles en retenant celle de moindre coût parmi les tuiles qui convienent ; dans le modèle simple de coût, la tuile à choisir est celle qui a le plus nœuds. Ensuite, on opère récursivement sur les sous-arbres qui dépassent de la tuile. Cela semble peut être un peu compliqué, mais l’idée des tuiles précède la venue des langages genre ML, qui possèdent la construction du filtrage (pattern matching). Une tuile est réellement une description des nœuds du sommet d’un arbre avec des trous, c’est à dire exactement un motif (pattern) au sens de ML, et la recherche de l’optimal se fait donc par une bête fonction récursive qui filtre son argument selon les tuiles.
Par exemple, le programme Caml de la figure 7.3 génère du bon code et n’est guère moins concis qu’une spécification équivalente pour un générateur de sélecteurs.
(* Les entiers relatifs de l'intervalle [−2b−1… 2b−1[ sont représentables sur b bits *) let seize_bits i = -(1 lsl 15) <= i && i < (1 lsl 15) let emit s = Printf.printf "%s\n" let rec emit_exp e = match e with | Temp _ -> () (* cas de base, pas d'instruction *) (* Constante entière *) | Const i -> emit "r1 ← i" (* l'assembleur distingue r1 ← i16 et r1 ← i32 *) (* Addition *) | Bin (Plus, Const i, e2) when seize_bits i -> emit_exp e2 ; emit "r1 ← r2 + i16" | Bin (Plus, e1, Const i) when seize_bits i -> emit_exp e1 ; emit "r1 ← r2 + i16" | Bin (Plus, e1, e2) -> emit_exp e1 ; emit_exp e2 ; emit "r1 ← r2 + r3" (* Accès mémoire *) | Mem (Bin (Plus, Const i, e2)) when seize_bits i -> emit_exp e2 ; emit "r1 ← [i16 + r2]" | Mem (Bin (Plus, e1, Const i)) when seize_bits i -> emit_exp e1 ; emit "r1 ← [i16 + r2]" | Mem (Bin (Sub , e1, Const i)) when seize_bits (-i) -> emit_exp e1 ; emit "r1 ← [i16 + r2]" (* i16 est -i *) | Mem e -> emit_exp e ; emit "r1 ← [0 + r2]" | ... and emit_stm stm = match stm with ...
En fait, à condition de présenter les motifs les plus spécifiques en premier, c’est le compilateur Caml qui fait le plus gros travail : la compilation du filtrage On notera aussi que l’emploi de la clause when qui résout oportunément le problème des entiers sur 16 bits.
Les registres réels du processeurs sont connus de la sélection, pour émettre certaines instructions qui opèrent sur des registres fixés, mais aussi pour réaliser les conventions d’appel. Ces registres sont représentés par des temporaires, le module Gen définissant un tableau de temporaires registers à cet effet. Le sélecteur assigne un usage à ces temporaires pré-alloués. Le plus pratique est de ranger chaque temporaire de registre machine dans une variable qui porte son nom conventionel. À l’intention de l’assembleur on se donne aussi un tableau de chaînes des noms conventionnels. (figure 7.4).
let r = Array.sub registers 0 32 (* Le MIPS a 32 registres *) let zero = r.(0) and at = r.(1) and v0 = r.(2) ... and fp = r.(30) and ra = r.(31) let name_of_register = [| "zero"; "at"; "v0"; "v1"; "a0"; "a1"; "a2"; "a3"; "t0"; "t1"; "t2"; "t3"; "t4"; "t5"; "t6"; "t7"; "s0"; "s1"; "s2"; "s3"; "s4"; "s5"; "s6"; "s7"; "t8"; "t9"; "k0"; "k1"; "gp"; "sp"; "fp"; "ra"; |] (* Usage standard des registres MIPS *) let arg_registers = [a0; a1; a2; a3] and res_registers = [v0] and caller_save_registers = [t0; t1; t2; t3; t4; t5; t6; t7; t8; t9] and callee_save_registers = [ra ; s0; s1; s2; s3; s4; s5; s6; s7] (* Une autre convention, 3 registres disponibles let arg_registers = [a0] and res_registers = [v0] and caller_save_registers = [] and callee_save_registers = [ra] *)
On regroupe ensuite facilement les registres par catégories. Un fois encore, il s’agit de conventions que nous pouvons changer, afin par exemple de tester l’allocateur de registres sous pression. Toutefois, le registre ra doit impérativement être inclus dans la liste des callee-saves, nous verrons pourquoi dans la section sur les fonctions.
Nous devons sélectionner les instructions mais pas encore choisir les registres. Un type Ass.instr explicitant les temporaires et leur usage mais paramétré par les mnémoniques permet cette opération étrange à première vue (figure 7.5).
type temp = Gen.temp type label = Gen.label type instr = | Oper of string * temp list * temp list * label list option (* Oper (mnémonique, sources, destinations, sauts) *) | Move of string * temp * temp | Label of string * label
Examinons un peu le principe de l’instruction la plus générale Oper. Soit donc la presqu’instruction MIPS add t1, t2, t3. Ce n’est pas tout à fait une instruction de l’assembleur en raison des temporaires qui prennent la place des registres. On la représente par :
| Oper ("add ^d0, ^s0, ^s1", [t2 ; t3], [t1], None) |
La chaîne est l’instruction de l’assembleur, avec les registres arguments de
remplacés par ^di ou ^si.
Ces chapeaux étranges désignent l’emplacement dans l’instruction des
registres lus et écrits par elle.
L’entier i désigne le i plus unième registre de chaque catégorie.
La numérotation s’entend par rapport aux listes de temporaires qui
suivent, la première liste contient les registres lus (ou sources, d’où
le « s ») la seconde les registres écrits (ou destinations, d’où le « d »).
Enfin le dernier argument indique les sauts effectués par
l’instruction, ici il n’y en pas, donc c’est None.
Plus précisément, None signifie que le contrôle passe
nécessairement à l’instruction suivante.
Selon cette représentation l’instruction d’addition « immédiate » add t1, t2, 20 sera donc :
| Oper ("add ^d0, ^s0, 20", [t2], [t1], None) |
Les sauts s’expriment aussi avec Oper. Il faut d’abord bien voir que les étiquettes ont une représentation conforme à nos besoins (type Gen.label) et une représentation externe conforme aux exigences lexicales de l’assembleur (genre que des caractères alphanumériques). On passe de la repésentation interne à la représentation externe par la fonction Frame.string_label. Soit donc une étiquette l de représentation externe L123. Alors, un saut vers cette étiquette s’exprime comme :
| Oper ("b L123", [], [], Some [l]) |
Pour l’instruction de saut conditionnel beq t1, t2, L123 on aura donc :
| Oper ("beq ^s0, ^s1 L123", [t1 ; t2], [], Some [l ; l′]) |
Surprise ! Une deuxième étiquette apparaît dans les branchements, c’est celle de la condition invalidée, qui est le dernier argument de l’instruction Cjump du code intermédiaire.
Après canonisation, la définition de cette seconde étiquette suit nécessairement en séquence. Voilà une occasion de découvrir l’encodage de la pose des étiquettes dans le code assembleur. Soit donc L321 la représentation externe de l’étiquette l′, on aura :
| Label ("L321:", l′) |
On note le « : » suffixant l’étiquette.
Enfin l’insruction move t1, t2 de transfert de registre à registre est particularisée, en raison de son importance lors de l’allocation de registres, dont une des missions est justement de supprimer les moves si il est arrivé à assigner le même registre machine à t1 et t2.
| Move ("move ^d0, ^s0", t2, t1) |
Ne vous laissez pas surprendre par l’échange des arguments, toutes les conventions ont leurs défauts.
Les instructions assembleur seront au final donées en argument à une fonction emit comme dans le code de la figure 7.3. Mais là où le selecteur théorique affichait l’instruction selectionnée, le selecteur réel doit renvoyer une liste d’instructions machine. Plutôt que de faire renvoyer la liste d’instruction par le selecteur, je préfère conserver une programmation impérative (et oui ça m’arrive) et donc continuer d’appeler la « fonction » emit pour son effet de bord. La fonction emit doit donc maintenant accumuler les instructions dans une structure de donnée quelconque, que j’appelle une table (figure 7.6).
type 'a t val create : 'a -> 'a t (* Créer une table *) val emit : 'a t -> 'a -> unit (* Ajouter un element à la fin de la table *) val trim_to_list : 'a t -> 'a list (* Vider la table dans une liste *)
La table est une structure impérative, on définira emit ainsi :
| let nop = Oper ("nop", [], [], None) (* instruction qui ne fait rien *) let my_table = Table.create nop (* le typage de Caml exige cet argument *) let emit ins = Table.emit my_table ins |
Il se révèle pratique de regrouper les cas semblables à l’aide de fonctions d’émission spécifiques. Par exemple, pour les opérations arithmétiques on peut écrire :
| let memo_of_op = function | Uplus -> "addu" (* addition non signée, pour les calculs d'adresse *) | Plus -> "add " | Minus -> "sub " ... | Eq -> "seq " | Ne -> "sne " (* opérations booléennes *) let emit_op3 op d s0 s1 = emit (Oper (memo_of_op op^" ^d0, ^s0, ^s1"),[s0 ; s1], [d], None) let emit_op2 op d s i = emit (Oper (memo_of_op op^" ^d0, ^s0, "^string_of_int i),[s], [d], None) let emit_move d s = emit (Move ("move ^d0, ^s0", s, d)) |
Enfin, la fonction de sélection emit_exp doit maintenant rendre le temporaire destination de l’instruction émise. La figure 7.7 décrit un selecteur complet pour les expressions. On peut comparer avec la figure 7.3 qui décrit l’algorithme employé, donc un sélecteur « théorique ».
let rec emit_exp e = match e with (* Temporaire *) | Temp t -> t (* Constantes *) | Const 0 -> zero (* c'est un registre *) | Const i -> let d = new_temp () in emit (Oper ("li ^d0, "^string_of_int i, [], [d], None)) ; d | Name l -> let d = new_temp () in emit (Oper ("la ^d0, " ^label_string l, [], [d], None)) ; d (* Opérations *) | Bin ((Plus|Times|Uplus) as op, Const i, e2) -> emit_binop op e2 (Const i) | Bin (op, e1, e2) -> emit_binop op e1 e2 (* Accès mémoire *) | Mem e -> let d = new_temp () and s,i = emit_addr e in emit (Oper ("lw ^d0, "^string_of_int i^"(^s0)", [s], [d], None)) ; d (* Les expressions sont canoniques *) | Call (_,_) -> assert false and emit_binop op e1 e2 = match e2 with | Const i when seize_bits i -> let s = emit_exp e1 and d = new_temp () in emit_op2 op d s i ; d | _ -> let s0 = emit_exp e1 and s1 = emit_exp e2 and d = new_temp () in emit_op3 op d s0 s1 ; d and emit_addr e = match e with (* seuls cas intéressants à repérer *) | Bin (Uplus, Temp r, Const i) when seize_bits i -> r,i | Bin (Uplus, Const i, Temp r) when seize_bits i -> r,i (* cas général *) | _ -> emit_exp e, 0
Les temporaires renvoyés sont pour la plupart des temporaires frais,
sauf pour les cas particuliers d’un temporaire Temp t
(t est renvoyé)
et de la constante entière 0 (le registre zero est renvoyé).
On notera l’astuce employée pour exploiter l’éventuel seconde source
entière et l’usage de fonctions appelées quand le sommet de la tuile
identifie l’instruction lw ou
le groupe des instructions arithmétiques.
On remarquera aussi que le selecteur n’essaie pas d’effectuer les
opérations dont les deux arguments sont connus. Cette mission est
dévolue à des phases d’optimisation
(avec notre représentation des instructions machines ce type
d’optimisation n’est possible qu’en amont).
Enfin, j’ai un peu triché avec les additions signées et non-signées pour
avoir plus de tuiles dans le sélecteur théorique.
La selection sur les instructions du code intermédiaire ne sera pas décrite en détail : c’est exactement la même chose que pour les expressions. La seule différence notable est que les instructions du code intermédiaire n’ont pas de valeur. La fonction emit_stm se contentera donc d’émettre le code machine qui exécute son argument et renverra void (() de type unit).
| val emit_stm : Code.stm -> unit |
Le sélecteur est chargé de réaliser les conventions d’appel de la machine ciblée. Les conventions qui nous intéressent ici sont surtout celles qui déterminent les rapports entre l’usage des registres et les fonctions. Ces conventions pour le MIPS sont décrites à la section 2.4.6. On a principalement.
Après canonisation, l’appel de fonction n’apparaît plus que dans les instructions du code intermédiaire. Suposons donc un appel de procédure (de fonction) à deux arguments.
|
|
(En fait l’argument de Call est une liste d’expressions.)
Nous devons d’abord émettre les instructions qui calculent la valeur
de e1 et la rangent dans a0, puis celles qui calculent la valeur
de e2 dans a1.
Ensuite nous pouvons émettre l’instruction d’appel de sous-routine
jal (figure 7.8).
let emit_jal lab sources dests = emit (Oper ("jal "^lab, sources, dest, None)) let emit_call2 f e1 e2 = emit_move a0 (emit_exp e1) ; emit_move a1 (emit_exp e2) ; let lab = Gen.label_string (Frame.frame_name f) in emit_jal lab [a0; a1] (ra::v0::args_registers@caller_save_registers) let is_fun = match Frame.frame_result f with Some _ -> true | None -> false in if is_fun then Some v0 else None
Examinons d’un peu plus près l’instruction
jal. L’adresse de la sous-routine
est extraite du frame de la fonction, à l’aide de la fonction idoine
du module Frame.
On constate ensuite que, du point de vue de son dernier argument,
l’instruction ne branche pas : elle s’exécute en séquence.
Le point de vue est donc de voir l’appel de sous-routine comme une
instruction ordinaire.
En fait, cette instruction ordinaire remplace les instructions
du corps de la fonction f, que nous ne pouvons pas connaître en général
puisqu’elles peuvent être émises après l’émission de
l’appel.
Les sources de cette instruction sont les deux registres arguments
a0 et a1, même si ces registres n’apparaissent pas
explicitement dans le mnémonique (pas de ^s0, ni de
^s1).
On découvre ensuite une liste impressionante de destinations.
La présence de ra ne surprend pas car l’instruction
jal écrit dedans,
la présence de v0 non plus car si f est une fonction, elle y
rangera son résultat, comme le dit emit_call2 elle même.
Mais si f est une procédure ? Et bien f peut aussi écrire
dans v0, si par exemple f appelle une autre fonction.
Il en va de même pour tous les registres arguments et tous les
registres caller-save2.
Les callee-saves sont exclus de la liste parce que, même si f écrit
dedans, elle doit les rendre dans l’état où elle les a trouvés, ce qui
vu de l’extérieur revient à ne pas écrire dedans.
Il en va de même pour tous les autres temporaires, car la sémantique
des temporaires ordinaires est de ne pas être concernés par l’appel de
fonction (section 6.2.2).
Il faut bien comprendre que nous sommes justement en train de réaliser
cette sémantique.
Elle est à voir comme une donnée qui aide à comprendre
comment le sélecteur réalise les conventions d’appel.
En fait, les sources et les destinations des instructions sont une information destinées à l’analyse de durée de vie (liveness) préalable à l’allocation des registres. De son point de vue, les sources sont des temporaires nécessaires à l’exécution d’une instruction et les destinations sont les temporaires dont cette execution détruit le contenu. Ou plus exactement, comme cette information ne peut être totalement connue, les sources comprennent au moins les temporaires nécessaires et les destinations au moins les temporaires détruits. Adopter ce point de vue dès maintenant aide à comprendre les « lus » et les « ecrits » du type Ass.instr.
Les primitives sont un cas particulier, elles sont réalisées par de petites fonctions écrites en assembleur qui effectuent au final les appels système (qui bizarrement ne détruisent aucun registre, même pas ra) On connaît donc exactement les registres utiles et détruits de ces fonctions. Il convient de profiter de ce cas particulier. Par exemple, voici le source assembleur de la primitive alloc :
| sw $a0, 0($fp) sll $a0, $a0, 2 addu $v0, $fp, 4 addu $fp, $v0, $a0 j $ra |
La sous-routine alloc renvoie dans v0 l’adresse d’une zone de a0 mots de mémoire allouée dynamiquement. Le registre fp est réservé pour servir de pointeur vers la zone de mémoire encore libre. L’examen du code révèle que la sous-routine alloc lit le registre a0 et écrit dans les registres a0 et v0. Notons au passage que fp est réservé, c’est à dire que le code produit ne peut pas l’utiliser, il est donc totalement ignoré. Nous confions désormais le soin de determiner les registres détruits par une sous-routine à une fonction trash qui prend une fonction (un frame) en argument et renvoie la liste des registres potentiellement détruits par cette fonction. Nous nous livrons ici à un comportement de gagne-petit. Dans un compilateur normal, on peut éviter ce genre de suppositions peu rénumératrices et dangereuses (si on réécrit un bout d’assembleur).
Si la fonction f a plus de quatre arguments l’appelant doit empiler les arguments en excès. Pour simplifier supposons plutôt que seul le premier argument est passé en registre et que f a trois arguments. Rappelons que le frame de l’appelant de f s’étend de son frame-pointeur au pointeur de pile (registre sp). Si le frame-pointer reside dans un registre fp, l’appelant est libre de modifier sp, il se contente donc d’empiler les paramètres effectifs. Mais nous avons reservé fp pour un autre usage. Qu’à cela ne tienne, nous devons ranger les deuxième et troisième arguments au sommet de la pile, et nous pouvons donc nous repérer par rapport à sp. Mais pour être bien sûrs de ne rien écraser d’important à cette occasion, nous devons signaler à tout le back-end que le sélecteur a besoin de deux mot au sommet de la pile. On opère en avertissant le frame de l’appelant qui doit donc être passé en argument à emit_call (et donc aussi à emit_stm qui appelle emit_call).
let emit_store_sp_offset o t = emit (Oper ("sw ^s0,"^string_of_int o^"($sp)", [t], [], None)) let emit_call_1_2 caller_frame f e1 e2 e3 = emit_move_to a0 (emit_exp e1) ; emit_store_sp_offset 0 (emit_exp e2) ; emit_store_sp_offset 4 (emit_exp e3) ; Frame.make_space_for_args caller_frame 2 ; ...
La fonction make_space_for_args enregistre la demande en ajustant
la taille du sommet du frame de l’appelant en conséquence
(il se souvient de la demande maximale). On note donc au passage que
le type frame définit une structure de donnée légèrement
impérative.
La figure 7.10 résume la situation, à la sélection des appels de fonction nous sommes en train de calculer la taille de la zone des paramètres sortants, zone à allouer au sommet du frame de l’appelant. La taille de la zone des locaux, à allouer au fond du frame, sera calculée par l’allocation de registres. La taille totale du frame, size, ne sera donc connue que tout à la fin de la compilation.
La sélection des instructions du corps d’une fonction s’opère normalement, en itérant emit_stm. Le gros morceau est l’insertion du prologue au début et de l’épilogue à la fin (voir section 6.3.3). Programmatiquement nous avons donc :
| let emit_fun f body = (* f est le frame *) let saved_callees = emit_prolog f in List.iter (fun i -> emit_stm f i) body ; emit_epilog f saved_callees ; Table.trim_to_list my_table |
Prologue et épilogue réalisent notre modèle de gestion des environnements des fonctions. Le prologue commence par l’étiquette du point d’entrée de la fonction f. Il procède succesivement aux opérations suivantes :
Pour l’épilogue, qui commence par son étiquette (connue de la structure frame représentant f) la repose est à l’inverse de la dépose, selon la formule irritante de la Revue technique automobile.
Les étapes 3 du prologue et 1 de l’épilogue sont logiques, elles assurent l’indépendance de la génération de code intermédiaire vis à vis de du processeur ciblé. Elle ne posent qu’un léger problème technique dans le cas des arguments en excès passés en pile.
Les étapes 2 du prologue et de l’épilogue sont plus troublantes. Pour les réaliser l’émetteur du prologue renvoie la liste des sauvegardes des callee-saves qui est donnée en argument à l’émetteur de l’épilogue. La fonction f a la responsabilité de rendre les callee-saves dans l’état où elle les a trouvés. Le fonctionnement du processeur ne garantit rien à ce sujet, puisque toute écriture dans un registre est visible de partout. Mais la sémantique des temporaires garantit qu’un temporaire reste insensible aux appels de fonctions que f peut effectuer. Donc, comme le code de f se gardera bien de toucher aux sauvegardes des callee-saves, la combinaison de l’étape 2 du prologue et de l’étape 2 de l’épilogue garantit que f fait face à ses responsabilités. Soit s0 un callee-save, en pratique on s’attend à l’un où à l’autre des scénarios suivants.
L’allocateur de registres se dénommerait donc moins publicitairement, allocateur de registres ou de cases de piles.
Reste enfin la dernière étape 4 de l’épilogue. L’emission de l’instruction de retour d’une fonction qui rend son résultat dans v0 se fait ainsi :
| emit (Oper "j $ra", v0::callee_save_registers, [], Some []) |
(Pour une procédure les temporaires sources de l’instruction de retour ne comprennent pas v0)
On remarque d’abord que les sauts indiqués sont Some [], ce qui signifie qu’il y a bien saut mais que la destination est inconnue. L’instruction de retour lit effectivement le seul registre ra qui est inclus dans la liste des calle-saves. Et il est assez logique de considérer que f doit présenter à sa dernière instruction le registre ra dans l’état où elle l’a trouvé.
Mais du point de vue de l’usage qui peut être fait des registres machine, l’instruction de retour remplace toutes les instructions qui peuvent suivre au cours de l’exécution. Or, la suite du code de l’appelant peut selon les conventions d’appel lire v0 et les (vrais) callee-saves en toute confiance. Plus précisément, l’appelant doit, quand il lira ces registres, y trouver ce qu’il croit qu’ils contiennent, à savoir le resultat de l’appel pour v0 le cas échéant, et un contenu inchangé pour les callee-saves. Les autres registres (arguments et caller-saves) ne sont pas un problème car l’appelant sait toujours selon ces mêmes conventions que leur contenu n’est plus fiable. (voir les registres « écrits » par l’instruction d’appel).
Enfin, on peut aussi inclure les registres spéciaux (genre zero, sp, etc.) dans la liste des sources de l’instruction de retour. Je n’en voit pas trop l’intérêt, car ces registres sont réservés c’est à dire que leur usage n’est pas contrôlé selon le mécanisme général des temporaires lus et écrits par les instructions d’appel et de retour de sous-routine. Par exemple, l’usage correct du registre sp est garanti par la les diminutions et augmentations symétriques du prologue et de l’épilogue
L’allocation et la libération du frame de f (étapes 1 du prologue et 3 de l’épilogue) posent seulement un problème technique : la taille du frame ne sera connue qu’en aval, après l’allocation de registres. Nous pourions laisser des trous dans le code et aller les remplir ensuite (technique connue sous le nom de back-patching).
f_size = 12 # mis là après l'allocation de registres # Code produit par le sélecteur f: # prologue de f subu $sp, $sp, f_size ... f_end: # épilogue de f ... addu $sp, $sp, f_fize j $ra
Mais l’assembleur nous autorise une solution moins compliquée à mettre en œuvre. En effet, le programme qui s’appelle assembleur comprend souvent les constantes symboliques, c’est à dire les définitions de noms quelconques comme des entiers. Lorsque la taille de f sera connue (par exemple 12 octets), on pourra insérer une définition du nom f_size dans le code assembleur. Mais pour l’heure nous nous contentons d’utiliser ce nom (figure 7.11). Dans le cas où f_size se révèle finalement nul on peut souhaiter supprimer les instructions d’ajustement du pointeur de pile. Oublions ce détail.
Il reste à examiner le passage d’arguments en pile.
Supposons que f prend trois arguments, dont le premier est passé en
registre et les deux suivants en pile.
Les arguments sont récupérés après l’allocation du frame
(étape 1 du prologue), c’est à dire que le pointeur de
pile est déjà diminué de f_size, taille du frame de f.
Ici encore, on peut désigner la position en pile des arguments
entrants en s’aidant de la constante symbolique f_size
(figure 7.12).
En supposant un unique vrai callee-save s0, le code d’émission du prologue f est donné par la figure 7.13.
let emit_load_arg d o = emit (Oper "lw ^d0,"^o^"($sp)", [], [d], None) let emit_prolog_1_2 f = let f_size = Gen.label_string (Frame.frame_label f)^"_size" in (* point d'entrée et allocation du frame *) emit_label (Frame.frame_label f) ; emit (Oper ("subu $sp, $sp, "^f_size, [], [], None)) ; (* sauvegarde des callee-saves *) let saved_ra = new_temp () and saved_s0 = new_temp () ; emit_move saved_ra ra ; emit_move saved_s0 s0 ; (* récupérer les arguments *) let [t1 ; t2 ; t3] = Frame.frame_args f in emit_move t1 a0 ; emit_load_arg t2 ("0+"^f_size) ; emit_load_arg t3 ("4+"^f_size) ; (* rendre les sauvegardes des callee-saves, pour l'épilogue *) [saved_ra ; saved_s0]
Bien sûr, dans le sélecteur que vous allez écrire, vous devez écrire
une fonction emit_prolog générale qui traite le cas de toutes
les fonctions, quelque soit leur nombre d’arguments.
Soit la fonction facorielle écrite en Pseudo-Pascal.
| function fact (n : integer) : integer; begin if n <= 1 then fact := 1 else fact := n * fact (n - 1) end ; |
Le code intermédiaire généré est le suivant :
function fact args = $t105 result = $t104 Cjump L12 L13 (<= $t105 1) L13: (set $t107 $t105) (set $t106 (call fact (- $t105 1))) (set $t104 (* $t107 $t106)) Jump fact_end L12: (set $t104 1)
Dans le code assembleur produit par le sélecteur (en se donnant un seul callee-save s0), on notera particulièrement l’apparition du prologue et de l’épilogue.
|
|
Il y a de nombreux temporaires et transferts entre temporaires qui sembleraient gréver l’efficacité finale du code. Mais le compilateur peut très bien au final produire ce code :
|
|
Dans ce code final, les temporaires $111 et
$112 se retrouvent en pile.
On note que les temporaires argument
($105) et résultat ($104) se retrouvent respectivement dans les
registres argument (a0) et résultat (v0), ainsi que
l’allocation du registre s0 au temporaire $107 qui
est à la racine de la bonne allocation des registres.
Nous avons pris soin de selectionner les instructions « immédiates »
(c’est à dire celles qui prennent une seconde source qui est un entier
sur 16 bits) dès que c’était possible et ceci pour toutes les
instructions qui opèrent sur un mode trois adressses. Or, une étude
attentive du jeu d’instructions du processeur MIPS (et non de toutes
les instructions acceptées par l’assembleur) révèle que parmi les
instructions qui nous intéressent, les seules qui peuvent prendre une
deuxième source immédiate sont en fait
add, addu, slt (opération <),
sll et sra (décalages). Mais, l’assembleur
sait traiter toutes les instructions immédiates que nous
sélectionnons, dans le cas de la soustraction il saura même remplacer
une soustraction immédiate inexistante en machine par l’addition
immédiate équivalente (sauf si la constante est −(215)
…). Dans le cas général l’assembleur remplacera l’instruction
immédiate par un chargement préalable dans l’un de ses deux registres
réservés et l’instruction trois-adresses correspondante. Nous pouvons
donc sans nous fatiguer sélectionner toutes ces instructions
immédiates, nous aurions même pu nous éviter de verifier que
l’argument entier tient sur 16 bits, Mais tous les assembleurs ne sont
pas aussi sympathiques.
Toutefois il est un cas où nous devons travailler nous mêmes, il
s’agit de la multiplication et de la division.
Ces instructions prennent plus de temps à exécuter que les autres
et il convient, quand le deuxième argument est constant de tenter de
les remplacer par une ou plusiseures instructions « normales ».
C’est particulièrement important dans le cas des multiplications
par la taille naturelle du mot introduites à foison par les accès dans
les tableaux.
Or, une multiplication par 2b est équivalente à un décalage à gauche
de b positions (sll), tandis
qu’une division (signée) par 2b est équivalente à un décalage dit
arithmétique à droite de b
positions (sra).
Dans ce dernier type de décalage, le bit de signe (le plus à droite) est
répliqué b fois afin de combler le trou laissé par le décalage.
Bref, on peut, grâce au repérage effectué par emit_exp, traiter
quelques cas particuliers fréquents et significatifs dans
emit_binop (cf. figure 7.7).
and emit_binop op e1 = function | Const i -> let s = emit_exp e1 and d = new_temp () in (* selection ad-hoc pour quelques cas importants *) begin match op,i with | Times,2 -> emit_sll d s 1 | Times,4 -> emit_sll d s 2 | Div, 2 -> emit_sra d s 1 | Div, 4 -> emit_sra d s 2 | _,_ -> emit_op2 op d s i end ; d | e2 -> let s0 = emit_exp e1 and s1 = emit_exp e2 and d = new_temp () in emit_op3 op d s0 s1 ; d
Idéalement, une transformation aussi simple, revenant à remplacer une opération coûteuse (une multiplication) par une autre certainement moins coûteuse (un décalage), est valable pour tous les processeurs, et on aurait du y procéder en amont. Des réductions plus ambitieuses sont possibles, c’est à dire que l’on peut transformer une multiplication par une constante en k instructions. Mais on retrouve alors un problème de dépendance au processeur, notamment pour connaître la limite supérieure de k en fonction des coût des instructions. On notera aussi que ce type de transformation profitera surtout aux programmes qui font beaucoup de multiplications, et non pas à tous les programmes en général. On ne s’attaquera donc à cette optimisation que si le besoin s’en fait sentir.
Les processeurs Intel se distinguent par leur jeu d’instruction moins régulier que celui du MIPS (d’où plus de tuiles) et aussi par leurs opérations « deux-adresses ».
Ainsi, une addition s’écrit :
| addl r2, r1 # r1 ← r1 + r2 |
(Attention à l’inversion des arguments !). Ce n’est pas réellement une difficulté, il suffit de continuer à considérer les opération comme « trois adresses » (genre t1 ← t2 + t3) et d’emettre le code :
| movl t2, t1 # t1 ← t2 addl t3, t1 # t1 ← t1 + t3 |
On compte sur l’allocateur de registres pour attribuer si possible le même registre machine aux temporaires t1 et t2.
Dans les anciens processeurs Intel, l’instruction de multiplication est très contrainte. Le multiplicateur est nécessairement dans %eax, et le résultat est sur 64 bits, poids faibles dans %eax et poids forts dans %edx. Pour réaliser une multiplications trois-adresses t1 ← t2 * t3, on émettra :
| movl t2, %eax # %eax ← t2 imull t3 # %eax ← %eax * t3, %edx ← ? movl %eax, t1 # t1 ← %eax |
Et surtout ou oubliera pas %edx dans la liste des temporaires « écrits » par l’instruction imull. Ici encore on peut espérer une allocation des temporaires t1 et t2 dans le registre %eax, mais c’est faire preuve d’optimisme. Dans les processeurs Intel plus modernes, on a une multiplication deux adresses, mais le problème demeure pour la division.
La majorité des opérations peut aussi opérer en mémoire. Ainsi on peut écrire :
| addl t2, 4(t1) # [4+t1] ← [4+t1] + t2 |
L’effet est d’additionner t2 au contenu de la case mémoire adressée par 4+t1. Il n’y a pas de problème majeur pour identifier la tuile associée si le code intermédiaire exhibe ce motif et de toute façon ce sera un cas bien rare (incrément d’une case de tableau). Mais si les accès mémoire résultent de la mise en pile d’un temporaire en pile (mise en pile décidée après la sélection), on aura plutôt ce style de code :
| movl 4(%esp), t # t ← [4 + %esp] addl t2, t # t ← t + t2 movl t, 4(%esp) # [4 + %esp] ← t |
Ce n’est en fait pas bien grave car ce second code a un temps d’exécution théorique identique au premier code en une instruction. La pénalitée payée est un code un peu moins compact et un temporaire en plus (t), qui compte tenu de sa durée de vie très courte sera alloué en registre.
Enfin on peut souhaiter exploiter les instructions d’empilage et de dépilage qui on un effet de bord (décrément ou incrément de la taille du mot) sur le registre %esp.
| pushl t # %esp ← %esp − 4 ; [0 + %esp] ← t popl t # t ← [0 + %esp] ; %esp ← %esp + 4 |
On peut, pour un léger gain en vitesse, employer ces instructions de façon ad-hoc. Je pense surtout à l’empilage des arguments en excès lors des appels de fonction. Cela n’a en fait aucun intérêt dans le cas de notre compilateur qui regroupe les mouvements du pointeur de pile dans le prologue et l’épilogue. C’est un peu plus pertinent dans le cas d’un frame-pointeur en registre.


