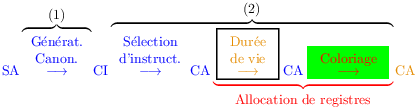



La mission de l’allocation de registres est de transformer les temporaires arbitraires du code assembleur produit par la sélection (voir le chapitre 7) en registres de la machine ciblée. Grâce à l’analyse de durée de vie, chapitre 8 il est relativement facile d’obtenir que les contenus des temporaires ne se mélangent pas, c’est à dire d’obtenir du code correct au final.
Malheureusement, il est parfois impossible de réaliser un temporaire à l’aide d’un registre machine, il faut alors réaliser le temporaire en pile, c’est à dire lui allouer non plus un registre machine, mais une case mémoire en pile. Le but d’une bonne allocation de registres est de minimiser le nombre de temporaires alloués en pile. Un but secondaire est de minimiser les transferts entre registres. En effet si le code assembleur comprend une instruction de transfert entre deux temporaires t1 et t2, on a alors intérêt (si c’est possible) à allouer le même registre à t1 et t2, afin d’éliminer l’instruction de transfert.
Nous sommes donc tout à la fin de chaîne de compilation. Par ailleurs le bon emploi des registres est crucial pour l’efficacité du code produit par le compilateur. Pour ces deux raisons la phase d’allocation de registres est sans doute la plus connue des phases du back-end. Et de fait, la majorité des bizarreries rencontrées lors des phases précédentes trouvent maintenant leurs explications.
Dans ce cours je vais décrire l’allocation de registre par coloriage de graphe.
Avant d’entrer dans le vif du sujet, commençons par examiner pourquoi nous sommes sûrs de produire du code exécutable au final.
Considérons un bout de code quelconque encore paramétré par deux temporaires.
| add t1, t2, 2 mul t1, t1, t2 |
Décidons d’allouer t1 et t2 en pile (to spill. mot
anglais que je vais utiliser comme synonyme de « allouer un temporaire
en pile »).
Il suffit d’adresser cette demande au frame de la fonction en cours
de compilation (voir la section 6.3.3) à l’aide de la
fonction idoine (Frame.alloc_local) qui alloue et renvoie une
position en pile repérée par rapport au pointeur de pile.
De fait nous allouons maintenant la zone des locaux du frame, voir la
figure 7.10.
Donc ici, supposons que t1 dans la première case de pile (indice 0) et t2 dans la deuxième (indice 4). Il faut maintenant réécrire le code pour ajouter autour des opérations des lectures et écritures en mémoire dans et vers des registres dits auxiliaires de spill. Pour le moment, supposons que nous disposons de deux registres machine réservés à cet usage, t8 et t9.
| lw $t8, 4($sp) # load t2 add $t8, $t8, 2 sw $t8, 0($sp) # store t1 lw $t8, 0($sp) # load t1 lw $t9, 4($sp) # load t2 mul $t8, $t8, $t9 sw $t8, 0($sp) # store t1 |
Le code n’est pas très bon, mais nous nous débrouillerons, d’abord pour éviter le plus possible d’allouer en pile et ensuite pour bien choisir les temporaires spillés.
Dans notre compilateur un module spécifique Spill est chargé de l’allocation en pile et de la réécriture du code, son interface est donnée par la figure 9.1.
val spill_fun : Ass.temp Smallset.set -> Spim.procedure -> Spim.procedure (* « spill_fun temps proc » renvoie une procédure modifiée : les temporaires de temps sont alloués en pile. *)
En spillant tous les temporaires d’un code donné, on obtient donc un code assembleur exécutable et correct. C’est exactement ce que fait l’option -spill du compilateur du cours.
Rappelons que les sommets du graphe d’interférence sont les temporaires, et que les arcs expriment que deux temporaires reliés ne peuvent pas résider au final dans le même registre.
Allouer des registres aux temporaires revient à colorier le graphe d’interférence, c’est à dire à assigner des couleurs aux sommet de sorte que deux sommets reliés sont de couleurs différentes. Posé dans toute sa généralité le coloriage de graphe est NP-complet. Heureusement il existe un algorithme simple (et linéaire) permettant de colorier un graphe avec K couleurs.
Soit donc un graphe G, et K couleurs. Par définition, les sommets de G se répartissent en sommets de faible et de fort degré, c’est à dire qui possèdent strictement moins de K voisins, ou K voisins ou plus. L’algorithme, connu depuis le 19ième siècle, repose sur l’observation suivante : si le graphe G possède un sommet s de faible degré, et que le graphe G−{s} est K-coloriable, alors G est K-coloriable. Mieux, si on a su effectivement colorier les sommets de G−{s}, alors on sait colorier s : il suffit de choisir pour s une couleur différente de celle de tous ses voisins.
On déduit facilement un algorithme récursif de l’observation. Dans une première phase de descente on retire un sommet de faible degré de graphe, cette opération pouvant changer des voisins de degré K en sommets de faible degré. Puis, dans une phase de remontée (après un appel récursif), on colorie le sommet retiré du graphe à la descente. L’algorithme proposé est incomplet, c’est à dire qu’il peut échouer alors que le graphe est K-coloriable. Ce n’est pas très gênant en pratique :
Pour fixer les idées, nous allons immédiatement coder l’algorithme en Caml. Il n’est ni pratique, ni efficace d’effectivement enlever des sommets (et des arcs) au graphe en cours de coloriage. À la place, nous allons plutôt répartir les sommets entre les divers sous-ensembles d’une partition des sommets. Le module Partition (cf. figure 9.2) fournit une réalisation impérative des partitions.
(* Ce module fournit des opérations efficaces sur un ensemble partitionné en un nombre fixe de sous-ensembles. *) type 'a t (* type des sous-ensembles de la partition *) type 'a elem (* type des éléments *) val make : int -> 'a t array (* make n créer un vecteur de partitions *) val clear : 'a t -> unit (* clear s efface la partition s e *) val create : 'a t -> 'a -> 'a elem (* « create s e » créer un élément e dans le sous-ensemble s *) val info : 'a elem -> 'a (* « info e » retourne les informations sur l'élément e *) val belong : 'a elem -> 'a t -> bool (* test d'appartenance *) val move : 'a elem -> 'a t -> unit (* changement de sous-ensemble *) val pick : 'a t -> 'a elem option (* « pick s » renvoie un élément de s, None si s est vide *) val pick_lowest : ('a elem -> float) -> 'a t -> 'a elem option (* « pick_lowest cost s » renvoie un élément de s de coût minimal, None si s est vide *) val list : 'a t -> 'a elem list (* renvoie la liste des éléments d'un sous-ensemble *)
Nous commençons par nous donner une partition en quatre sous-ensembles :
| let sets = Partition.make 4 let precolored = sets.(0) and low = sets.(1) and high = sets.(2) and removed = sets.(3) |
Les sommets de G se répartiront donc entre sommets déjà coloriés (les registres machine), sommets de faible et fort degré, et sommets enlevés du graphe en attente de coloriage.
Rappelons ensuite la définition des informations associées aux sommets du graphe d’interférence.
| (* Contenu des noeud du graphe d'interférence *) type interference = { temp : temp; (* un temporaire *) (* Les champs suivants sont utiles pour l'allocation de registres *) mutable color : temp option ; mutable degree : int ; mutable elem : ((interference Sgraph.node) Partition.elem) option ; mutable occurs : int ; } |
Pour le moment, nous nous intéressons aux champs temp
(le temporaire à colorier), color
(une option de temporaire qui sera la couleur),
degree (le degré courant du sommet), et elem.
Supposons qu’une phase initiale non décrite ajuste les champs
color (None pour un « vrai » temporaire et
Some r pour un registre machine r),
et degree (en comptant tout bêtement les voisins).
Nous pouvons alors répartir initialement les sommets dans la
partition :
| (* Mach.registers est la liste des registres machines *) let colors = Smallset.of_list Mach.registers and ncolors = List.length Mach.registers let ig_info ig n = Sgraph.info ig n let build_partition ig = Sgraph.iter ig (fun n -> let i = ig_info ig n in let e = match i.color with | Some r -> Partition.create precolored n | None -> if i.degree < ncolors then Partition.create low n else Partition.create high n in i.elem <- Some e) |
Notez que pour une raison qui apparaîtra par la suite, le sommet lui-même est enregistré en tant qu’élément de la partition dans le champ elem. C’est un détail d’implémentation.
En effet, lorsque l’on retire un sommet du graphe, il faut aussi enlever les arcs correspondants, ce qui revient, dans notre réalisation à diminuer le champ degree des voisins. Il convient alors, si le degré est passé sous la barre des K−1 de faire passer le voisin de high à low :
| let decr_degree ig e = (* e est un élément de partition *) let n = Partition.info e in (* sommet du graphe *) let i = Sgraph.info ig n in (* informations associés au sommet *) if Partition.belong e low || Partition.belong e high then begin i.degree <- i.degree-1 ; if i.degree = ncolors-1 then Partition.move e low end |
La fonction suivante remove enlève donc un sommet du graphe ig en oubliant pas de décrémenter les degrés de ses voisins.
| let elem_of_node ig n = match info_ig ig n with | {elem=Some e} -> e | _ -> assert false let remove ig e = let n = Partition.info e in let adjs = Sgraph.adj ig n Inter in List.iter (fun n -> decr_degree ig (elem_of_node ig n)) adjs ; Partition.move e removed |
Une fois tous les sommets « enlevés », nous les colorions un
par un, dans l’ordre inverse (dernier enlevé en premier).
Pour ce faire nous avons besoin d’une fonction adj_color qui
donne les couleurs des voisins d’un sommet, utilisée par une fonction
choose_color qui choisit une couleur arbitraire parmi les
couleurs qui ne sont pas des couleurs de voisins.
Cette dernière fonction utilise Smallset.choose qui prend un
ensemble en argument et renvoie un élément arbitraire de cet ensemble
comme une option, ou qui renvoie None si l’ensemble est vide.
| let adj_colors ig e = let n = Partitition.info e in let adjs = Sgraph.adj ig n Inter in Smallset.union_list (List.map (fun n -> match ig_info ig n with | {color=Some r} -> Smallset.singleton r | {color=None} -> Smallset.empty) adjs) let choose_color ig e = let forbiden = adj_colors ig e in Smallset.choose (Smallset.diff colors forbiden) |
Notez bien que les voisins qui n’ont pas de couleurs (champ color à None) sont ceux qui ont été « enlevés » avant le sommet colorié et qui donc seront coloriés ensuite.
Nous sommes maintenant équipés pour colorier le graphe d’interférence. La fonction colorize (figure 9.3) colorie le graphe par effet de bord et renvoie un booléen qui dit si elle a pu mener sa tâche à bien.
let put_color ig e c = let n = Partition.info e in let i = ig_info ig n in i.color <- c let rec colorize ig = match Partition.pick low with | Some e -> (* prendre un sommet de faible degré *) remove ig e ; (* « l'enlever » *) if colorize ig then begin (* colorier le reste du graphe *) let c = choose_color ig e in (* colorier le sommet enlevé *) put_color ig e c ; true end else false | None -> (* low est vide *) match Partition.pick high with | Some _ -> false | None -> true
Notons que, lors de la remontée, le coloriage ne peut échouer, c’est à dire que choose_color renvoie toujours bien une couleur (ne renvoie jamais None). L’échec ne peut survenir que lors de la descente, quand il n’y a plus de sommets de faible degré et encore au moins un sommet de fort degré.
Considérons le fonctionnement de notre algorithme simple sur le graphe d’interférence de la section 8.2. En fait, le graphe colorié est un peu différent. D’une part, nous ajoutons un second sommet précolorié, a0, en plus de v0, afin de clairement montrer que le coloriage s’effectue à l’aide de deux registres. D’autre part les arcs move subissent la fermeture décrite à la fin du chapitre précédent, ce qui revient ici à ajouter un arc pointillé entre r et v0.
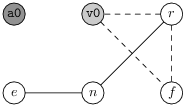
Allouer des registres aux quatre temporaires, revient donc ici à colorier ces quatre sommets du graphe d’interférence à l’aide des deux couleurs des sommets qui sont déjà des registres (gris foncé et gris clair). Initialement nous avons deux sommets déjà coloriés (a0 et v0), trois sommets de faible degré (e, f et r) et un sommet de fort degré (n). La figure 9.4 décrit l’exécution des deux phases de l’algorithme. Lors de la descente la partition des sommets est montrée. Lors de la remontée, la couleur choisie est montrée.
low high removed e, f, r n f, n, r e n, r e, f r e, f, n e, f, n, r
sommet interdit possible choisie r a0, v0 a0 n a0 v0 v0 f a0, v0 v0 e v0 a0 a0
On remarquera que lors de la descente, enlever le sommet e fait passer son voisin n dans les sommets de faible degré. Au retour le choix des couleurs est arbitraire, pour r et f et forcé pour n et e. Le choix fait ici ne tient pas compte des arc move, une allocation plus pertinente résulterait d’un premier coloriage de r en v0, mais nous y reviendrons.
Observons maintenant la situation qui mène à l’échec de l’algorithme simple : le graphe est non-vide et tous ses sommets sont de fort degré. Selon le schéma simple, nous ne pouvons plus rien faire, il convient alors de simplifier le graphe en spillant quelques temporaires et de tenter un coloriage du graphe ainsi simplifié. Toutefois, rien ne nous dit que le graphe n’est pas K-coloriable, nous pourrions très bien choisir un sommet s (représentant le temporaire t) de fort degré, « l’enlever » du graphe et continuer.
Dès lors, en phase de remontée du coloriage, on aura deux possibilités :
Dans le premier cas, s n’empêche pas en fait de colorier le graphe, dans le second, il convient d’allouer t en mémoire, c’est à dire de le spiller. En raison de la seconde possibilité, le temporaire choisi parmi les sommets de fort degré s’appelle un spill potentiel (potential spill).
On notera que si les auxiliaires de spill sont réservés (cf. section 9.1) alors on peut continuer la remontée, afin de terminer le coloriage du graphe d’interférence produit en enlevant les sommets spillés. Dans tous les cas, il convient de poursuivre la remontée afin d’identifier ceux des spills potentiels qui doivent effectivement être spillés.
Le choix du sommet s est critique et ceci pour deux raisons :
En pratique, on se donne une fonction de coût cost qui décroît avec le degré des sommets et croit avec le nombre d’occurences des temporaires dans le code (champ occur des informations du graphe d’interférence). Le moment venu, on choisit un sommet de coût minimum parmi les sommets de fort degré.
L’algorithme de coloriage optimiste est donné par la figure 9.5. Par rapport au coloriage simple de la figure 9.3, on note l’apparition de deux nouveaux sous-ensembles dans la partition des sommets du graphe d’interférence : colored pour les sommets finalement coloriés, et spilled pour les autres. À la remontée, on répartit les sommets de removed dans l’un ou l’autre de ces sous-ensembles, selon que leur coloriage est possible ou pas.
let sets = Partition.make 6 let precolored = sets.(0) ... and colored = sets.(4) and spilled = sets.(5) let cost ig e = ... let select_spill ig = Partition.pick_lowest (cost ig) high let rec colorize ig = match Partition.pick low with | Some e -> (* prendre un sommet de faible degré *) remove ig e ; (* « l'enlever » *) colorize ig ; (* colorier le reste du graphe *) begin choose_color ig e with (* choisir une couleur *) | Some c -> (* colorier *) put_color ig e (Some c) ; Partition.move e colored | None -> (* spiller *) Partition.move e spilled end | None -> (* low est vide *) match select_spill ig with (* selectionner un spill potentiel *) | Some e -> Partition.move e low ; colorize ig (* « l'enlever », continuer *) | None -> () (* graphe vide, c'est fini *)
On notera que le code comporte une astuce, les spills potentiels ne sont pas directement enlevés, mais bougés du sous-ensemble high vers low. L’astuce permet de n’insérer le code de coloriage qu’après le premier appel récursif à colorize.
Au retour de colorize on détectera la réussite ou l’échec en
regardant si spilled est vide ou pas.
Dans le premier cas on se livrera à un dernier passage sur le code
(remplacer les temporaires par leur couleur, émettre la définition de
la constante symbolique correspondant à la taille du frame). Dans le
second cas, il faut réécrire le code à l’aide de spill_fun
(figure 9.1) et tout recommencer.
En effet, notre compilateur alloue des temporaires frais comme auxiliaires de spill, temporaires qui peuvent interférer avec d’autres, ce qui commande de reconstruire un graphe d’interférence et de recommencer l’allocation de registres. Mais spiller un temporaire revient à transformer le graphe d’interférence en un autre « plus simple ». En effet les temporaires créés comme auxiliaires de spill ont une durée de vie très courte, on les appelle des éphémères. Par conséquence, le temporaire spillé est remplacé par une multitude de temporaires éphémères et les interférences diminuent. Par exemple, considérons l’exemple de la section 9.1 en utilisant cette fois des temporaires éphémères.
| lw e1, 4($sp) # load t2 add e2, e1, 2 sw e2, 0($sp) # store t1 lw e3, 0($sp) # load t1 lw e4, 4($sp) # load t2 mul e5, e3, e4 sw e5, 0($sp) # store t1 |
Si les temporaires t1 et t2 interféraient avec un troisième t3 en raison par exemple du code qui suit notre exemple, le temporaire t3 est maintenant moins contraint, puisqu’il ne peut interférerer avec les éphémères e1 à e5.
En pratique, on itère donc l’algorithme de coloriage de graphe sur des graphes d’interférence de plus en plus simples. L’expérience montre que le coloriage s’effectue après éventuellement une, plus rarement deux tentatives infructeuses, à condition de ne pas spiller les auxiliaires de spill. En effet :
En pratique on évite simplement le spill des auxiliaires de spill en
dotant les éphémères alloués par spill_fun d’un coût
exhorbitant.
En notant que les éphémères sont créés à l’aide d’une fonction idoine
(Gen.ephemere au lieu de Gen.new_temp) et que l’on peut
savoir si un temporaire est un éphémère (par la fonction
Gen.is_ephemere de type Gen.temp -> bool).
Nous pouvons essayer cette fonction de coût pour le
choix des spills potentiels parmi les sommets de fort degré :
| let cost ig e = let n = Partition.info e in let i = Sgraph.info ig n in (float i.occurs) /. (float i.degree) +. (if Gen.is_ephemere i.temp then 100.0 else 0.0) |
La fonction cost est bien croissante avec le nombre d’occurences, décroissante avec le degré et de coût exhorbitant pour les éphémères. Cette fonction peut être améliorée par des essais. En outre, si on dispose d’informations précises sur le contrôle du programme, on dotera les temporaires qui apparaissent dans les boucles d’un coût relativement élevé.
L’algorithme complet de coloriage peut être représenté graphiquement (figure 9.6). Dans cette représentation, la pile des sommets est explicitée, alors que dans le code récursif de la figure 9.5 cette pile était implicite. Cette pile est remplie lors de la descente et vidée lors de la remontée.
Jusqu’ici nous avons superbement ignoré les arcs move, ce qui fait que nous choisissons les couleurs un peu au hasard. Ainsi, la figure 9.7 donne (à droite) le code final produit pour l’exemple de la figure 8.1 (rappelé à gauche) à partir de l’allocation des couleurs obtenue à la figure 9.4.
li e, 1 ble n, e, L12 L13: li r, 1 b L16 L15: mul r, r, n sub n, n, 1 L16: bgt n, $zero, L15 L17: move f, r b fact_end L12: li f, 1 fact_end: move $v0, f
li $a0, 1 ble $v0, $a0, L12 L13: li $a0, 1 b L16 L15: mul $a0, $a0, $v0 sub $v0, $v0, 1 L16: bgt $v0, $zero, L15 L17: move $v0, $a0 b fact_end L12: li $v0, 1 fact_end: move $v0, $v0
Le dernier transfert entre registres (de v0 dans v0) est
inutile et peut être enlevé, mais il reste encore un transfert
(à l’étiquette L17).
En revenant sur le déroulement de l’algorithme (figure 9.4) nous voyons que l’attribution arbitraire du registre a0 au temporaire r est maladroite. En effet, les arcs move relient r f et v0, de sorte que l’attribution de v0 est désirable. Plus généralement nous pouvons definir les couleurs désirables d’un temporaire t comme celles des temporaires voisins de t selon les arcs move, et choisir pour t une couleur désirable quand c’est possible. Si, lors de la remontée nous choisisons des registres désirables, nous obtiendrons ici la meilleure allocation des registres possible, puisque tous les transferts entre registres disparaissent, comme indiqué par la figure 9.8.
sommet interdit desirable choisie r v0 v0 n v0 a0 f v0 v0 e a0 v0
li $v0, 1 ble $a0, $v0, L12 L13: li $v0, 1 b L16 L15: mul $v0, $v0, $a0 sub $a0, $a0, 1 L16: bgt $a0, $zero, L15 L17: # move $v0, $v0 b fact_end L12: li $v0, 1 fact_end: # move $v0, $v0
Mais ce n’est pas tout, donnons nous maintenant trois registres v0, a0 et a1. Le graphe d’interférence devient.
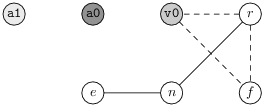
Tous les sommets du graphe d’interférence sont maintenant de faible degré, et le coloriage peut très bien commencer par exemple par le temporaire n. Ce temporaire ne possède pas de couleur désirable, puisqu’il n’a pas de voisins selon les arcs move. Pourtant, choisir pour lui le registre v0 est maladroit puisque nous rendons alors impossible l’attribution de la couleur v0 à r. Nous pouvons tenir compte de cet effet en définissant les couleurs indésirables d’un temporaire comme les couleurs désirables des temporaires qui interfèrent avec lui. Le choix des couleurs s’opère ensuite selon ce schéma :
En pratique on transforme facilement le colorieur de la figure 9.5 en un colorieur biaisé en changeant seulement la fonction choose_color. Ce petit codage est laissé en exercice.
Considérons cette fois le code complet (avec prologue et épilogue) de la fonction fact de la section 8.4.
| fact: subu $sp, $sp, fact_f move $111, $ra move $112, $s0 move $107, $a0 li $108, 1 b L13 L12: mul $108,$108,$107 sub $107, $107, 1 L13: bgt $107, $zero, L12 L14: move $106, $108 fact_end: move $v0, $106 move $ra, $111 move $s0, $112 addu $sp, $sp, fact_f j $ra |
Voici une animation du coloriage du graphe d’interférence de cette fonction, avec quatre registres. Si l’animation est à l’arrêt, vous pouvez la redémarrer en cliquant sur le bouton Reload de votre brouteur.
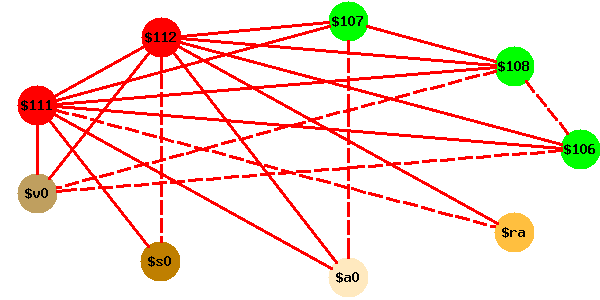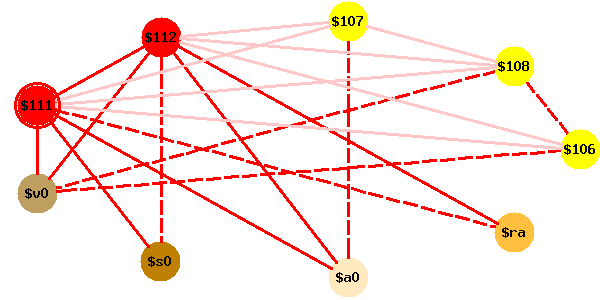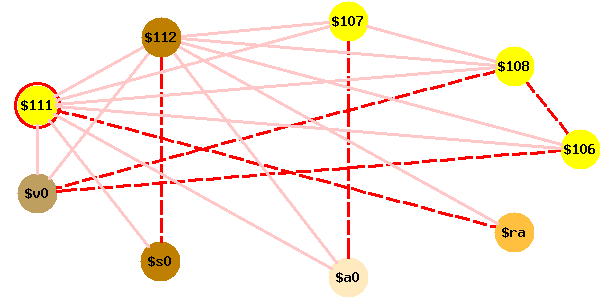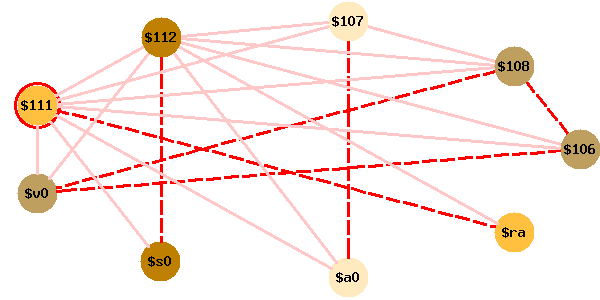
Les couleurs de l’animation se comprennent ainsi :
Quelques remarques peuvent aider à suivre l’animation.
$106,
$107 et $108, tandis que les temporaires de fort degré (rouges)
sont $111 (sauvegarde de ra) et $112 (sauvegarde
de s0).
$111
et $112 sont de degré 4, car ils interfèrent avec trois
registres et entre eux.
$111 est choisi comme spill potentiel
(il est cerclé de rouge) et « enlevé » du graphe (il passe en jaune).
$111 fait de $112 un sommet de faible
degré ($112 passe en vert).$112 est d’abord colorié par
sa couleur désirée s0.
$111 ne soit spillé, mais il n’en est rien car
deux de ses quatre voisins ($112 et s0) sont de même
couleur. En conséquence, on peut attribuer sa couleur désitable
ra à $111.
L’execution présentée donne donc un exemple de succès de la stratégie
optimiste de coloriage.
$108 ne provient pas d’un transfert présent dans le code, mais
de la fermeture des transferts de $108 vers $106 et de
$106 vers v0.
Au final l’algorithme optimiste parvient à colorier le graphe :
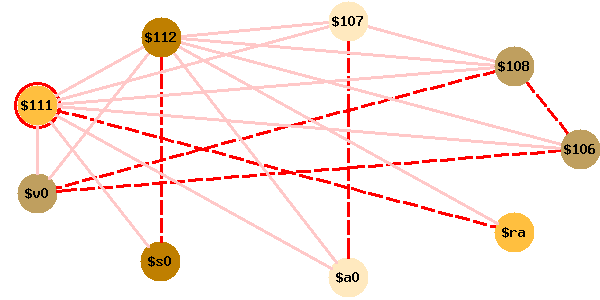
Ce qui donne le code exécutable suivant :
| fact: li $v0, 1 b L13 L12: mul $v0,$v0,$a0 sub $a0, $a0, 1 L13: bgt $a0, $zero, L12 j $ra |
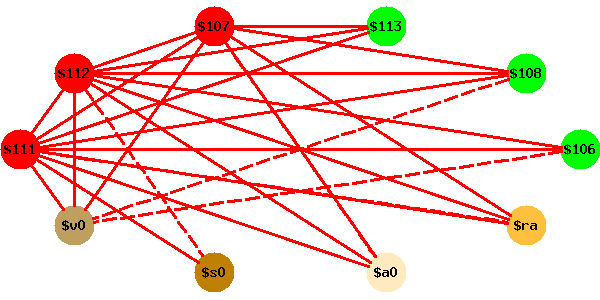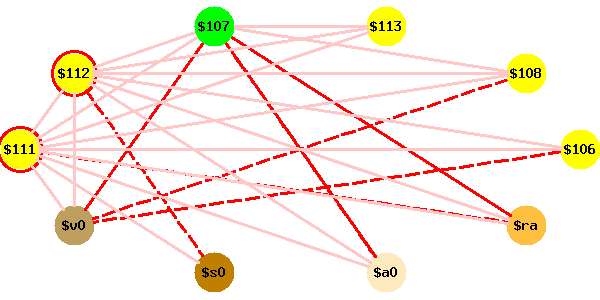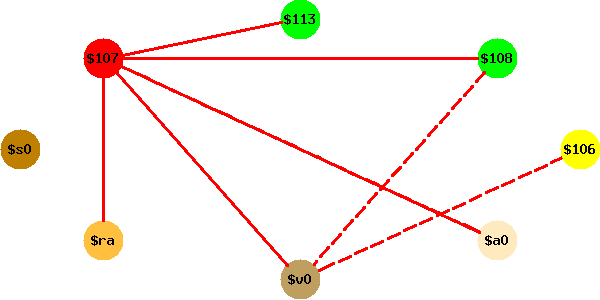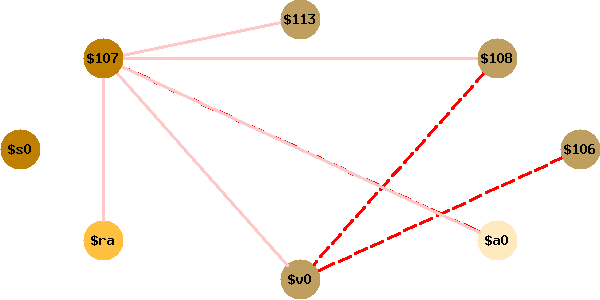
Je ne resiste pas au plaisir de donner un deuxième exemple d’exécution de l’algorithme de coloriage, avec cette fois le spill de deux registres. Il s’agit de la fonction factorielle récursive compilée à l’aide de quatre registres.
| fact: subu $sp, $sp, fact_f move $111, $ra move $112, $s0 move $107, $a0 li $113, 1 ble $107, $113, L12 L13: sub $a0, $107, 1 jal fact # $v0 $a0 $ra move $108, $v0 mul $106,$107,$108 b fact_end L12: li $106, 1 fact_end: move $v0, $106 move $ra, $111 move $s0, $112 addu $sp, $sp, fact_f j $ra |
Il faut ici se livrer à deux coloriages, le premier identifiant les
deux temporaires à spiller ($111 et $112), le second
coloriant le graphe simplifié.
On note qu’ici les temporaires spillés ne participent qu’à des
tranferts entre temporaires (ce sont les sauvegardes des
callee-saves ra et s0). Par conséquent le graphe
d’interférence simplifié est simplement le graphe de départ moins les
sommets des temporaires spillés.
Ici encore le code final n’est pas mauvais.
| fact_f=8 fact: subu $sp, $sp, fact_f sw $ra, 0($sp) # store $111 sw $s0, 4($sp) # store $112 move $s0, $a0 li $v0, 1 ble $s0, $v0, L12 sub $a0, $s0, 1 jal fact # $v0 $a0 $ra mul $v0,$s0,$v0 b fact_end L12: li $v0, 1 fact_end: lw $ra, 0($sp) # load $111 lw $s0, 4($sp) # load $112 addu $sp, $sp, fact_f j $ra |
Cet exemple illustre assez bien un effet de l’adoption de la
convention callee-save.
Le spill, peu coûteux, de la sauvegarde $112 libère le
registre callee-save s0. Ce registre devient alors disponible pour le temporaire très
contraint $107. On obtient donc un code acceptable, même si notre technique de spill est
un peu simpliste.

