Chapitre 4 Analyse lexicale

L’analyse lexicale se trouve tout au début de la chaîne de compilation, elle collabore avec l’analyse grammaticale pour passer de la syntaxe concrète à la syntaxe abstraite. La mission de l’analyse lexicale est de transformer une suite de caractères en une suite de mots, dit aussi lexèmes (tokens). Procéder ainsi en deux temps, en reconnaissant d’abord les mots, puis les phrases, n’est pas justifié par la théorie. En effet, un analyseur grammatical est strictement plus puissant qu’un analyseur lexical et il pourrait reconnaître les mots. La justification est pratique, l’analyseur grammatical est bien plus facile à écrire une fois les mots reconnus.

4.1 Enjeux

La production d’un arbre (de syntaxe abstraite) à partir d’une suite de caractères se retrouve comme première passe dans de nombreuses applications (analyses des commandes, des requêtes, etc.).

Les deux analyses (lexicales et syntaxiques) utilisent de façon essentielle les automates, mais on retrouve aussi les automates dans de nombreux domaines de l’informatique. L’analyse lexicale s’explique dans le cadre restreint des automates finis et des expressions régulières (le terme français « autorisé » est expression rationnelle, mais je préfère adapter la terminologie anglaise). Les expressions régulières sont utilisées dans de nombreux outils Unix (éditeur de textes, commande grep etc.), et fournies en bibliothèque dans la plupart des langages de programmation.

Note L’étude détaillée des automates constitue un cours à part entière. Nous nous contentons ici de la présentation formelle minimale, avec comme but :

d’expliquer le fonctionnement des analyseurs de façon à pouvoir écrire soi-même des analyseurs lexicaux ou grammaticaux,
de se familiariser aussi avec les expressions régulières et les automates.

Le but du cours n’est pas d’écrire le moteur d’un analyseur, ni de répertorier toutes les techniques d’analyse, mais un peu de théorie ne nuit jamais (voir la section 4.6).

4.2 Les langages formels

On se donne un ensemble Σ appelé alphabet, dont les éléments sont appelés caractères. Un mot (sur Σ) est une séquence de caractères (de Σ). On note є le mot vide, uv la concaténation des mots u et v (la concaténation est associative avec є pour élément neutre). On note Σ ^∗ l’ensemble des mots sur Σ.

Un langage sur Σ est un sous-ensemble L de Σ^∗. On se donne quelques opérations sur les langages. Si U et V sont des langages sur Σ, on note U V l’ensemble des mots obtenus par la concaténation d’un mot de U et d’un mot de V; U ^∗ (resp. U ⁺), l’ensemble des mots obtenus par la concaténation d’un nombre arbitraire, éventuellement nul (resp. non nul) de mots de U.

4.2.1 Exemples

Σ₁ est l’alphabet français et L₁ l’ensemble des mots du dictionnaire français avec toutes leurs variations (pluriels, conjugaisons, etc.).
Σ₂ est L₁ et L₂ est l’ensemble des phrases grammaticalement correctes de la langue française. Un ensemble bien difficile à définir formellement. Ou bien, L₂′ est le sous-ensemble des palindromes de L₂.
Σ₃ est l’ensemble des caractères ASCII, et L₃ est composé de tous les mots-clés de Pseudo-Pascal, de l’ensemble des symboles, de l’ensemble des identificateurs et de l’ensemble des entiers décimaux.
Σ₄ est L₃ et L₄ est l’ensemble des programmes Pseudo-Pascal.
Σ₅ est {a, b} et L₅ est l’ensemble { a ⁿ b ⁿ ∣ n ∈ IN} (sous ensemble des expressions bien parenthésées).

4.3 Expressions régulières

La description de langages des mots (voir L₁ et L₃) qui servent à leur tour à définir des langages des phrases (voir L₂ et L₄) est relativement simple. On précise formellement cette simplicité en disant que ces langages des mots se décrivent à l’aide du formalisme relativement limité des expressions régulières.

On note a, b, etc. des lettres de Σ, M et N des expressions régulières, [[M]] le langage associé à M.

Une lettre de l’alphabet a désigne le langage {a}.
Epsilon : є désigne le langage {є}.
Concaténation : M N désigne le langage [[M]] [[N]].
Alternative : M ∣ N désigne le langage [[M]] ∪ [[N]].
Répétition : M^∗ désigne le langage [[M]] ^∗.

D’autres constructions sont utiles en pratique et exprimables à l’aide des précédentes :

[abc] pour (a ∣ b ∣ c) et [a₁−a₂] pour {c ∈ Σ, a₁ ≤ c ∧ c ≤ a₂}, en supposant que l’alphabet est ordonné.
M? pour M ∣ є, et M⁺ pour M M^∗.
[^abc] désigne le complémentaire de {a, b, c} dans Σ, vu comme des mots (et de même pour [^a₁−a₂]). L’interprétation est facile quand Σ est fini ce qui est toujours le cas.
On a aussi parfois point « . » (ou underscore _) pour Σ et ∗ pour Σ^∗. La première de ces construction est exprimable comme l’alternative de tous les caractères de l’alphabet, la seconde comme la répétition de la première.

Notons un point de vocabulaire. Lorsqu’un mot appartient à un langage défini par une expression régulière, on dit aussi l’expression (ici dénommée motif) filtre le mot.

Les langages réguliers sont ceux qui peuvent se définir à l’aide des expressions régulières. Dans nos exemples, L₁ est clairement régulier (alternative de tous les mots du dictionnaire, qui est fini) et nous allons voir comment exprimer L₃ avec des expressions régulières. C’est essentiellement l’absence de la récursion qui limite les langages réguliers, ainsi on peut montrer que le langage L₅ (les parenthèses) n’est pas régulier.

Le shell Unix utilise les expressions régulières pour spécifier les noms de fichiers. La commande suivante donne la liste de tous les sources Caml dans le répertoire courant :

#  ls *.ml{,[ily]}

Notez bien qu’ici l’alternative est exprimée avec la virgule « , », le mot vide par rien, et que les accolades sont un simple parenthésage. Dès lors, la commande précédente donne la liste des fichiers dont l’extension est .ml, .mli, .mll (sources du générateur d’analyseurs lexicaux ocamllex), et .mly (sources du générateur d’analyseurs syntaxiques ocamlyacc).

4.3.1 Utilisation pour l’analyse lexicale

Les lexèmes sont définis par l’alternative d’expressions régulières. Par exemple :

Les mots-clés : "let", "in". En général, les mots-clés ne peuvent pas être utilisés comme noms de variables. Ce parti pris évite pas mal d’ambiguïtés lors de l’analyse grammaticale ultérieure.
Les variables : ['A'-'Z' 'a'-'z'] ['A'-'Z' 'a'-'z' '0'-'9']*. Les noms des variables sont des suites de lettres et de chiffres commençant obligatoirement par une lettre.
Les entiers : ['0'-'9']+
Les symboles : '(', ')', '+', '*', '-', '/','='.
Un blanc : [' ' '\n' '\t']. Les caractères '\n' et '\t' sont respectivement le retour à la ligne et la tabulation.

On est passé ici en notation Caml, où un caractère est donné entre quotes (et une suite de caractères entre double quotes), si on veut le caractère quote « ' », il vaut mieux écrire '\''.

Une fois les lexèmes reconnus, ils sont représentés par un type somme dont nous noterons au passage qu’il n’est pas récursif :

type token = | LET | IN (* mots-clés *) | VAR of string (* variables *) | INT of int (* entiers *) | LPAR | RPAR | ADD | SUB | MUL | DIV | EQUAL (* symboles *)

On notera aussi que les blancs sont omis, c’est à dire qu’ils sont peut être des mots du langage mais sont oubliés en route. De fait les blancs servent surtout à séparer les lexèmes.

Il est bien connu que les automates finis (j’en dis un peu plus par la suite) savent reconnaître les langages réguliers, c’est à dire qu’étant donné un langage régulier L on peut construire un automate qui, lorsque l’on lui présente un mot sait répondre par oui ou par non à la question de l’appartenance du mot à L. Très rapidement, l’automate est un graphe dont les sommets sont des états et les arcs des transitions, l’automate est à un instant donné dans un état donné et la consommation d’une lettre du mot le fait changer d’état en suivant une transition. Lorsque le mot est entièrement consommé le mot est reconnu si l’état courant est un état particulier dit final. Par exemple, voici deux automates finis qui reconnaissent respectivement le mot-clé let et les entiers (suite non vide de chiffres). Dans ces dessins, les état initiaux sont grisés et les états finaux encerclés.

Dans le second automate, chaque transition en remplace dix, si on suit le formalisme strict des automates. Ensuite, pour reconnaître le mot clé let ou un entier, on peut regrouper les deux automates précédents :

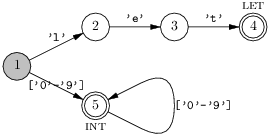
On a, ici dans un cas simple, construit l’automate qui reconnaît l’alternative de deux expressions régulières. Selon l’état final atteint (4 ou 5) on connaîtra le lexème reconnu.

Toutefois, ceci ne suffit pas tout à fait pour expliquer l’analyse lexicale, nous savons peut être reconnaître si un mot est dans L, mais nous devons, d’une part, reconnaître une suite de mots de L, et d’autre part, savoir de quels mots il s’agit. Intuitivement, un automate peut facilement reconnaître que le mot présenté est bien une suite de mots de L. En effet, le langage d’une suite de mots de L se définit à l’aide de l’opérateur de répétition ^∗. Mais on ne sait pas alors quels mots ont été reconnus, il vaut mieux reconnaître les mots un par un. Conceptuellement, il suffit d’arrêter l’automate dans un état final sans attendre la fin du mot, puis de recommencer sur la partie non consommée du mot présenté.

Mais il y a encore des cas douteux :

let pourrait être reconnu comme une variable.
lettre pourrait aussi être reconnu comme la séquence LET; VAR "tre" ou encore comme la séquence VAR "let"; VAR "tre".

Ces ambiguïtés se lèvent à l’aide de règles spécifiques. Lors de la reconnaissance d’un mot de L, on cherchera :

Le lexème le plus long possible.
Entre deux lexème de longueur maximale, l’ordre de présentation des sortes de mots lève l’ambiguïté, la première gagne.

Ainsi la phrase let lettre = 3 in 1 + fin devrait produire la suite de lexèmes :

LET; VAR "lettre"; EQUAL; INT 3; IN; INT 1; PLUS; VAR "fin"

En raison de la règle du lexème le plus long et à condition que, à taille égale, la reconnaissance des mots-clés prime celle des variables.

La règle de priorité numéro deux (sur l’ordre de présentation) se réalise simplement au moment de la fabrication de l’automate. Voici par exemple un automate qui reconnaît le mot-clé let ainsi que les identificateurs composés simplement de lettres minuscules, le mot-clé étant prioritaire.

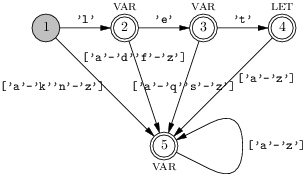
L’état final 4 pourrait bien correspondre à une variable ou à let, on choisit de le faire correspondre à la reconnaissance du mot-clé.

Sur cet exemple on peut aussi appréhender la réalisation de la règle du lexème le plus long. Tout en consommant les caractères de l’entrée, on peut se souvenir du dernier état final rencontré. Ensuite, lorsque l’automate est bloqué, ici par exemple si il y a un chiffre dans l’entrée, alors on peut revenir au dernier état final vu. Le blocage est facilement détecté en ajoutant un état dit bloqué à l’automate et en complétant les transitions issues de tous les états par des transitions vers l’état bloqué.

4.4 ocamllex

Nous ne savons pas précisément comment, à partir de la définition des lexèmes donnés comme expressions régulières, fabriquer l’automate qui les reconnaît. Nous admettons que cet automate existe. Bien mieux, il existe un programme ocamllex qui sait le construire pour nous.

L’outil ocamllex est lui même un compilateur, qui prend comme source les expressions régulières (dans un fichier nom.mll) et produit un programme Ocaml (dans un fichier nom.ml), programme qui réalise l’automate.

4.4.1 Un exemple simple

Figure 4.1: Analyseur lexical de la calculette

{ open Token exception Error } rule token = parse (* Les lexèmes stricto-sensu *) | '(' {LPAR} | ')' {RPAR} | '+' {ADD} | '-' {SUB} | '*' {MUL} | '/' {DIV} | '=' {EQUAL} | "let" {LET} | "in" {IN} | ['A'-'Z' 'a'-'z'] ['A'-'Z' 'a'-'z' '0'-'9']* {VAR (Lexing.lexeme lexbuf)} | ['0'-'9']+ {INT (int_of_string (Lexing.lexeme lexbuf))} (* Règles supplémentaires *) | eof {EOF} | [' ''\n''\t' ] {token lexbuf} | "" {raise Error}

Commençons par un exemple, celui d’un analyseur lexical pour calculette avec let. On écrit le source de la figure 4.1 dans un fichier lexer.mll, la commande :

# ocamllex lexer.mll

produit un nouveau fichier lexer.ml. L’exemple suffit déjà pour expliquer pas mal de choses sur la structure des fichiers source de ocamllex.

Le source commence par du code source Caml entre accolades, ocamllex copie ce code quel au début du fichier lexer.ml, de même on peut mettre du code Caml à la fin. Ici, le code donné en prélude commence par ouvrir le module Token, qui est supposé contenir la définition interne des lexèmes (autrement dit il existe un fichier token.mli qui contient la définition de type de la section 4.3.1). Cela permet d’écrire par exemple LPAR au lieu de Token.LPAR.
Ensuite, on trouve la définition de l’automate (ici dénommé token) sous forme d’une suite de règles introduites par les mots-clés (de ocamllex) rule et parse. Chaque règle est constituée d’une expression régulière (le motif) et d’une action, du code Caml à exécuter après reconnaissance. Les premières règles de la parenthèse ouvrante au mot-clé (de la calculette) in ne posent pas de problème, l’action est de rendre le lexème reconnu.
Ça se complique un peu pour les identificateurs, on voit apparaître la variable lexbuf et la fonction Lexing.lexeme dans l’action. La première est en fait l’argument implicite de l’analyseur, ie. la suite de caractère analysée, la seconde extrait la suite de caractères reconnue de lexbuf passé en argument. Le type des lexbuf est défini par le module Lexing de la bibliothèque standard, c’est une réalisation des suites de caractères qui répond aux besoins des analyseurs lexicaux. Dans ce cas l’entrée s’appelle aussi un flux. La règle des entiers s’explique de la même façon. En outre on convertit au passage la chaîne reconnue en entier.
Notons qu’à partir de la version 3.07 de Caml, on peut écrire.

| ['A'-'Z' 'a'-'z'] ['A'-'Z' 'a'-'z' '0'-'9']* as lxm {VAR lxm} | ['0'-'9']+ as lxm {INT (int_of_string lxm)}

C’est à dire qu’il est possible de lier la chaîne reconnue à une variable quelconque (ici lxm) à l’aide de la construction as.
Dans la règle suivante, le motif est le mot-clé (de ocamllex) eof. Cela indique la fin du flux d’entrée, l’automate rend alors un lexème spécifique qui aurait dû être ajouté à la définition des lexèmes de la section 4.3.1.
Ensuite, vient la règle de reconnaissance des blancs. On se contente de « manger » le blanc reconnu et de rappeler l’analyseur token, en lui passant explicitement l’entrée.
Enfin la dernière règle reconnaît le lexème vide. En raison de la règle du lexème le plus long, cette règle s’applique lorsqu’aucune des autres règles ne s’applique. Dès lors, elle identifie les erreurs.

Après la compilation de lexer.mll, le fichier lexer.ml contient donc la réalisation de l’automate token sous la forme d’une fonction de type Lexing.lexbuf -> Token.token. La « mission » de cette fonction est de reconnaître et renvoyer le lexème présent au début de son entrée et de consommer les caractères correspondants. La consommation des caractères n’est pas explicitée par le type, elle s’opère par effet de bord sur le flux passé en argument. À titre d’exemple, voici un petit bout de code Caml qui compte les lexèmes présents dans l’entrée standard.

let entrée = Lexing.from_channel stdin in (* Fabriquer le flux *) let count = ref 0 in while Lexer.token entrée <> Token.EOF do count := !count + 1 done ; Printf.printf "J'ai lu %d lexèmes\n" !count

4.4.2 Exemples plus compliqués

Mon propos n’est pas donner une description exhaustive de ocamllex. Ceux qui sont intéressés peuvent commencer par consulter le manuel. Je vais plutôt décrire quelques exemples et en profiter pour introduire d’autres traits de ocamllex.

Éliminer les commentaires

Commençons donc par considérer le cas des commentaires. Il est naturel de supprimer les commentaires dès l’analyse lexicale, ainsi les commentaires n’ont aucun impact sur toutes les phases suivantes du compilateur. Il y a trois sortes de commentaires.

Les commentaires s’étendent d’un mot particulier jusqu’à la fin de la ligne. C’est par exemple le cas en Java :

// Je suis un commentaire.

On élime facilement ce type de commentaire en ajoutant une règle à l’analyseur token.

| "//" [^'\n']* '\n'? {token lexbuf}

L’élimination s’opère comme pour les blancs en rappelant token récursivement. On doit bien remarquer que le motif qui filtre le texte du commentaire est [^'\n']* (une suite de caractères différents du retour à la ligne) et non pas _* (n’importe quel mot). En effet, avec le second motif, les commentaires s’étendraient du premier // au dernier retour à la ligne, en raison de la règle du lexème le plus long. On notera encore que le retour à la ligne est optionnel '\n'?, afin de considérer aussi un commentaire en fin d’entrée et sans retour à la ligne.
Les commentaires sont compris entre deux mots particuliers. mais ils ne peuvent pas être imbriqués. C’est le cas de la seconde sorte de commentaires de Java.

/* Je suis un commentaire, sur deux lignes. */

Pour éliminer ce type de commentaires on ne peut pas s’inspirer du cas précédent, car il n’y a pas de motif exprimant que l’entrée est différente d’un certain mot, comme il existe un motif exprimant que l’entrée est différente d’un certain caractère. Pour s’en sortir on a recours à un deuxième automate incomment, lancé à l’ouverture du commentaire et chargé de reconnaître la fin du commentaire.

rule token = parse ... | "/*" {incomment lexbuf} and incomment = parse | "*/" {token lexbuf} | _ {incomment lexbuf} | eof {raise Error}

L’automate incomment rappelle token dès qu’il voit la fin du commentaire, mange un caractère du commentaire et se rappelle, ou signale une erreur si l’entrée touche à sa fin avant la fermeture du commentaire.
À la reflexion, l’expression régulière suivante fonctionne aussi :

rule token = parse ... | "/*" ([^'*']|('*'+[^'*''/']))* '*'+ '/' {token lexbuf}

L’expression régulière ([^'*']|('*'+[^'*''/']))* décrit touts les mots qui ne contiennent pas "*/", sauf les suites non vides de '*', tandis que '*'+ '/' décrit les suites (possiblement vides) de '*' suivies de "*/". On peut trouver le premier motif en cherchant à expliciter le complément de "*/". Vous trouverez à la fin de la leçon une autre méthode pour trouver cette expression régulière.

Les commentaires sont compris entre deux mots particuliers et ils peuvent être imbriqués. Ce dernier type de commentaires permet de neutraliser du source dans un programme, y compris si le source commenté contient des commentaires. C’est le cas des commentaires de Caml.

(* Un commentaire (* avec un commentaire dedans *) *)

On ne peut plus utiliser un deuxième automate comme précédemment, car le niveau d’imbrication des commentaires est arbitraire. De fait, le langage formel défini informellement ci-dessus n’est pas régulier (c’est plus ou moins le langage des expression bien parenthésées) et donc il ne peut pas être reconnu par un automate fini. On pourrait en utilisant deux automates supplémentaires, reconnaître les commentaires imbriqués au plus une fois mais ce n’est pas très général. Pour s’en sortir on va ajouter de l’état aux automates, en se donnant un compteur depth du nombre de commentaires ouverts.

{ let depth = ref 0 } rule token = parse ... | "(*" {depth := 1 ; incomment lexbuf} and incomment = parse | "*)" {depth := !depth-1 ; if !depth <= 0 then (* où en sommes nous ? *) token lexbuf (* on ferme le premier "(*" *) else (* on ferme un autre "(*" *) incomment lexbuf} | "(*" {depth := !depth+1 ; incomment lexbuf} | _ {incomment lexbuf} | eof {raise Error}

Le compteur depth est logiquement incrémenté par chaque ouverture et décrémenté par chaque fermeture.

Il est possible de se passer du compteur global réalisé à l’aide de la référence depth et de le remplacer par un argument supplémentaire donné à la règle incomment.

rule token = parse ... | "(*" {incomment 1 lexbuf} and incomment depth = parse | "*)" {if depth <= 1 then (* où en sommes nous ? *) token lexbuf (* on ferme le premier "(*" *) else (* on ferme un autre "(*" *) incomment (depth-1) lexbuf} | "(*" {incomment (depth+1) lexbuf} | _ {incomment lexbuf} | eof {raise Error}

On notera enfin que les commentaires du source ci-dessus ne seraient pas correctement éliminés, en raison de la présence de la chaîne "(*" dans les commentaires. Il faudrait pour dépasser ce petit inconvénient, ignorer le contenu des chaînes dans les commentaires à l’aide d’un troisième automate.

Récupérer les chaînes

Considérons maintenant les chaînes (du langage analysé) définies comme tout ce qui se trouve entre deux caractères double quote « " ». On ajoute donc un lexème STRING of string au type des lexèmes et on cherche comment reconnaître les chaînes de l’entrée.

Si le double quote est interdit dans les chaînes, alors il n’y a pas de difficulté on s’en tire un peu comme dans le cas des variables.

| '"' [^'"']* '"' as lxm (* Noter: '"' est le caractère « " » *) {(* supprimer le premier et le dernier caractère de lxm *) STRING (String.sub lxm 1 (String.length lxm-2))}

On peut éviter l’appel aux fonctions du module String, car la construction as permet aussi de nommer des sous-chaînes de la chaîne reconnue par le motif. On écrira donc:

| '"' ([^'"']* as content) '"' {STRING content}

Mais le programmeur peut légitimement vouloir mettre un double quote dans une chaîne. Le concepteur prévoit alors un mécanisme de citation (quotation) : à l’intérieur d’une chaîne \" veut dire « " » et \\ veut dire « \ » (pour donner un moyen de mettre « \ » à la fin d’une chaîne). Je me félicite des guillemets français qui signifient ce caractère là. Comme il n’y a pas de notion de chaînes imbriquées dans les chaînes, on a le net sentiment que l’on va pouvoir s’en sortir à l’aide d’un automate supplémentaire instring, comme pour les commentaires /*… */. Il y a une petite différence, ici on doit renvoyer en résultat les caractères de la chaîne reconnue et non plus les ignorer. Pour éviter les recopies de chaîne en pagaille, ou pourrait employer des listes de caractères. Nous allons plutôt employer un tampon (buffer) tel que défini par le module Buffer de la bibliothèque standard (c’est en gros le même fonctionnement que la classe StringBuffer de Java).

Figure 4.2: Reconnaissance des chaînes

{ let sbuff = Buffer.create 16 (* fabriquer le buffer *) } rule token = parse ... | '"' {STRING (instring lexbuf)} and instring = parse (* Fin de la chaîne *) | '"' {let r = Buffer.contents sbuff in (* récupérer le contenu de sbuff *) Buffer.clear sbuff ; (* réinitialiser sbuff *) r} (* Caractères cités *) | '\\' ('"'|'\\' as c) (* c est le second caractère reconnu *) {Buffer.add_char sbuff c ; (* à mettre à la fin de sbuff *) instring lexbuf} | _ as c {Buffer.add_char sbuff c ; instring lexbuf} | eof {raise Error}

On notera d’abord, dans le code de la figure 4.2, l’utilisation de la la construction as pour récupérer un caractère de l’entrée. Ce qu’il faut remarquer c’est que, dans la construction motif as variable, variable est de type char quand motif est un motif caractères ou une alternative de motifs caractère. Jusqu’ici, motif pouvait filter des chaînes de longueur diverses et le type de variable était string.

On remarquera aussi que le type de l’automate instring est Lexing.lexbuf -> string. Enfin, on ne se laissera pas intimider par les mécanismes de citation de Caml : la notation '\\' désigne bien le caractère « \ ».

Abondance de mots-clés

Dans un langage programmation normal il y a souvent un nombre important de mots-clés. En principe cela ne pose pas de problème, il suffit de se donner une règle de reconnaissance par mot-clé et ocamllex construit l’automate. Mais en pratique, si il y beaucoup de mots-clés, l’automate sera gros voire énorme. On peut surmonter cet inconvénient en utilisant la clé anglaise de la programmation : la table de hachage. (La clé anglaise taiwanaise est un outil bon marché et polyvalent, mais moins efficace qu’une clé plate Facom de la bonne taille.) Les tables de hachage sont disponibles en Caml dans le module Hashtbl de la bibliothèque standard. Les tables de hachage définissent des associations de n’importe quoi à n’importe quoi, on les utilise ici pour définir une association des chaînes aux lexèmes. Une fois une suite de lettres reconnue, on vérifie si par hasard cette suite de lettres n’est pas un mot-clé. Si oui, on a reconnu le mot-clé, si non, on a reconnu un identificateur (voir la figure 4.3).

Figure 4.3: Reconnaissance a posteriori des mots-clés

{ let keywords = Hashtbl.create 17 (* création de la table de hachage *) (* initialisation de la table *) let _ = Hashtbl.add keywords "let" LET ; (* associer LET à "let" *) Hashtbl.add keywords "in" IN ; (* associer IN à "in" *) ... } rule token = parse ... | ['a'-'z']+ {let lxm = Lexing.lexeme lexbuf in try Hashtbl.find keywords lxm (* chercher lxm dans la table *) with Not_found -> (* lxm n'est pas un mot-clé *) Var lxm } (* c'est donc un identificateur *)

On remarquera l’utilisation plutôt simple des tables de hachage et le respect de la sémantique des mots-clés prioritaires sur les identificateurs.

Les erreurs

Pour le moment nos analyseurs se contentent signaler les erreurs, sans donner aucune information spécifique. On peut enrichir l’information donnée au programmeur en différenciant les erreurs, pour signaler un caractère illégal, une chaîne non-terminée etc. Mais l’information qui aidera sans doute le plus le programmeur est une position dans le fichier analysé. Or, dans une action, la fonction Lexing.lexeme_start (resp. Lexing.lexeme_end) fournit la position dans l’entrée du début (resp. de la fin) du dernier lexème reconnu. On peut alors transmettre cette position comme argument de l’exception Error en l’accompagnant d’un message d’erreur explicatif.

{ exception Error of int * string let error pos = raise (Error (pos,msg)) } rule token = parse ... | "" {error (Lexing.lexeme_start lexbuf) "Caractère illégal"} and incomment = parse ... | eof {error (Lexing.lexeme_start lexbuf) "commentaire non terminé"}

En fait, il faudrait travailler un petit peu plus pour par exemple transmettre la position du commentaire ouvert et non refermé.

Dans le cas où l’entrée est un fichier, la position comptée en caractères à partir du début du fichier est assez peu pratique, même si un éditeur tel que emacs sait automatiquement retrouver une telle position. Il est plus pratique de donner la position sous la forme d’un numéro de ligne et d’un compte de caractères à partir du début de la ligne. Considérons par exemple le fichier er.ml suivant :

let x = 1
let y = "coucou
let z = 1

La tentative de compilation ocamlc er.ml donne :

File "er.ml", line 2, characters 8-9:
String literal not terminated

Le compilateur retrouve assez facilement un numéro de ligne à partir d’une position (en réouvrant le fichier), et le confort d’utilisation gagné vaut ce petit effort.

Une autre possibilité est de tenter de corriger les erreurs (en les signalant tout de même !) et de reprendre l’analyse. On pourra par exemple simplement ignorer les caractères spéciaux. Mais c’est en fait difficile et souvent un peu vain, car l’analyseur aura du mal à deviner ce que le programmeur a en tête. Il ne saura pas, par example, où refermer une chaîne qui court jusqu’à la fin de l’entrée.

4.5 Bibliothèque des expressions régulières

Un outil tel que ocamllex facilite l’écriture des analyseurs lexicaux, mais il n’est pas très pratique pour programmer à l’aide des expressions régulières, comme on le fait par exemple beaucoup en Perl. En effet, on doit mettre l’analyseur dans son propre fichier .mll ce qui est un peu lourd. Par ailleurs, les générateurs d’analyseurs lexicaux visent plutôt un public de concepteurs de compilateurs et leurs concepteurs ne proposent pas toujours quelques traits courants et pratiques qui séduisent le plus vaste public des programmeurs. Des bibliothèques « d’expressions régulières » répondent à ce besoin de plus grande flexibilité et d’expressivité étendue.

En Caml, on dispose de la bibliothèque Str. Elle ne sera pas décrite ici, ceux qui sont intéressés peuvent consulter le manuel. Il y a deux points notables :

Le parti-pris syntaxique est à l’opposé de ocamllex : au lieu de citer les caractères de l’alphabet on cite les constructions des expressions régulières. En ocamllex on écrivait ('a'|'b'), en Str on écrira $a\|b$. Enfin, ce n’est pas tout à fait exact, les caractères $^.*+?[] sont spéciaux et doivent parfois être cités avec « \ » pour se signifier eux mêmes.
Un trait supplémentaire intéressant est que, en cas de réussite du filtrage, le parenthésage permet d’extraire des sous-chaînes de la chaîne filtrée.

Nous nous contenterons donc d’un exemple simple. Nous cherchons à reconnaître des adresses de courrier électroniques de la forme Prénom.Nom@polytechnique.fr, afin d’en extraire le nom. En outre, nous acceptons les variations de casse dans le nom de domaine polytechnique.fr. Le code est donné par la figure 4.4.

Figure 4.4: Exemple d’utilisation de la bibliothèque Str

open Str open Printf (* - ^ initial -> début de ligne - [^.] -> tout sauf le point - \. -> un point - $... $ -> groupage, groupes numérotés de gauche à droite - .* -> n'importe quelle chaîne - $ -> fin de ligne *) let auto = regexp "^[^.]+\.$[^@.]+$@$.*$$" (* compilation de l'automate *) let extrait s = if string_match auto s 0 && (* filtrage *) String.lowercase (matched_group 2 s) = (* extraction 2ème groupe *) "polytechnique.fr" then printf "Le nom est %s\n" (matched_group 1 s) (* extraction 1er groupe *) else printf "Ce n'est pas une adresse de l'X\n"

La bibliothèque Str ne fait pas partie de la bibliothèque standard. Par conséquent, l’argument str.cma doit être donné explicitement lors de l’édiction de liens:

# ocamlc options str.cma files…

4.6 Un peu de théorie

Cette section culturelle explique les principes des générateurs d’analyseurs lexicaux tels que ocamllex. Le principe général est celui d’une véritable compilation des expressions régulières aux automates.

4.6.1 Automates finis déterministes (DFA)

Un automate fini déterministe M est un quintuplet (Σ, Q, δ, q₀, F) où

Σ est un alphabet;
Q est un ensemble fini d’états;
δ : Q × Σ → Q est la fonction (partielle) de transition;
q₀ est l’état initial;
F est un ensemble d’états finaux.

On peut étendre δ sur Q × Σ ^∗→ Q par

⎧
⎨
⎩

δ (q, є) = q

δ (q, aw) = δ (δ (q, a), w)

Le langage L(M) reconnu par l’automate M est l’ensemble { w ∣ δ (q₀, w) ∈ F } des mots permettant d’atteindre un état final à partir de l’état initial.

Exemple Soit un automate :

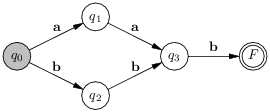
L’automate reconnaît le langage {aab, bbb}, La formalisation comme un quintuplet est laissée en exercice.

4.6.2 Automates finis non-déterministes (NFA)

La définition est la même que celle de automates déterministes, compte tenu des deux détails suivants :

Les transitions sont définies par une relation et non plus par une fonction, c’est à dire que plusieurs transitions issues d’un état donné peuvent porter la même étiquette.
Il existe des transitions « spontanées » qui portent une étiquette spéciale, classiquement є.

On peut exprimer ces modifications en définissant les transitions entre états comme une relation δ (fonction dans les booléens) sur Q × (Σ ∪ {є}) × Q. Une telle relation peut aussi très bien se noter comme une liste de triplets q ↦^a q′.

On étend δ sur Q × Σ ^∗× Q par

⎧
⎪
⎨
⎪
⎩

	δ(q,є, q)

δ(q,є, q″) ∧ δ(q″, w, q′)	⇒	δ(q, w, q′)
δ(q, a, q″) ∧ δ(q″, w, q′)	⇒	δ(q, aw, q′)

(Il y a un peu d’abus, la relation définie est le point fixe des implications et il y a quelques quantificateurs implicites.)

Le langage L(M) reconnu par un automate non déterministe est {w ∣ ∃ q_f ∈ F, δ (q₀, w, q_f)} . Notons, et c’est assez intéressant, que les transitions définissent aussi une fonction de Q × Σ ^∗ vers 2^Q (ensembles d’états) : à un état q et un mot w, on associe l’ensemble Q′ des états q′ tels que la relation δ(q, w, q′) tient.

Exemple Soit un automate :

L’automate reconnaît le langage des mots d’au moins une lettre formés avec a et b. On note que le mot ab peut être reconnu de deux façons différentes (à q₀ et ab, on associe {q₀, F₁, F₂}). On peut intuitivement voir la reconnaissance d’un mot par un tel automate comme le calcul d’un ensemble d’états effectués ainsi.

Initialement, l’ensemble des états est l’état initial plus tous les états accessibles par une suite de transitions spontanées.
Pour consommer un caractère a, l’automate suit toutes les transitions étiquetées par a et issues de son ensemble d’états courant. Ensuite, il complète le nouvel ensemble d’états courants comme initialement.

Ainsi la consommation du mot ab peut se décrire par les trois dessins suivants (cette fois ci, c’est l’ensemble des états courants qui est grisé).

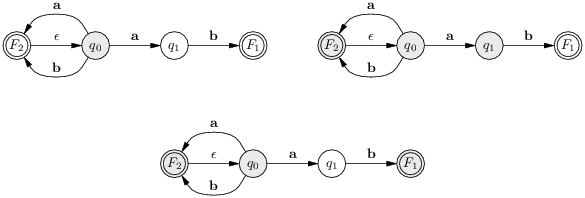
4.6.3 Compilation des expressions régulières

Nous sommes maintenant équipés pour décrire la fabrication d’un automate fini déterministe reconnaissant un langage régulier donné. Il s’agit d’une véritable compilation qui comprend trois phases successives¹.

Des expressions régulières aux NFA

L’intérêt des automates non-détermistes est qu’il est facile d’associer un automate (Q, δ, s, F) reconnaissant un langage L à une expression régulière M définissant le langage L.

[[a]] = ({s, f}, {s ↦^a f}, s, {f})
[[є]]= ({s, f}, {s ↦^єf}, s, {f})
[[M ∣ M′]] = (Q ∪ Q′ ∪ {s″}, δ ∪ δ′ ∪ { s″ ↦^єs, s″ ↦^єs′ }, s″, F ∪ F′)
[[M M′]] = (Q ∪ Q′, δ ∪ δ′ ∪ {f ↦^єs′, f ∈ F}, s, F′)
[[M^∗]] = (Q, δ ∪ {f ↦^єs, f ∈ F}, s, {s})

Ce n’est pas la seule construction possible. Par exemple, on peut exprimer graphiquement une construction légèrement différente (la modification ne porte que sur l’alternative). La nouvelle construction produit des automates à un seul état initial et un seul état final. Ces automates sont représentés par des boîtes portant le nom du motif représenté, leur état initial est à gauche et leur état final à droite.

Le motif est a, є ou un motif [ab] (en optimisant un peu par rapport à l’expansion en a ∣ b).
Le motif est M N ou M ∣ N.
Le motif est M^∗, on notera qu’aucun état n’est ajouté.

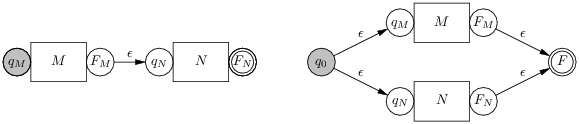
La première construction de l’alternative à l’avantage de laisser intacts les états finaux, de sorte qu’ils dénonceront plus tard la branche choisie. Ainsi, en suivant la première construction de l’alternative et en optimasant le motif [ab], l’expression régulière ([ab]+ ∣ ab) se compile en l’automate suivant :

Des NFA aux DFA

On peut très bien exécuter directement un automate non-déterministe, en considérant un ensemble d’états courants. Mais la manipulation des ensembles coûte toujours un peu cher, et dans un contexte de compilation, il vaut mieux transformer les NFA en des DFA équivalents (ie. qui reconnaissent le même langage). Cela revient à payer le prix de la réalisation des ensembles une seule fois, et est particulièrement rentable lorsque l’analyseur a vocation a être exécuté de nombreuses fois.

L’idée est inspirée de l’exécution des automates non-deterministes, il suffit de considérer tous les ensembles d’états possibles durant toutes les exécutions possibles. Soit, à partir d’un NFA A_n = (Q, δ, q₀, F) on souhaite trouver un DFA équivalent A_d = (R, γ, Q₀, G). On choisira les états de A_d parmi l’ensemble des parties de Q, on notera donc les états de A_d, Q₀, Q₁, etc. On définit deux fonctions sur 2^Q.

la fermeture F, comme le point fixe de S = S ∪ { q ∣ ∃ q′ ∈ S, δ(q′, є, q)} (autrement dit, on suit toutes les transitions spontanées possibles issues des états de S).
la consommation d’un caractère a, noté C_a comme C_a(S) = {q ∣ ∃ q′ ∈ S, δ(q′, a, q)}.

L’algorithme de traduction consiste à tout simplement calculer l’ensemble des ensembles d’états atteignables (les Q_i) à partir de l’état initial de A_n, en se rappelant au passage des transitions entre les Q_i. Plus formellement, on calcule le point fixe

R = F({q₀}) ⋃ {Q_i ∣ ∃ Q_j ∈ R ∧ ∃ a ∈ Σ , Q_i = F(C_a(Q_j))} ⋃ R

Avec en outre, γ(Q_j, a) défini comme Q_i = F(C_a(Q_j)), et G composé des états de R qui contiennent au moins un état final de F.

Ça à l’air un peu compliqué, mais un exemple expliquera mieux ce qui se passe. Considérons toujours le même automate, celui qui résulte de la compilation de ([ab]+ ∣ ab), en se plaçant dans l’alphabet Σ = {a, b}. Dans un premier temps, nous disposons de l’état initial Q₀ = F({q₀}) = {q₀, q₁, q₄} les états et les transitions sont ensuite calculées ainsi :

Q₁ = F(C_a(Q₀)) = {q₂, q₃, q₅, q₆, F₂} avec donc Q₀ ↦^a Q₁.
Q₂ = F(C_b(Q₀)) = {q₅, q₆, F₂}, avec donc Q₀ ↦^b Q₂.
Q₃ = F(C_a(Q₁)) = {q₆, F₂}, avec donc Q₁ ↦^a Q₃. On remarque aussi que l’on a Q₃ = F(C_a(Q₃)) et Q₃ = F(C_b(Q₃)), on peut donc ajouter deux transitions Q₃ ↦^a Q₃ et Q₃ ↦^b Q₃ et aucun nouvel état.
Q₄ = F(C_b(Q₁)) = {q₆, F₁, F₂}, avec donc Q₁ ↦^b Q₄.
On a Q₃ = F(C_a(Q₂)) et Q₃ = F(C_b(Q₂)), soit encore deux nouvelles transitions vers Q₃, Q₂ ↦^a Q₃ et Q₂ ↦^b Q₃.
Et il en va de même pour Q₄ : on a Q₃ = F(C_a(Q₄)) et Q₃ = F(C_b(Q₄)).

Le calcul est maintenant terminé, car le cas de la consommation de a et b a été examiné à partir de tous les états possibles de A_d et on obtient donc l’automate de la figure 4.5.

Figure 4.5: Automate de ([ab]+|ab)

Il est maintenant intéressant d’examiner l’état Q₄ qui contient les deux états finaux du NFA F₁ et F₂. Cet état n’est atteint que si l’entrée est ab. Or, F₁ traduit le filtrage de cette entrée par le motif ab, tandis que F₂ traduit le filtrage par [ab]+. Ce n’est pas bien grave si on ne s’intéresse qu’à la définition du langage reconnu. En revanche, si l’automate est censé reconnaître un mot-clé (ab) et des variables ([ab]+), il faut faire un choix. Le choix est arbitraire et repose sur l’ordre de présentation des motifs. On suppose pour la suite que ab prime sur [ab]+ et on décore les états finaux par le motif choisi. On obtient l’automate de la figure 4.6.

Figure 4.6: Automate de ([ab]+|ab), états finaux distingués

Minimisation des DFA

L’automate déterministe donné comme compilation de ([ab]+|ab) n’est pas optimal : il existe un automate plus petit qui reconnaît le même langage que lui. De fait, selon que l’on souhaite distinguer les motifs reconnus ou pas et en revenant à l’expression régulière on trouve facilement deux automates équivalents (voir la figure 4.7).

Figure 4.7: Automates optimaux

Évidemment on peut maintenant se demander comment produire un automate optimal à partir d’un automate donné. Je vais juste donner l’idée. Deux états Q_i et Q_j de l’automate donné sont équivalents, noté Q_i ≅ Q_j, quand les suffixes du langage L reconnus à partir de ces états sont exactement les mêmes. On peut fusionner les états équivalents, le langage reconnu ne changera pas. Tous les états finaux de l’automate de la figure 4.5 sont équivalents. En effet toutes les reconnaissances amorcées à partir de ces états définissent le langage [ab]*, on peut alors à fortiori fusionner Q₁, Q₂, Q₃ et Q₄ en S₁. Notons que si l’on distingue les états finaux (figure 4.6), alors on ne peut fusionner que Q₂ et Q₃.

Le principe d’un algorithme de minimisation est de remplacer les états par les classes d’équivalence de ≅. Un algorithme possible fonctionne par raffinements successifs d’une partition initiale des états en états finaux et non finaux (si les états finaux sont distingués, il y a un élément de la partition initiale par sorte d’état final), jusqu’à obtenir une partition stable sous la relation δ(_,a) pour tous les caractères a. Plus précisément la relation recherchée est :

∀ R ∈ P, ∀ Q,Q′ ∈ R × R, ∀ a ∈ Σ, ∃! R′, δ (Q,a) ∈ R′ ∧ δ (Q′,a) ∈ R′

Il y a de nombreuses variations de cette idée, les variations concernent surtout l’arrangement des itérations et les structures de données. L’algorithme le plus efficace utilise la relation inverse δ⁻¹.

4.6.4 Réalisation des automates

On peut réaliser les automates directement par du code. En Caml on aura recours à une fonction par état, chaque fonction filtrant le caractère courant. Ainsi, l’automate optimal de gauche de la figure 4.7, donnerait lieu à ce genre de code :

Mais le code risque d’être assez abondant. On a plutôt tendance à définir l’automate par la table de ses transitions, c’est à dire comme une matrice d’entiers, les lignes étant les états et les colonnes les caractères. Ainsi sur l’alphabet {a, b, c} on a la matrice de transitions :

⎛
⎜
⎜
⎜
⎝

1	3	−1
3	2	−1
3	3	−1
3	3	−1

⎞
⎟
⎟
⎟
⎠

⎛
⎜
⎜
⎜
⎝

−

"[ab]+"

"ab"

"[ab]+"

⎞
⎟
⎟
⎟
⎠

Une entrée −1 indique une erreur et le vecteur de droite désigne les états finaux. On peut alors interpréter la table pour réaliser l’automate spécifié. Le calcul d’une transition prend un coût constant, car il consiste à accéder dans un tableau. A priori nous n’avons pas gagné beaucoup de place (car il y a normalement de l’ordre de 256 caractères possibles), mais les matrices de transition sont souvent creuses (chaque ligne possède beaucoup de valeurs identiques). On peut alors représenter la matrice de transition de façon compacte en pratique, tout en gardant un coût constant pour la réalisation d’une transition.

4.6.5 Exemple d’exercice sur les automates

Rappelons que le problème est de trouver une expression régulière qui décrit les commentaires de C : il s’étendent d’un mot "/*" au premier mot "*/" qui suit. Or, on peut assez facilement trouver l’automate déterministe qui, laché dans un commentaire, sait en trouver la fin :

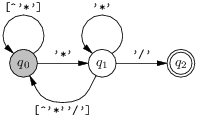
Ensuite on cherche à trouver une expression régulière décrivant le langage de cet automate. On va donc inverser la construction présentée précédemment dans un cas particulier. On duplique d’abord l’état q₁ en répartissant astucieusement ses transitions. On a alors l’automate non-déterministe équivalent suivant :

Soit encore, en dupliquant q₀ cette fois :

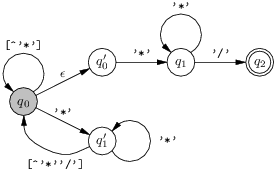
Nous retrouvons maintenant la composition en séquence des deux automates suivants :

Le langage de l’automate de gauche est ([^'*']|('*''*'*[^'*''/'])* (répétition des deux sortes de chemins possibles de q₀ à lui même) tandis que le langage de l’automate de droite est '*'+ '/' (facile). Bon, la dérivation de l’expression régulière à partir de l’automate déterministe manque de généralité, mais elle est correcte. L’idée étant de vérifier à chaque étape que les chemins de l’état initial à l’état final ne changent pas.

1: ocamllex procède en fait en une seule passe, qui combine les deux premières phases de notre description.