


Chapitre 5 Analyse grammaticale
Comme déjà dit, l’analyse grammaticale fabrique
l’arbre de syntaxe abstraite à partir des lexèmes produits par
l’analyse lexicale.
L’arbre de syntaxe abstraite est important,
car il est le support de la sémantique du langage.
Il importe donc, pour comprendre ce que fait exactement un programme,
de bien comprendre d’abord comment son source s’explique en
terme de syntaxe abstraite.
Il n’est pas surprenant que cette compréhension découle directement
d’une connaissance un peu fine du processus de l’analyse grammaticale.
Le mieux est je crois, pour être précis, de donner un tour théorique
au discours.
5.1 Grammaires
Les grammaires algébriques définissent une classe bien particulière de
langages formels (voir le chapitre précédent, section 4.2) :
les langages algébriques (context-free).
Dans ce cadre, les lettres de l’alphabet Σ s’appellent les
(symboles) terminaux et sont notés par des minuscules a, b,
c etc. ou
parfois id, int, +, lorsque qu’ils sont connus.
On se donne un ensemble de nouveaux symboles V, dits
non-terminaux que nous noterons par des majuscules, A B, C etc.
Les symboles de la grammaire sont à la fois les terminaux (pris
dans Σ) et les
non-terminaux (pris dans V), quand nous parlons d’eux
nous les noterons à l’aide de lettres grecques majuscules
Δ, Γ etc.
Dans le même ordre d’idée, nous noterons les mots formés de symboles
terminaux et non-terminaux. par des lettres grecques minuscules,
α, β, γ, etc.
Toutefois, La lettre grecque є désigne toujours le mot vide.
Un non-terminal particulier est dit symbole de départ.
Une grammaire algébrique (context-free) est une liste de
productions de la forme A → α.
On regroupe parfois plusieurs productions de même membre gauche
A → α1,
A → α2, … , A → αn en écrivant
A → α1 ∣ α2 ∣ … ∣ αn.
Le langage L(G) engendré par une grammaire G est l’ensemble des
mots produit en partant du symbole de départ S (souvent sous-entendu)
et en appliquant la démarche suivante aux mots α :
-
Si α n’est formé que de terminaux alors α est un
mot w de L(G).
- Sinon, α peut se décomper en βAγ, où A est
un non-terminal.
- Alors, on considère une production A → δ,
on remplace A dans α par δ, noté
α ⇒ βδγ et on recommence en 1.
L’opération décrite s’appelle une dérivation de w et se note
S ⇒*w (w est un mot de terminaux).
On utilise la même notation pour les étapes intermédiaires
α ⇒*β, où α et β sont des mots de
symboles quelconques de la grammaire.
la figure 5.1 donne une grammaire G des expressions arithmétiques.
| Figure 5.1: Une grammaire pour les expressions
arithmétiques |
Et voici trois dérivations de la même expression arithmétique
1 + 2 * 3
en admettant que 1, 2 et 3 sont des entiers
int1, int2 et int3 :
| E ⇒
E + E ⇒
E + E * E ⇒
1 + E * E ⇒
1 + 2 * E ⇒
1 + 2 * 3 |
|
|
E ⇒
E * E ⇒
E + E * E ⇒
1 + E * E ⇒
1 + 2 * E ⇒
1 + 2 * 3 |
|
|
E ⇒
E + E ⇒
1 + E ⇒
1 + E * E ⇒
1 + 2 * E ⇒
1 + 2 * 3
|
|
(Le non-terminal substitué par le membre droit d’une production à
chaque étape est souligné et le remplacement apparaît comme ça.)
La question de l’analyse syntaxique consiste d’abord à décider
si un mot de non-terminaux quelconque appartient à L(G) ou pas,
autrement dit de trouver une dérivation du mot.
En pratique l’analyse syntaxique revient aussi à donner un
« sens » au mot.
Ainsi si nous considérons le mot 1 + 2 * 3, nous savons maintenant de
façon trois fois certaine qu’il s’agit bien
d’un mot de L(G).
Le sens à lui donner serait normalement un arbre de syntaxe abstraite
mais ici nous pouvons aussi l’exprimer comme l’entier résultat du
calcul proposé.
L’idée est de parcourir les dérivations en replaçant les
productions de la forme E → E op E par l’opération
correspondante et les autres productions par rien.
À ce compte, seules deux productions importent et nous obtenons les calculs
suivants (à lire de la droite vers la gauche) :
Un analyseur syntaxique va partir du mot
w = 1 + 2 * 3
et chercher à produire une dérivation de E qui engendre ce mot.
C’est cette dérivation qui est le support de ce
qu’un compilateur situé en aval de l’anlyseur comprendra.
On constate ici que :
-
la première et la troisième dérivation produisent le même sens,
- la première et la deuxième dérivation produisent un sens distinct
La première remarque nous conduit à penser que les dérivations sont
trop précises, seul importe ici le choix de la première
production utilisée.
On peut l’exprimer mieux en considérant des arbres de dérivation.
Un tel arbre se construit à partir d’une dérivation quelconque
en appliquant les productions non plus sur des mots des symboles de la
grammaire mais sur une stucture d’arbre ad-hoc.
Ainsi, la première dérivation nous donne les arbres successifs :
(Le mot de chaque étape se retrouve en lisant les feuilles de l’arbre de la
gauche vers la droite.)
Deux derivations qui ont le même sens produisent au final le même
arbre. Ainsi, toutes les dérivations possibles de
w = 1 + 2 * 3 s’expriment en deux
arbres :
On observe maintenant que l’arbre de syntaxe abstraite traditionnel se
déduit de l’arbre de dérivation en enlevant touts les non-terminaux
(et les parenthèses, redondantes dans une structure arborescente).
Ici on obtient les deux arbres de syntaxe abstraite.
On peut alors aussi dire (et c’est exactement la même chose) que
1+2*3 pourait se comprendre comme 1+(2*3) ou (1+2)*3.
Lorsque l’on raisonne sur les analyses il n’est pas commode de faire
des dessins d’arbre.
On désigne donc une classe de dérivations équivalentes (ie. qui ont
le même arbre de dérivation au final) par une dérivation particulière.
On a ainsi les dérivations gauches (resp. droites) qui
consistent à substituer toujours le non-terminal le plus à gauche
(resp. à droite) dans la chaîne de symboles en cours de dérivation.
Il existe une unique dérivation gauche (une unique dérivation droite)
dans une classe de dérivations équivalentes.
Intuitivement, cela veut dire que l’ordre dans lequel on calcule les
arguments des opérations n’a pas d’importance.
Ainsi nos deuxième et troisième dérivations sont gauches.
et puisque nous pouvous exhiber deux dérivations gauches (ou deux
arbres de dérivation) du mot w = 1 + 2 *
3, notre grammaire ne donne pas un sens bien clair aux
expressions arithmétiques. On dit qu’elle est ambigüe.
Afin de donner un sens clair à la syntaxe concrète on souhaite
disposer d’une grammaire G′,
équivalente à G (ie. qui définit le même langage) et non-ambigüe.
Soit une grammaire G′ pour laquelle il existe une unique dérivation
gauche (ou droite) de tout les mots de L(G′) = L(G).
Or, dans le cas des expressions arithmetiques, on sait comment
procéder depuis l’école primaire. Il suffit d’effectuer les
multiplications et les
divisions avant les additions et les soustractions.
En outre, il faut aussi effectuer les
soustractions et les divisions de la gauche vers la droite
(1−2−3 se calcule comme (1−2)−3 et non pas comme 1−(2−3)).
Remarquons que, si seule la valeur entière d’une expression nous
intéressait, nous aurions pu oublier ce dernier point dans le cas de
l’addition et de la multiplication qui sont associatives.
Mais ce n’est de toute façon pas sain, car pour donner une sémantique
précise aux programmes, il convient de définir
précisément la syntaxe abstraite en fonction de la syntaxe concrète.
À partir de ces intuitions nous pouvons produire
la grammaire G′ de la figure 5.2.
Cette grammaire est certainement équivalente à G et non-ambigüe,
nous l’utilisons depuis
l’enfance pour nous parler entre nous de tous les calculs élémentaires
possibles, et nous nous comprenons.
| Figure 5.2: Une grammaire non-ambigüe pour les
expressions arithmétiques |
5.2 Analyse descendante (top-down parsing)
Une fois bien défini le langage à analyser, c’est à dire une fois posée
une grammaire G.
Nous voulons d’abord vérifer
qu’un mot w de Σ ∗ (une suite de lexèmes) appartient
bien à L(G).
Un première intuition est la suivante :
G′ n’est pas ambigüe (et L(G) = L(G′)), il existe donc
un unique arbre de dérivation de w.
Dans le cas de notre exemple, le voici :
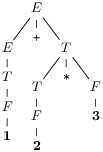
Nous aimerions alors faire correspondre chaque non-terminal de cet arbre
à un appel de fonction, et chaque terminal à
la consommation d’un lexème dans un flux.
Observons d’abord que cela revient à construire l’arbre de dérivation
de la racine vers les feuilles et que le flux impose que l’arbre se
construise de gauche à droite (et donc on reconstitue une dérivation
gauche, dans le bon ordre).
Dans cet exemple, nous aimerions appeler E d’abord, qui
appelle E, puis consomme +, puis appelle T.
Le premier appel recursif de E devrait appeler T, qui appellerait
F qui consommerait enfin le lexème 1. Ensuite après les
retours de F puis de T, + serait en tête du flux, prêt à
être consommé par l’appel initial de E.
Si nous cherchons maintemant à écrire la fonction expr
correspondant à E,
nous sommes immédiatement confrontés à un premier problème grave :
expr doit commencer par appeler expr
sans rien consommer dans le flux. Dès lors,
tout appel à expr bouclera d’entrée de jeu.
Sur la gramaire G′ le problème est révélé par
la production E → E + T où E apparait en tête du membre
droit. Une telle production est dite récursive à gauche.
Tant qu’il ne s’agit que de reconnaître L(G) nous pouvons très bien
utiliser la grammaire G″ de la figure 5.3 qui est
équivalente à G et n’est pas récursive à gauche.
| Figure 5.3: Une autre grammaire non-ambigüe pour les
expressions arithmétiques |
Nous pouvons maintenant examiner l’écriture de l’analyseur d’un peu
plus près.
Nous nous donnons le cadre suivant :
-
Nos lexèmes sont ceux de la section 4.3.1.
- Nous pouvous appeler et définir des fonctions récursives.
Notre analyseur est une fonction qui renvoie
() si le flux
contient un mot de L(G), et qui sinon, lève l’exception Error.
- Nous pouvons regarder quel est le lexème en attente (fonction
look de type flux -> token)
- Nous pouvous manger le lexème en attente (function
eat de
type flux -> unit)
- Nous pouvons vérifier que le lexème en attente
et le manger (fonction
is de type
flux -> token -> unit). C’est une commodité qui s’écrit à l’aide des deux fonctions
précédentes :
| let is flux tok =
if look flux = tok then eat flux
else raise Error |
Pour vérifier que l’entrée est bien un E (ie. qu’il existe une
dérivation de E vers w) nous devons de toute façon commencer par
appeler term (qui correspond à T).
Ensuite, au retour de term si tout s’est bien
passé, nous allons regarder en tête de l’entrée.
Il y a alors deux cas :
-
Si nous voyons + ou -, nous le consommons puis
appelons expr.
- Sinon, seule la production T → F peut s’appliquer,
T est déjà reconnu. La fonction expr retourne
immédiatement.
Bref, nous transformons la grammaire G″ en le programme de la
figure 5.4.
| Figure 5.4: Un analyseur écrit à la main |
| let rec expr flux =
term flux ;
begin match look flux with
| (ADD|SUB) -> eat flux ; expr flux
| _ -> ()
end
and term flux =
factor flux ;
begin match look flux with
| (MUL|DIV) -> eat flux ; term flux
| _ -> ()
end
and factor flux = match look flux with
| INT _ -> eat flux
| LPAR -> eat flux ; expr flux ; is RPAR flux
| _ -> raise Error |
| Figure 5.5: Raffinement du programme 5.4 pour construire
l’arbre de syntaxe abstraite |
| type ast = Int of int | Binop of binop * ast * ast
and binop = Add | Sub | Mul | Div
let rec expr flux =
let t1 = term flux in
match look flux with
| ADD -> eat flux ; Binop (Add, t1, expr flux)
| SUB -> eat flux ; Binop (Sub, t1, expr flux)
| _ -> t1
and term flux =
let t1 = factor flux in
match look flux with
| MUL -> eat flux ; Binop (Mul, t1, term flux)
| DIV -> eat flux ; Binop (Div, t1, term flux)
| _ -> t1
and factor flux = match look flux with
| INT i -> eat flux ; Int i
| LPAR ->
eat flux ;
let t = expr flux in
begin match look flux with
| RPAR -> t
| _ -> raise Error
end
| _ -> raise Error |
Si nous voulons aussi vérifier que toute l’entrée est bien
un E, alors nous utilisons le lexème eof.
On complète la grammaire par une production
S → E eof et le programme par une fonction :
| let start flux = expr flux ; is EOF flux |
Mais un compilateur ne saurait se contenter de vérifier que son entrée
est correcte, il cherche à donner un sens à cette entrée en terme de syntaxe
abstraite.
C’est assez facile (figure 5.5), au lieu de ne rien faire en cas
de succès, on construit l’arbre (de syntaxe abstraite).
On notera que l’arbre de syntaxe abstraite produit ne correspond pas
aux habitudes 1−2−3 est interprété comme 1−(2−3).
On peut tout de même arriver à produire l’arbre de syntaxe abstraite
qui obéit aux
conventions usuelles sans boulverser la structure de l’analyseur.
Ce programme est laissé en exercice complémentaire
(solution à la fin).
En ce qui concerne la réalistion de l’analyse syntaxique, il y a une
différence notable entre le schéma fonctionnel de la chaîne de
compilation et l’organisation des rapports entre les analyseurs lexical
et grammatical.
La chaîne de compilation fait
apparaître deux phases successives : d’abord l’analyse lexicale qui
produit une suite de lexèmes, puis l’analyse grammaticale consomme
cette suite.
Mais en pratique les appels à l’analyseur lexical sont opérés par
l’analyseur grammatical en fonction de ses besoins.
Ils sont mieux décrits par le schéma de la figure 5.6.
| Figure 5.6: Rapports entre les analyseurs selon des flux. |
L’analyseur lexical consomme les caractères de l’entrée un par un à la
demande, c’est la boite flux qui offre cette interface, et de même
l’analyseur lexical montre un flux de lexèmes à l’analyseur
grammatical.
Le schéma simplifie un peu les choses, mais il est conceptuellement
facile d’offrir nos fonctions look et eat à partir
de next_token et d’un tampon pouvant contenir un lexème.
Le principal impact ce cette technique en deux flux est que la
mémoire nécessaire pour stoker les lexèmes utiles à un instant donné
est constante.
Si on produisant d’abord disons une liste de tous les lexèmes,
l’analyse demanderait nécessairement une taille mémoire
proportionnelle à la longeur de l’entrée.
5.3 Analyse LL
Sans tenir du miracle, la démarche de la section précédente semble
quand même un peu difficile à appliquer mécaniquement.
J’illustre maintenant la production systématique d’un analyseur
similaire à partir de la grammaire 5.1, augmentée d’une
production S → E eof.
Soit en fait une compilation des grammaires vers les analyseurs.
La cible de ce genre de compilation est traditionnellement un
automate. Il ne surprendra personne que cet automate est muni d’une
pile.
Toutefois, je préfère choisir comme cible une classe restreinte de programmes
Caml, que je pense du même ordre de puisssance que
l’automate traditionnel.
-
Le programme est une définition de fonctions récursives qui
prennnent un flux en argument.
Il y a une fonction parseA par non-terminal A.
- Chaque fonction doit appeler
look initialement.
et filtrer le résultat de cet appel (par un filtrage match
look flux with).
- Les actions du filtrage de parseA sont obligatoirement
des séquences
d’appels aux fonctions définies en 1. et à is.
Elles s’ecrivent mécaniquement à partir du membre droit α d’une production
A → α en remplaçant les non-terminaux B par des appels
à parseB et les terminaux token par l’appel
is TOKEN flux.
- Les filtrages se terminent obligatoirement par
la clause
| _ -> raise Error.
Si cette description vous semble un peu abstraite, vous pouvez dès
maintenant
consulter l’exemple d’analyseur de la figure 5.8.
Ces analyseurs parcourent l’entrée de la gauche vers la droite
pour construire implicitement une dérivation
gauche (comme précedemment), en ne se décidant qu’à la vue d’un unique lexème.
D’où le nom d’automate LL(1),
(Left-to-right parse, Leftmost derivation, (1-token lookahead))
La grammaire G est récursive à gauche, nous devons d’abord faire
disparaître cette récursion.
Il existe une procédure qui fonctionne toujours.
Son idée est de remplacer les productions de la forme
A → Aα1 ∣ … ∣ Aαn ∣ β1 ∣ …
βm (où aucun βj ne commence par A), par deux groupes de
productions :
À condition que tous les αi soient différents de є
(il n’existe pas de production A → A, peu productive de toute
façon et donc éliminable),
on fabrique une grammaire équivalente et qui n’est plus récursive à
gauche.
Si nous appliquons cette transformation à une adaptation de G
tenant compte des priorités, nous obtenons
la grammaire G‴ (figure 5.7).
| Figure 5.7: Élimination de la récursion à gauche. |
En fait, l’élimination de la récursion gauche présentée ne suffit pas,
car une grammaire peut être cyclique ou récursive à
gauche de façon indirecte, c’est à dire qu’il existe des dérivations
non triviales de la forme A ⇒*Aα (α = є
pour le cycle).
Considérez par exemple la grammaire A → Bb ∣ b et B → Aa ∣
a.
La technique précédente se genéralise et dans tous les cas on peut
transformer une grammaire en une grammaire équivalente sans cycles ni
récursion à gauche.
À titre indicatif, les transformations suivantes règlent le cas de l’exemple :
| A → Bb ∣ b B → Aa ∣ a | |
| A → b A → Aab ∣ ab B → Aa ∣ a | substitution de B selon ses productions |
| A → Aab ∣ b ∣ ab | production B inutile (départ en A) |
| A → bA′ ∣ abA′
A′ → abA′ ∣є | élimination de la récursion gauche de A
|
|
Bon, revenons à notre grammaire G‴ et à notre pouvoir d’analyse
limité,
nous devons maintenant au vu d’un seul lexème nous décider parmi
toutes les productions possibles associées à un non-terminal donné.
Pour ce faire introduisons une fonction FIRST définie des
mots α vers les ensembles de non-terminaux
et telle que a ∈ FIRST(α) si et seulement si
il existe une dérivation de la forme α ⇒*aβ.
Autrement dit, FIRST(α) est l’ensemble des non-terminaux qui
peuvent se trouver en tête d’une chaîne dérivée à partir de α.
Dès lors, si pour une production A → α1 ∣ …
αn, les ensembles FIRST(α1), … ,
FIRST(αn) sont deux à deux disjoints, nous saurons nous
décider pour un αi particulier.
Par exemple, dans le cas de la grammaire
G″ on a immédiatement
FIRST(( E )) = { ( } et
FIRST(int) = { int },
nous saurons donc le moment venu d’analyser un F choisir entre
utiliser la production F → ( E ) (on voit ()
ou la production F → int (on voit int), ou
signaler une erreur (dans tous les autres cas).
De même FIRST(F T0) = FIRST(F) =
FIRST(( E )) ∪ FIRST(int) = {(, int}.
Et donc, une tentative d’analyser un T se solde par une analyse d’un
F, suivie d’un T0 si on voit ( ou int, et par une
erreur sinon.
Mais cette belle simplicité se gâte avec T0,
on trouve bien
FIRST(* F T0) et FIRST(/ F T0) disjoints mais
rien ne nous permet de décider sur le champ entre la production
T0 → є (analyse de int eof par exemple) et une erreur
(analyse de int int, commencée en T).
Le cas général doit donc sérieusement considérer є.
Et de fait nous avons posé
FIRST(F T0) = FIRST(F) ce qui est ici exact mais
ce qui serait faux si on pouvait avoir F ⇒*є.
Par ailleurs, comme nous venons de le voir l’information fournie par
FIRST ne suffit pas à trancher le cas des productions de la forme
A → є.
Pour traiter le cas général, on définira FIRST vers
Σ ∪ {є},
l’intention étant que є ∈ FIRST(α) traduit
l’existence d’une dérivation α ⇒*є.
| | | FIRST(A) = FIRST(α1) ⋃ … ⋃
FIRST(αn), si les productions de A sont
A → α1 ∣ … ∣ αn |
|
| FIRST(Γα) = FIRST(Γ), si є ∉FIRST(Γ) |
| | FIRST(Γα) = (FIRST(Γ)∖ { є }) ⋃
FIRST(α), si є ∈ FIRST(Γ)
|
|
Ces règles suffisent pour calculer FIRST pour tous les
non-terminaux de la grammaire, par point fixe.
Il nous faut ensuite, pour régler le cas des
productions A → є,
calculer une nouvelle information.
Nous pouvons nous servir de l’ensemble FOLLOW(A)
des non-terminaux qui peuvent, dans les mots intermédiares d’une
dérivation, se trouver juste après un non-terminal A.
Clairement, une production A → є peut s’appliquer
quand le lexème courant est dans FOLLOW(A).
Pour définir FOLLOW de façon plus effective, nous pouvons adopter les
règles suivantes, support d’un éventuel calcul par point fixe.
De chaque décomposition possible de chaque production, une contrainte
à satisfaire par FOLLOW est déduite et FOLLOW doit remplir
toutes les contraintes possibles :
| Production | | Contrainte |
| A → αBβ | | (FIRST(β)∖ {є}) ⊆ FOLLOW(B) |
| A → αB | | FOLLOW(A) ⊆ FOLLOW(B) |
| A → αBβ, avec є ∈ FIRST(β) | | FOLLOW(A) ⊆ FOLLOW(B)
|
|
Pour exploiter FIRST et FOLLOW, il est pratique de construire
une table d’analyse prédictive.
Les lignes de cette table sont indicées par les non-terminaux et ses
colonnes par les terminaux.
Les cases contiennent des mots α.
On remplit la ligne A de la table avec les membre droits de ses
productions de la façon suivante :
-
Pour toutes les productions A → α,
mettre α dans les case de la
la colonne a pour tous les a de FIRST(α).
- En outre, si є est dans FIRST(α),
mettre α dans les cases de la colonne a pour tous
les a de FOLLOW(A).
Si, après examen de toutes les productions, aucune case ne contient plus
d’un élément, alors notre analyseur est écrit :
les cases vides donneront lieu à des erreurs, les cases ne contenant
qu’une entrée, à la poursuite de l’analyse.
Pour fixer les idées voici les fonctions FIRST, FOLLOW et la
table dans le cas de la grammaire G‴.
| | FIRST | FOLLOW |
| S | (, int | |
| E | (, int | ), eof |
| E0 | є, +, - | ), eof |
| T | (, int | ), +, -, eof |
| T0 | є, *, / | ), +, -, eof |
| F | (, int | ), +, -, *, /, eof
|
|
| | | int | ( | ) | + | - | * | / | eof |
| S | E eof | E eof | | | | | | |
| E | T E0 | T E0 | | | | | | |
| E0 | | | є | + T E0 | - T E0 | | | є |
| T | F T0 | F T0 | | | | | | |
| T0 | | | є | є | є | * F T0 | / F T0 | є |
| F | int | ( E ) | | | | | | |
|
|
L’analyseur est enfin donné par la figure 5.8.
Le code a le cachet du code engendré automatiquement, un certain
nombre d’optimisations évidentes sont possibles.
Ceci ne doit pas nous cacher que la table d’analyse prédictive
peut être utile quand on écrit un analyseur à la main.
| Figure 5.8: Un analyseur LL(1) des expressions arithmétiques |
| let rec start flux = match look flux with
| INT _|LPAR -> expr flux ; is EOF flux
| _ -> raise Error
and expr flux = match look flux with
| INT _|LPAR -> term flux ; expr0 flux
| _ -> raise Error
and expr0 flux = match look flux with
| ADD -> is ADD flux ; term flux ; expr0 flux
| SUB -> is SUB flux ; term flux ; expr0 flux
| RPAR|EOF -> ()
| _ -> raise Error
and term flux = match look flux with
| INT _|LPAR -> facteur flux ; term0 flux
| _ -> raise Error
and term0 flux = match look flux with
| MUL -> is MUL flux ; facteur flux ; term0 flux
| DIV -> is DIV flux ; facteur flux ; term0 flux
| RPAR|EOF|ADD|SUB -> ()
| _ -> raise Error
and factor flux = match look flux with
| INT i -> is (INT i)
| LPAR -> is LPAR ; expr flux ; is RPAR flux
| _ -> raise Error |
Si la construction de l’analyseur échoue, alors la grammaire G
présentée n’est pas LL(1).
Cela peut provenir d’une grammaire ambigüe
(car toutes les grammaires LL(1) sont non-ambigües) mais pas
forcément.
Construisons par exemple la table de la grammaire G″
(figure 5.3) qui nous avait servi de point de départ pour
écrire un analyseur à la main, en oubliant soustraction et division :
| | int | ( | ) | + | * | eof |
| S | E eof | E eof | | | | |
| E | T, T + E | T, T + E | | | | |
| T | F, F * T | F, F * T | | | | |
| F | int | ( E ) | | | | |
|
|
Certaines cases contiennnent deux mots,
la grammaire G″ n’est donc pas LL(1).
Pourtant, G″ est non-ambigüe.
Mais ici (ce n’est évidemment pas vrai en général) les mots qui
occupent la même case ont un préfixe (non-vide) commun,
par exemple T pour T et T + E.
On peut factoriser ce préfixe commun
en remplaçant les deux productions E → T ∣ T + E par
trois productions E → T E0 et
E0 → є ∣ + E.
Ce procédé de factorisation gauche est général.
Ici la grammaire résultante et la table seront :
| | int | ( | ) | + | * | eof |
| S | E eof | E eof | | | | |
| E | T + E0 | T + E0 | | | | |
| E0 | | | є | + E | | є |
| T | F * T0 | F * T0 | | | | |
| T0 | | | є | | * T | є |
| F | int | ( E ) | | | | |
|
|
La grammaire transformée est donc LL(1).
Notons que pour écrire un analyseur prédictif à la main,
la transformation n’est pas strictement nécessaire. Il suffit de se
donner le pouvoir d’examiner les lexèmes à l’intérieur du corps des
fonctions.
De fait, l’analyseur de la figure 5.4 est moralement
LL(1), modulo la détection des erreurs transformée en lecture du plus
long préfixe possible correct dans le flux.
Dans le cas plus général des grammaires des langages de programmation,
élimination de la récursion gauche et factorisation gauche ne
suffisent pas toujours pour produire une grammaire LL(1) et donc un
analyseur ; et ceci même lorsque la grammaire de départ est
non-ambigüe.
Par ailleurs, ces transformations sont peu pratiques lorsque l’on veut
un analyseur qui produit un arbre de syntaxe abstraite.
On généralise le principe de l’examen d’un
lexème à celui de k lexèmes. Les tables qui en résultent sont
potentiellement énormes et cette technique LL(k) n’est pas utilisée en
pratique. Dans un analyseur écrit à la main, on ne se privera pas
d’examiner plus d’un lexème dans certains cas particuliers, tout en
restant prudent.
5.4 Analyse montante (bottom-up parsing)
Autant la technique LL peut nous guider lors de l’écriture
d’analyseurs, autant elle n’est pas adaptée à la production
automatique d’analyseurs (puissance réduite, transformations de la
grammaire nécessaires).
Heureusement, il existe une autre technique dite LR(1), qui procède
toujours en lisant les lexèmes de gauche à droite (d’où le L),
cherche cette fois une dérivation droite (d’où le R)
et se décide au vu d’un lexème d’avance (d’où le 1).
5.4.1 Automates shift-reduce
Dans la présentation traditionelle de l’analyse montante, une certaine
sorte d’automate est chargé de l’analyse.
Les automates de ce style consomment un mot dans un flux et utilisent une pile
auxiliaire de symboles de la grammaire, ils peuvent procéder à deux actions :
-
shift, ie. consommer et empiler un lexème, ou
- reduce, ie. réduire une production.
Cela revient à appliquer une production sur le sommet (partie
droite) de la pile.
L’automate démarre avec une pile vide, procède à ses actions comme il
l’entend, jusqu’à se retrouver bloqué. Alors, si la pile contient le
symbole de départ et lui seul, il y a succès, sinon il y a échec.
Grâce au
renversement opéré par la pile, ces automates procèdent à l’analyse
selon une dérivation droite.
Pour s’en convaincre, considérons
comment un tel automate produit les deux dérivations droites possibles
du mot de non-terminaux 1 + 2 * 3 dans la grammaire ambigüe G
(figure 5.1) des
expressions arithmétiques (deux premiers examples de la
figure 5.9).
| Figure 5.9: Fonctionnnement de l’automate shift-reduce |
| Pile | Flux | Action | Production | Mot |
| | 1 + 2 * 3 | shift | | • 1 + 2 * 3 |
| 1 | + 2 * 3 | reduce | E → int | 1 • + 2 * 3 |
| E | + 2 * 3 | shift | | E • + 2 * 3 |
| E + | 2 * 3 | shift | | E + • 2 * 3 |
| E + 2 | * 3 | reduce | E → int | E + 2 • * 3 |
| E + E | * 3 | | | E + E • * 3 |
| E + E * | 3 | shift | | E + E * • 3 |
| E + E * 3 | | reduce | E → int | E + E * 3 • |
| E + E * E | | reduce | E → E * E | E + E * E • |
| E + E | | reduce | E → E + E | E + E • |
| E | | | | E |
|
| | Pile | Flux | Action | Production | Mot |
| | 1 + 2 * 3 | shift | | • 1 + 2 * 3 |
| 1 | + 2 * 3 | reduce | E → int | 1 • + 2 * 3 |
| E | + 2 * 3 | shift | | E • + 2 * 3 |
| E + | 2 * 3 | shift | | E + • 2 * 3 |
| E + 2 | * 3 | reduce | E → int | E + 2 • * 3 |
| E + E | * 3 | | E → E + E | E + E • * 3 |
| E | * 3 | shift | | E • * 3 |
| E * | 3 | shift | | E * • 3 |
| E * 3 | | reduce | E → int | E * 3 • |
| E * E | | reduce | E → E * E | E * E • |
| E | | | | E |
|
|
| Pile | Flux | Action | Production | Mot |
| | 1 + 2 * 3 | shift | | • 1 + 2 * 3 |
| 1 | + 2 * 3 | reduce | F → int | 1 • + 2 * 3 |
| F | + 2 * 3 | reduce | T → F | F • + 2 * 3 |
| T | + 2 * 3 | reduce | E → T | T • + 2 * 3 |
| E | + 2 * 3 | shift | | E • + 2 * 3 |
| E + | 2 * 3 | shift | | E + • 2 * 3 |
| E + 2 | * 3 | reduce | F → int | E + 2 • * 3 |
| E + F | * 3 | reduce | T → F | E + F • * 3 |
| E + T | * 3 | | | E + T • * 3 |
| E + T * | 3 | shift | | E + T * • 3 |
| E + T * 3 | | reduce | F → int | E + T * 3 • |
| E + T * F | | reduce | T → T * F | E + T * F • |
| E + T | | reduce | E → E + T | E + T • |
| E | | | | E • |
|
|
Pour retrouver les dérivations, il suffit, de procéder à l’envers de
l’analyse,
le mot intermédiaire à chaque étape est la concaténation de la pile et
du flux et
on applique la production utilisée à chaque étape reduce au sous-mot
correspondant au sommet de la pile (la limite entre pile et flux est
indiquée par •).
On peut aussi remplacer les non-terminaux de la pile par les arbres de
dérivation qui leur correspondent.
On voit alors clairement que l’arbre final est construit à partir des
feuilles et de la gauche vers la droite, le renversement opéré pour
retrouver la dérivation expliquant que cette dernière est droite.
L’étape cruciale qui détermine le choix de l’une ou l’autre des
dérivations droites est signalée (un shift de * contre un
reduce de E → E + E).
Si nous levons l’ambiguïté en transformant la grammaire,
alors seule une de ces deux étapes sera possible.
Pour comprendre comment l’automate peut se décider à coup sûr entre shift et
reduce, il vaut mieux s’affranchir de cette ambigüité.
Donnons nous donc la grammaire non-ambigüe G′ des expressions
arithmétiques (avec les productions E → E + T et
T → T * F entre autres), et examinons
comment l’automate reconnaît 1 + 2 * 3 selon cette grammaire
(dernier exemple de la figure 5.9).
Il apparaît alors clairement d’abord que tous les entiers sont d’abord
shiftés (empilés), puis réduits.
Mais l’entier 1 est réduit en E (en trois étapes), tandis que
2 est réduit en T et 3 seulement en F.
C’est certainement le bon choix dans tous les cas, car sinon, il y
aurait une erreur plus tard.
La dernière de ces décisions ne s’explique certainement pas uniquement
par la fin du flux
(car la réduction à E s’impose dans le cas d’un seul entier dans
l’entrée). En revanche, on la comprend mieux si on examine la pile
au moment de choisir de réduire trois symboles selon T → T *
F plutôt qu’un seul selon T → F : le sommet de pile, invite
l’automate à en faire le maximum.
Remarquons aussi, à l’étape cruciale (distinguée), que la présence de
* en tête du flot invite à ne pas réduire E + T en attente
sur la pile.
5.4.2 Programmation en Caml d’un analyseur montant
L’intervention d’un automate obscurcit un peu le propos.
Comme pour l’analyse descendante on se propose donc d’écrire
quelques analyseurs à la main avant d’automatiser le procédé.
On considère une fois encore une grammaire ambigüe des expressions
arithmétiques en la simplifiant beaucoup:
On aura besoin d’un type de tous les symboles de la grammaire, le
voici:
| type symbol = E | Terminal of token |
L’automate shift/reduce sera réalisé par une bête fonction recursive,
qui se décicidera au vu du premier lexème et de la pile de symboles
(ou plus exactement de quelques éléments de son sommet) :
auto, de la forme:
| let rec auto stack flux = match look flux, stack with
(* Accepter l'entrée (qui est finie) *)
| EOF, [E] -> ()
…
(* Petite fonction pour éviter d'écrire 10 fois la même chose *)
and shift stack flux =
let tok = look flux in
eat flux ;
auto (Terminal tok::stack) flux |
La grammaire est simplifiée mais elle presente encore une
ambiguité typique de la grammaire de départ.
En effet, on peut voir E + E + E comme
(E + E) + E ou comme E + (E + E).
Lors de l’analyse, le choix va se poser
quand on aura déja reconnu E + E et que le premier
lexème du flux est +.
Pour obtenir la première inteprétation il faudra réduire, tandis que
pour obtenir la seconde interpétation il faudra shifter.
Nous décidons par exemple de faire pencher les arbres à gauche,
c’est à dire que E + E + E s’interprète comme
(E + E) + E.
Nous aurons donc la règle :
| let rec auto stack flux = match look flux, stack with
…
(* Reduction de E → E + E *)
| ADD, E::Terminal ADD::E::rem -> auto (E::rem) flux
… |
Par ailleurs, si le sommet de la pile n’est pas de la forme ci-dessus,
il faut shifter le terminal « + ».
| | ADD, _ -> shift stack flux |
Mais, compte tenu de la nature de la grammaire, on peut préciser ce
que l’on entend par « toutes les autres situations ».
Ici, E sera tout seul sur la pile. On écrira donc plutôt.
| | ADD, [E] -> shift stack flux |
Interessons nous maintenant aux entiers. Dans toutes les situations il
faut les shifter, puis les réduire. On serait donc tenté d’écrire:
| | INT _, _ -> shift stack flux
| _, Terminal (INT _)::rem -> auto (E::rem) flux |
Mais ici encore, on souhaite être beaucoup plus précis.
| | INT _, (Terminal ADD::E::_|[] ->) shift stack flux
| (ADD|EOF), Terminal (INT _)::rem -> auto (E::rem) flux |
Bref, voici la fonction auto complète.
| let rec auto stack flux = match look flux, stack with
(* Que faire avec un seul E ? *)
| EOF, [E] -> ()
| ADD, [E] -> shift stack flux
(* Réduction de E → E + E *)
| (ADD|EOF), E::Terminal ADD::E::rem -> auto (E::rem) flux
(* Réduction de E → int *)
| (ADD|EOF), Terminal (INT _)::rem -> auto (E::rem) flux
(* Shift de int *)
| INT _, (Terminal ADD::E::_|[]) -> shift stack flux
(* N'importe quoi d'autre est une erreur *)
| _ -> raise Error |
Nous choisissons maintenant de compliquer un peu notre grammaire, en
lui ajoutant une production E → ( E ).
En refléchissant aux couples premier symbole du flux, sommet de la
pile on obtient finalement cet automate :
| let rec auto stack flux = match look flux, stack with
(* Ouf ! *)
| EOF, [E] -> ()
| (ADD|EOF|RPAR), E::Terminal ADD::E::rem -> auto (E::rem) flux
| ADD, ([E]|E::Terminal LPAR::_) -> shift stack flux
| INT _, (Terminal ADD::E::_|Terminal LPAR::_|[]) -> shift stack flux
| (ADD|EOF|RPAR), Terminal (INT _)::rem -> auto (E::rem) flux
(* Avec des parenthèses *)
| RPAR, E::Terminal LPAR::_ -> shift stack flux
| (ADD|RPAR|EOF), Terminal RPAR::E::Terminal LPAR::rem -> auto (E::rem) flux
| LPAR, (Terminal ADD::E::_|Terminal LPAR::_|[]) -> shift stack flux
(* N'importe quoi d'autre est une erreur *)
| _ -> raise Error |
Bon, nous sommes arrivés à construire un analyseur shift/reduce à la
main. Mais il est clair que ce sera difficile dans le cas général.
Par ailleurs on souhaite éviter les analyses répétées de la pile
(même si elles sont particulièrement faciles à programmer en Caml).
5.4.3 Analyse LR(1)
Dans les deux sections précédentes nous avons argumenté qu’un
analyseur LR se décidait au vu du lexème en tête du flux et d’une
fraction de sa pile (vers le sommet)
L’idée de base des analyseurs LR(1)
est d’assurer le contrôle de l’automate shift-reduce à l’aide d’un
automate fini.
Un état donné représente donc un état d’avancement de l’analyse.
Dans le cadre qui nous intéresse cet état est représente par
un ensemble de productions pointées, de la forme
A → α • β où
A → αβ est une production de la grammaire.
Reprenons par exemple le cas de la grammaire:
Initialement on a rien empilé, et on veut reconnaître E eof.
L’état initial contient donc S → • E eof.
Pour identifier E dans le flux, nous devons identifier l’un des
membre droits des productions de E. Soit un état initial numéro 0:
| {
S → • E eof,
E → • E + E,
E → • int,
E → • ( E )
}
|
Le procédé appliqué dit de fermeture est décrit précisément par la
suite. Il revient à ajouter toutes les productions pointées
A → •α dès que … → … • A …
apparaît dans l’état.
Admetons maintenant que E a été reconnu, la pile contiendra donc
un E et, compte tenu de notre état initial le flux sera eof ou
+ E.
Soit un état numéro 1 (déjà fermé) :
| { S → E • eof,
E → E • + E }
|
Pour pouvoir passer le contrôle à cet état après la
reconnaissance de E dans le flux initial, on utilise la pile de
l’automate shift-reduce, c’est à dire que lorsque l’automate passe
dans un état quelconque, cet état est systématiquement empilé,
en même temps que le symbole de la grammaire qui était empilé aux
sections précédentes.
Ici on doit donc supposer que l’état 0 est déjà sur la pile.
Ainsi, lorsque l’automate effectuera plus tard l’ultime action reduce
qui empile E il trouvera l’état initial sur la pile et saura
effectuer une transition de l’état initial à l’état ci-dessus.
Mais pour le moment E n’est pas reconnu, supposons que le flux débute
par un entier, alors cet entier est shifté et l’automate passe dans
l’état numéro 2 suivant (qui est également empilé)
Le point est à la fin, nous pouvons réduire (en fait il faudrait à
priori regarder le premier lexème du flux, qui ici doit être +
ou eof, mais bon).
La réduction revient ici à dépiler int et à empiler E à la
place, l’état E → int • est dépilé et on assure la
transition vers l’état 1 en fonction de l’état en sommet de pile
(ici l’état 0) et du non-terminal reconnu (ici E).
L’état numéro 1 est maintenant en sommet de pile et il saura quoi
faire selon le premier lexème du flux
(annoncer une reconnaisance réussie en cas de eof, shifter
un + ou signaler une erreur autrement).
Voici maintenant le procédé genéral de construction de l’automate de
contrôle.
Soit une grammaire dont le symbole
de départ est Sg.
Le symbole de départ de la grammaire considérée ensuite
est un nouveaux non-terminal S. On ajoute également
une production un peu spéciale → S dite axiome,
ainsi qu’une production S → Sg $,
où $ est un non-terminal réservé pour signaler la fin de l’entrée.
L’automate shift-reduce est raffiné en un automate LR :
-
Il y a en fait quatre actions,
shift, reduce(A → α) (la production réduite est
indiquée), accept (succès) et error (échec).
- La pile est maintenant
composée de couples (Δi, si) d’états et de symboles de la
grammaire, sauf le fond de pile s0 qui est seulement l’état
initial de l’automate.
- L’automate est déterminé par deux fonctions :
-
goto(s,Δ) vers les états, ce sont les transitions de
l’automate de contrôle, indicées par tous les symboles de la grammaire.
- Et action(s,a) vers les actions, ce sont des actions de
l’automate shift-reduce, commandées par l’automate de contrôle au vu
du premier lexème du flux.
Si sa pile est s0, (Δ1), …
(Δm, sm), l’automate consulte le lexème a en attente et par cas
sur la valeur de action(sm, a) effectue les actions suivantes.
-
shift
-
Le lexème est consommé et (a, goto(sm, a)) est empilé.
- reduce(A → α)
-
L’automate dépile l eléments, où l est la longueur de α et
(A, goto(sm−l, A)) est empilé.
- accept ou error
-
L’automate signale le succès ou un échec et s’arrête.
Remarquez que, en cas de shift, une transition de l’automate de
contrôle est effectuée et que l’état atteint est empilé.
En cas de reduce, l’état courant de l’automate de contrôle est oublié
et on opère de même, cette fois à partir de l’état qui prévalait avant
d’engager la reconnaissance de la production réduite.
Un état I de l’automate de contrôle est un ensemble de configurations C.
une configuration C est une paire composée,
-
d’une production pointée A → α • β,
où A → αβ est une production,
- et du prochain lexème possible a après αβ.
Une configuration C décrit un état courant de l’automate
shift-reduce sous-jacent, avec
α en sommet de pile et un flux dont le début
dérive de βa.
La fermeture d’un ensemble de configurations I est le plus petit ensemble
contenant I et satisfaisant
⎛
⎝ |
(A → α • B β, a) ∈ I
∧ B → γ ∈ G
∧ b ∈ FIRST (β a)
| ⎞
⎠ | ⇒ (B →• γ, b) ∈ I
|
L’intuition est que nous cherchons à identifier (en un même état de
l’automate de contrôle) certaines
configurations de l’automate shift-reduce.
Dans une configuration A → α•Bβ,
une partie α
est déjà reconnue et une autre Bβ devrait l’être.
Donc, il faut certainement
s’attendre à reconnaître aussi γ pour toutes les productions
B → γ ;
la deuxième partie de la configuration sert à affiner cette
première règle à l’aide des non-terminaux qui peuvent se trouver
après B (FIRST(βa) ne peut pas contenir є) et donc
après γ.
L’ajout du symbole a augmente sensiblement le pouvoir discriminant
des états, notamemt dans le cas des productions complètement reconnues
(de la forme A → α •).
Les transitions sont définies ainsi :
| goto (I,Δ) =
fermeture
(
{(A → α Δ • β, a) ∣ (A → α • Δ β, a) ∈ I}
)
|
Autrement dit, on passe de I à J en faisant avancer de point •
d’un cran. Le symbole Δ change de statut il prend maintenant
part à un membre droit de production reconnu.
Notons que si Δ est un non terminal a, alors l’automate
shift-reduce devra effectuer un shift. Et que dans tous les cas
l’automate ce contrôle effectue une transition de I à J.
L’autre cas, (Δ est un non-terminal A) correspond à la
transition de l’automate de contrôle à effectuer après la réduction
d’une production de membre gauche A.
L’état initial est la fermeture de { ( → • S, a) ∣ a
∈ Σ }. Les
états sont les ensembles de configurations fermées non-vides atteignables
par une suite de transitions arbitraires à partir de l’état initial.
Cette construction ressemble fort, en plus compliqué dans les détails,
à la déterminisation d’un automate fini dont les états
seraient les configurations.
Une fois construit le graphe décrit ci dessus, on en tire action.
-
Si (A → α • a β, b) ∈ I
et goto (I, a) = J,
alors action (I,a) = shift
(on peut représenter simultanément goto(I,a) en écrivant shift(J)).,
- Si (A → α •, a) ∈ I, alors
action (I,a) = reduce (A → α).
Sauf, si A → α est l’axiome → S, auquel cas
action (I,a) = accept.
Si action(I,a) n’est pas défini par ces deux règles, alors on a
action(I,a) = error.
Si il y a des conflits, c’est à dire
plusieurs valeurs possibles pour action (I,a), alors la
grammaire G n’est pas LR(1).
Cela peut provenir d’une grammaire ambigüe mais aussi (plutôt rarement en
pratique) d’une grammaire non-ambigüe suffisamment compliquée.
En pratique, les fonctions action et goto sont réalisées par des tables,
des états de l’automate de contrôle par les symboles de la grammaire
pour action, et des états par les non-terminaux pour goto.
Ces tables seront normalement assez creuses et peuvent compactées.
| Figure 5.10: exemple de graphe des états LR(1) |
Sans détailler plus avant, la figure 5.10
donne le graphe pour la grammaire suivante des sommes et des différences
arithmétiques (symbole de départ E) :
Dans les états, notez la notation des configurations de même
productions pointée en une seule ligne montrant un ensemble de
prochains lexèmes possibles. Voir aussi l’animation Postscript de la construction
du graphe, dans la version web du cours.
Dans cette figure, on constate que l’on
peut enlever la seconde partie des configurations,
les ensembles de productions pointées suffisent à définir les états.
Les générateurs d’analyseurs grammaticaux les plus répandus
(yacc, bison, etc.)
ne suivent pas exactement la constructions des tables LR(1), car ces
tables sont de taille importante en pratique.
Le graphe est construit comme dans le cas LR(1), mais on efface
ensuite les ensembles de prochains lexèmes possibles des états et on
fusionne les états ainsi identifiés avant
de construire les tables de l’analyseur.
Les tables sont alors plus petites, tandis que la puissance de
compilation n’est pas excessivement diminuée.
Cette technique est dénommée LALR(1) (pour Look-Ahead LR(1)).
Si la production des tables s’opère sans conflit, la grammaire
compilée est dite LALR(1).
Enfin, on définit assez naturellement les grammaires LR(k) en
considérant les automates de contrôle qui se decident à l’aide de k
lexèmes d’avance. Les tables deviennent potentiellement énormes.
Du point de vue du la puissance de toutes les techniques vues, on a
les relations suivantes, où l’acronyme de chaque technique désigne
l’ensemble des grammaires qu’elle peut traiter.
Toutes les grammaires citées sont non-ambigües.
Compte tenu de la description donnée dans ce cours, l’inclusion
LL(1) ⊂ LR(1) se comprend, si on considère qu’un
automate LR(1) dispose de plus d’informations qu’un
programme LL(1).
Les programmes doivent deviner le membre droit à choisir en fonction
d’un lexème d’avance, tandis
que l’automate ne prend réellement sa décision qu’une fois que le membre
droit est en pile, en fonction toujours du lexème d’avance.
Cette remarque ne remplace bien entendu pas une démonstration.
Dans la pratique, les langages de programmation ont des grammaires
LALR(1) et leurs tables sont de taille raisonnable.
Réciproquement, comme les générateurs d’analyseurs disponibles
reposent sur la technique LALR(1), les langages de programmation
tendent à avoir des grammaires LALR(1).
Les grammaires LL ne sont par pour autant absentes des langages de
programmation.
-
Pascal a une grammaire essentiellement LL(2?).
On y arrive assez facilement en faisant débuter les instructions par des
mots-clés différents et en exigeant des constructions fermées
(typiquement begin… end, var…
begin). Pour les expressions, le problème des opérateurs est
soluble en pratique, car bien balisé.
Pascal a été conçu dans cet esprit.
- Il existe des outils plus souples que les compilateurs traditionnels
de grammaires, tels camlp4, reposant sur les grammaires LL,
quand même plus simples à comprendre.
L’utilisation d’un outil de compilation des grammaires en analyseurs
a principalement deux avantages, d’une part l’écriture des analyseurs
(et surtout leur modification)
devient facile, d’autre part, les conflits détectés proviennent le
plus souvent de grammaires ambigües qui sont donc détectables
facilement.
L’outil ocamlyacc transforme un fichier source
Nom.mly contenant une description de grammaire, en
deux fichiers Nom.ml et
Nom.mli contenants l’analyseur grammatical.
En effet la description de la grammaire comprend celle de ses
non-terminaux, cette dernière est traduite en un type des lexèmes, de nom
conventionnel token.
Le fichier Nom.mli exporte ce type des lexèmes, au
profit de l’analyseur lexical.
Pour chaque symbole de départ S, l’analyseur sera une fonction
homonyme prenant en argument un analyseur syntaxique de
type (Lexing.lexbuf -> Nom.token) et un flux
de type Lexing.lexbuf.
| Figure 5.11: Un exemple arith.mly de source ocamlyacc |
| %{
open Ast
%}
/* Déclaration des lexèmes */
%token LPAR RPAR
%token ADD SUB MUL DIV
%token <int> INT
%token EOF
/* Point d'entrée */
%start expr
%type <Ast.t> expr
%%
expr:
expr1 EOF {$1}
;
expr1:
expr1 ADD expr1 {Binop (Add,$1, $3)}
| expr1 SUB expr1 {Binop (Sub,$1, $3)}
| expr1 MUL expr1 {Binop (Mul,$1, $3)}
| expr1 DIV expr1 {Binop (Div,$1, $3)}
| SUB expr1 {Binop (Sub, Int 0, $2)}
| INT {Int $1}
| LPAR expr1 RPAR {$2}
; |
La figure 5.11 donne un exemple de spécification de grammaire
pour ocamlyacc. Il s’agit encore une fois de la grammaire
ambigüe des expressions arithmétiques, (avec la négation ou moins
« unaire » en plus) ; l’intention est ici d’écrire
un analyseur syntaxique qui rend un arbre de syntaxe abstraite (de
type Ast.t).
Cet exemple fait apparaître les trois sections des fichiers .mly.
-
La première section, de
%{ à }%, dite prélude,
contient du code source Caml, à mettre en tête du fichier .ml
produit. Ici on se contente d’ouvrir le module Ast, réputé
contenir la définition du type des arbres de syntaxe abstraite.
| type t = Int of int | Binop of binop * t * t
and binop = Add | Sub | Mul | Div |
- Ensuite vient une section de déclarations destinées à
ocamlyacc, il s’agit ici de la déclaration des lexèmes
(notez la syntaxe tordue de la déclaration du lexème
INT qui prend un argument entier), puis
du point d’entrée et de son type.
Cette section se termine avec le mot-clé (de ocamlyacc)
%%.
On notera que les commentaires de cette section sont ceux de C
(/* … */). En effet, ocamlyacc est
essentiellement yacc, qui est plutôt orienté
vers C. - Enfin, vient la section qui définit les productions de la
grammaire, on prendra un peu garde à la syntaxe, le non-terminal est
suivi de « : » ses membres droits sont séparées par «
| » et
le dernier membre droit est suivi de « ; ». Une production
vide, se note par un membre droit vide (il n’y en a pas ici).
Les actions sont données entre accolades, à raison d’une par membre
droit, elles sont évaluées si le membre droit est réduit et
constituent la valeur du non-terminal correspondant.
Ici, les actions consistent comme souvent à construire l’arbre de
syntaxe abstraite. Dans une action, on peut faire référence aux
valeurs des symboles du membre droit par un entier préfixé de
« $ ». Ces valeurs sont les résultats de l’analyse des non-terminaux et l’argument des
terminaux pour ceux qui en ont un, comme montré par la production E → int.
La compilation par « ocamlyacc arith.mly » se solde par
« 20 shift/reduce conflicts ».
Et c’est bien normal, car la grammaire est assez ambigüe.
Un analyseur est quand même produit, ocamlyacc « résolvant »
les conflits selon ses règles (shift gagne sur reduce, et entre
deux reduce, celui de la production qui apparaît en premier
dans le source gagne).
On ne peut pas laisser ocamlyacc resoudre les conflits pour
nous, sauf dans les rares cas où on comprend ce qui se passe et où on
estime que c’est satisfaisant.
L’automate produit et le détail des conflits sont donnés par un
fichier arith.output créé
par ocamlyacc si on lui passe l’option -v.
Mais ici, reportons nous d’abord aux deux premières exécutions de
l’automate à pile de la figure 5.9 qui, rapellons le, décrivent
deux dérivations de la même expression arithmétique dans la même
grammaire ou presque.
À l’étape critique signalée, les deux automates ont la pile
E + E et * est le lexème en tête du flux.
Selon les règles usuelles, il ne faut pas réduire la somme et *
doit être shifté.
Dans le fichier arith.output on trouve en particulier
le détail des conflits de la réduction des sommes
(attention, les entiers des shift sont des états de
l’automate, tandis que ceux des reduce sont des numéros
donnés aux productions) :
16: shift/reduce conflict (shift 10, reduce 2) on ADD
16: shift/reduce conflict (shift 11, reduce 2) on SUB
16: shift/reduce conflict (shift 12, reduce 2) on MUL
16: shift/reduce conflict (shift 13, reduce 2) on DIV
state 16
expr1 : expr1 . ADD expr1 (2)
expr1 : expr1 ADD expr1 . (2)
expr1 : expr1 . SUB expr1 (3)
expr1 : expr1 . MUL expr1 (4)
expr1 : expr1 . DIV expr1 (5)
On retrouve au passage les ensembles de productions prointées qui
définissent les états.
Un autre conflit intéressant apparaît, celui entre le shift de
+ et le reduce de la somme, issu de la confrontation entre les
deux premières productions pointées.
Cette ambigüité, dite d’associativité, se révèle sur le mot de la
grammaire E + E • + E à voir comme (E + E) + E (réduire) ou comme
E + (E + E) (shifter) ; et là, l’interprétation usuelle
commande de réduire.
Nous pourrions bien évidemment réécrire un peu la grammaire, mais
ocamlyacc fournit un mécanisme de priorité bien plus
pratique.
Nous pouvons associer des niveaux de priorité aux lexèmes
(plusieurs lexèmes peuvent avoir la même priorité).
Ces priorités s’étendent toutes seules aux productions, la
priorité d’une production étant celle de son dernier lexème.
Dans un conflit shift/reduce, les priorités du lexème à shifter et
de la production à réduire sont comparées, le plus fort gagne
(silencieusement).
Dans un conflit reduce/reduce, les priorités des deux règles sont
comparées. On voit alors que le système des priorités correspond à
l’intuition : la multiplication est plus prioritaire que l’addition.
Mais ce n’est pas tout, dans le cas du conflit d’associativité,
production et lexème ont la même priorité (celle de +).
Heureusement ocamlyacc autorise aussi de munir les niveaux de
priorité d’une associativité, à gauche (%left),
à droite (%right) ou interdite (%nonassoc).
Ces associativités entrent en jeu dans un conflit shift/reduce
quand les priorités du lexème et de la règle sont identiques.
Alors, si l’associativité est gauche, on va réduire, si
l’associativité est droite on va shifter, et si l’associativité est
interdite l’automate signalera que l’entrée est incorrecte.
Ici on veut donc associativité gauche (arbres qui penchent à gauche),
et deux niveaux de priorité (* et /, plus prioritaires que
+ et -). On
écrit donc, après la définition des lexèmes.
| /* Des moins prioritaires aux plus prioritaires */
%left ADD SUB
%left MUL DIV |
Modifions le fichier et recompilons,
les conflits disparaissent ou plus exactement ocamlyacc ne
les signale plus. Mais que se passe-t-il maintenant pour le
moins unaire ? Regardons donc dans le nouveau fichier
arith.output, où est réduite la production
E → - E (numéro 6) :
state 9
expr1 : expr1 . ADD expr1 (2)
expr1 : expr1 . SUB expr1 (3)
expr1 : expr1 . MUL expr1 (4)
expr1 : expr1 . DIV expr1 (5)
expr1 : SUB expr1 . (6)
MUL shift 12
DIV shift 13
. reduce 6
Il y a shift pour * et / et reduce pour tous les
autres lexèmes (« . » indique le comportement par défaut de l’automate).
C’est logique compte-tenu des priorités, - E • * E est
actuellement interprété comme - (E * E).
Or, tous ces conflits devraient se résoudre par un reduce :
- E • op E est à comprendre comme
(- E) op E.
Autrement dit, il faut rendre la production du moins unaire plus
prioritaire que les quatre opérateurs.
C’est possible en donnant un nom à un niveau de priorité et en forcant
la priorité de la production ainsi :
| %left ADD SUB
%left MUL DIV
%left UMINUS /* left sans importance ici, car pas de lexème de cette priorité */
...
| SUB expr1 %prec UMINUS {Binexp (Sub, Int 0, $2)} |
Une fois ces modifications faites, on peut s’amuser à vérifier que
l’automate se comporte correctement dans l’état 9. On voit que les
actions sont toutes de réduire : « . reduce 6 ».
La question demande reflexion, mais c’est surtout une question de
programmation. De fait, dans les fonctions expr et
term, on analyse l’arbre de dérivation qui penche à
droite en produisant l’arbre de syntaxe abstraite qui penche à gauche.
| type ast = Int of int | Binop of binop * ast * ast
and binop = Add | Sub | Mul | Div
let rec expr flux =
let t1 = term flux in
do_expr t1 flux
and do_expr t1 flux = match look flux with
| ADD ->
eat flux ;
let t2 = term flux in
do_expr (Binop (Add, t1, t2)) flux
| SUB ->
eat flux ;
let t2 = term flux in
do_expr (Binop (Sub, t1, t2)) flux
| _ -> t1
and term flux = do_term (factor flux) flux
and do_term t1 flux = match look flux with
| MUL ->
eat flux ;
let t2 = factor flux in
do_expr (Binop (Mul, t1, t2)) flux
| SUB ->
eat flux ;
let t2 = factor flux in
do_expr (Binop (Div, t1, t2)) flux
| _ -> t1
and factor flux = match look flux with
| INT i -> eat flux ; Int i
| LPAR ->
eat flux ;
let t = expr flux in
begin match look flux with
| RPAR -> eat flux ; t
| _ -> raise Error
end
| _ -> raise Error |
On comprendra peut-être mieux le programme si on regarde la
grammaire de la figure 5.7 en comprenant un E0 comme une
liste de T séparés par + ou -, et
un T0 comme une liste de F séparés par * ou /.











