Chapitre 3  Le langage Pseudo-Pascal

• Expressivité des langages de programmation
• Comment définir un langage
• Sémantique opérationnelle de la calculette
• Diverses constructions et leur sémantique
• Les fonctions
• Le langage Pseudo-Pascal (PP)

Avant de décrire les phases de notre compilateur une à une, en suivant l’ordre de leur application, il me paraît plus malin de commencer par décrire d’abord notre langage de programmation, en détaillant sa sémantique plutôt que sa syntaxe.

3.1  Expressivité des langages de programmation

Les langages de programmation sont les langages que l’être humain utilise pour dire à un ordinateur ce qu’il doit faire. On peut évoquer les catégories suivantes :

Langages généraux

Ils doivent être complets, ie. permettre d’exprimer tous les algorithmes calculables. Au minimum, il faut une mémoire réputée infinie (c’est à dire grande) et la possibilité d’exprimer la récursion (construction primitive ou boucle while). Ex: Fortran, Pascal, C, Caml, etc.

Langages spécialisés

(DSL pour Domain Specific Languages) Ce sont par exemple les langages pour le graphisme, pour commander des robots ou encore la calculette. Ils peuvent ne pas être complets.

Bien qu’ils permettent d’exprimer tous les calculs possibles, (c’est approximativement la thèse de Church), les langages généraux ne sont pas tous équivalents stricto-sensu. Ils se distinguent par leur expressivité, c’est à dire par leur capacité d’exprimer des algorithmes succinctement (et directement).

Par exemple, on peut toujours implémenter un algorithme récursif à l’aide d’une pile explicite (un tableau plus un indice), mais le langage qui offre la récursivité permet une implémentation plus concise et élégante.

Plus précisément, lorsque l’on se pose la question de l’expressivité d’un langage on peut examiner les points suivants :

Les fonctions

• Les fonctions peuvent être définies localement à d’autres fonctions, comme en Pascal, ou pas, comme en C.
• Les fonctions peuvent être des valeurs du langages comme en Caml (ou en C !), ou pas, comme en Pascal où une fonction ne peut pas rendre une autre fonction comme résultat.

Les structures de données Au delà des divers entiers et des tableaux la plupart des langages fournissent des produits (records de C et Pascal, paires de ML) et des sommes (enums et surtout unions de C, types dits concrets de ML). Lisp organise toutes ses données autour de la liste que l’on peut voir comme la somme de la liste vide (nil) et de la cellule de liste (cons). Certaines structures de données comme les chaînes (des tableaux de caractères de taille variable) ne semblent pas à première vue étendre beaucoup l’expressivité du langage, mais leur intérêt pratique apparaît très vite dès que l’on programme.

Les modules, les objets sont des traits qui autorisent la programmation incrémentale.

Le typage restreint l’expressivité au profit de la sécurité. On considérera d’abord le système de type du langage, par exemple en ML on dispose d’un polymorphisme dit générique qui n’existe pas en Java — en ML on pourra écrire une fonction identité qui accepte tous les arguments possibles, c’est impossible en Java.

On pourra aussi s’intéresser à l’impact du système de type sur la programmation : les types sont-ils construits par le compilateur comme en ML, essentiellement donnés par le programmeur comme en C, Pascal et Java, inexistant dans les programmes comme en Lisp et Basic, mais bien présents à l’exécution. Attention, contrairement à une opinion assez répandue, il existe très peu de langages absolument non-typés, à part peut être l’assembleur, on distinguera plutôt entre langages typés statiquement (ML, C, Pascal) : le compilateur vérifie que le programme est bien typé, l’exécution n’échoue jamais (ou rarement) ; et langages typés dynamiquement (Lisp, Basic) : le compilateur ne vérifie rien, mais l’exécution vérifie le bien fondé d’une opération avant de la réaliser. On notera que Java est peu les deux à la fois et on se gardera de trop conclure.

Note : Pour comparer l’expressivité formellement, il faut en général le faire point à point en exhibant un codage d’un langage dans un autre qui respecte certaines règles (compositionalité, localité, etc.)

3.2  Comment définir un langage

3.2.1  Syntaxe

La syntaxe décrit les mots et les phrases du langage. Elle ne donne aucun sens aux phrases.

On peut distinguer syntaxe concrète et syntaxe abstraite. La syntaxe concrète est le discours lui-même, en informatique c’est un fichier, mais on pourrait conceptuellement déclamer des programmes. C’est disons une suite de lettres qui forment des mots qui forment des phrases. La syntaxe abstraite est la structure du discours, en informatique c’est un arbre. Dans les compilateurs, le programme à compiler est bien un arbre, dans le discours sur le langage c’est un dessin. La grammaire est la définition de tous les arbres possibles c’est à dire de tous les discours syntaxiquement bien formés d’un langage.

En pratique il est bien commode de commencer par reconnaître les mots avant de s’attaquer aux phrases. On passe donc de la syntaxe concrète à la syntaxe abstraite en deux temps, d’abord par l’analyse lexicale qui traduit une suite de caractères en suite de mots puis par l’analyse grammaticale qui transforme une suite de mots en arbre de syntaxe abstraite.

L’exemple du langage des expressions arithmétiques éclairera un peu ces notions.

Commençons par définir les entiers, comme une suite de chiffres, les variables comme des suites de caractères alphabétiques, les blancs comme des suites d’espaces et quelques caractères particuliers comme des mots (« ( », « + », etc.) On exprimera les deux syntaxes à partir des mots ainsi définis.

Syntaxe concrète représentée par une grammaire, (dans le style dit BNF)

Dans ce style de description, on distingue les terminaux, qui sont les mots, et les non-terminaux qui sont les noms définis par la grammaire.

Syntaxe abstraite (en Caml) Représentée par le type expression.

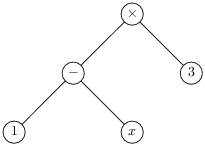
Exemple Ainsi les expressions « (1 - x) * 3 » et « (1-x)*(3) » ont la même syntaxe abstraite :

Les malins remarqueront que l’arbre ci-dessus est décrit sous forme de syntaxe (concrète !) Caml. On devrait donc plutôt dessiner un arbre :

On voit alors que le principal effet de l’analyse syntaxique est de remplacer une structure arborescente décrite à l’aide de parenthèses en cette structure elle-même.

La syntaxe concrète peut aussi permettre d’exprimer la même construction de syntaxe abstraite sous différentes formes. Ainsi, le caractère « A » peut être représenté par « 'A' » et « '\065' », ou plus significativement la construction de liaison de Caml(-Light) peut s’écrire « let d in e » ou « e where d ». Il convient en général de ne pas abuser de cette possibilité, car elle va contre le principe d’économie de moyens : à quoi bon donner deux façons d’exprimer la même chose ? En outre elle peut rendre les messages d’erreur du compilateur inintelligibles.

3.2.2  Sémantique

Il s’agit de donner un sens aux phrases. C’est beaucoup plus facile à faire dans le cas d’un langage de programmation que dans le cas de la langue naturelle. Il s’agit ici d’expliquer ce qu’un programme fait.

On distinguera en gros trois façons de procéder.

Sémantique informelle

Un document de référence décrit la sémantique. Ce document est écrit dans un langage technique qui fait appel à la culture informatique du lecteur. Voici par exemple la sémantique de la boucle while en C.

L’instruction while est de la forme :

while (expression) instruction

la sous-instruction est exécutée de manière répétée tant que la valeur de l’expression reste non nulle. On teste l’expression avant d’exécuter l’instruction.

L’avantage est bien entendu que la langue naturelle se prête bien aux vastes concepts et aux descriptions synthétiques et qu’elle est connue du lecteur. On notera ici le choix du mot reste, à mettre en rapport avec l’idée qu’une boucle peut être exécutée plusieurs fois et que la valeur d’une expression peut changer au cours du temps. L’inconvénient est le manque de rigueur, en particulier la fameuse culture informatique est en perpétuelle évolution et il n’est pas toujours évident de faire la part des concepts généraux (comme « un appel de fonction ») et des détails d’implémentation (comme « une adresse mémoire » ou « la zone de code »). En outre, il est impossible de faire des preuves satisfaisantes sans une description plus formelle. On pourrait par exemple vouloir prouver qu’une optimisation compliquée ne change pas les résultats d’un programme, ou qu’un programme bien typé n’échoue pas lors de l’exécution.

Sémantique dénotationnelle

C’est exactement le contraire de la précédente, on cherche à associer à un programme un objet construit selon les règles de l’art mathématique. Les valeurs d’un langage sont généralement modélisées comme des treillis, les fonctions comme des fonctions continues sur les treillis, la récursion comme un opérateur de point fixe (solution d’une équation) etc. L’avantage est la certitude d’existence mathématique des objets calculés. L’inconvénient est que ce n’est ni toujours facile, ni toujours très parlant.

Sémantique opérationnelle

On cherche cette fois à décrire l’effet des programmes. On définit un ensemble de valeurs (ou résultats) puis une relation d’évaluation qui relie des programmes avec des résultats.

La principale différence avec la sémantique dénotationnelle est que le domaine sémantique est d’emblée plus simple, on se préoccupe plus de décrire les résultats possibles que de donner un sens mathématique à chaque bout de syntaxe. La définition des programmes comme une relation vient ensuite plus comme une description suffisamment abstraite du calcul que comme la volonté d’associer les programmes à une valeur du domaine. Le formalisme de cette description peut être emprunté à la logique formelle.

3.3  Sémantique opérationnelle de la calculette

3.3.1  Un interpréteur

Une première possibilité est de donner la sémantique opérationnelle comme un programme. Cela revient à écrire un interpréteur. Les valeurs sont les entiers.

On peut définir l’évaluation par un programme Ocaml qui prend un environnement initial associant des valeurs à certaines variables, une expression à évaluer et retourne un entier:

(Notons que la sémantique dénotationnelle donnerait le sens d’un programme comme une fonction des environnements dans les entiers.)

3.3.2  Une présentation plus neutre

Définir la sémantique à l’aide d’un programme interpréteur n’est pas très satisfaisant. La présentation manque à la fois d’abstraction (des détails peu important sont mis en avant) et de neutralité (la description se fait dans un langage de programmation particulier).

On a recours à un formalisme spécifique dit, Sémantique Opérationnelle Structurelle qui, de fait, décrit un interpréteur indépendamment de son implémentation.

L’idée est de définir une relation ρ ⊢ e ⇒ v qui se lit « Dans l’environnement ρ, l’expression e s’évalue en la valeur v », par des règles d’inférence ; c’est-à-dire comme le plus petit ensemble vérifiant une certains nombre de règles d’inférence.

Une règle d’inférence est une implication P₁ ∧ … P_k ⇒ C présentée sous la forme

que l’on peut lire pour réaliser (évaluer) C il faut réaliser à la fois P₁ et … P_k.

Dans les jugements de la forme ρ ⊢ e ⇒ v :

• ρ lie des variables x à des valeurs v, i.e. c’est un par exemple un ensemble de paires notées x ↦ v, mais on peu aussi le définir de façon plus abstraite comme une fonction des noms de variables dans les valeurs.
• Si on prend l’exemple facile de la calculette, on aura e ∈ expressions et v ∈ Z (entiers relatifs). Dans un excès de formalisem, on note ⟨n⟩ l’entier relatif associé à sa représentation n. Les quelques règles suivantes définissent alors la sémantique de la calculette.

  ρ  ⊢   Const n  ⇒   ⟨n⟩

  x ∈ dom(ρ) ρ   ⊢    Variable x   ⇒    ρ(x)

  ρ   ⊢    e1   ⇒    v1           ρ   ⊢    e2   ⇒    v2 ρ   ⊢    Bin (Plus , e1, e2)   ⇒    v1 + v2

  ρ   ⊢    e1   ⇒    v1           ρ   ⊢    e2   ⇒    v2 ρ   ⊢    Bin (Times , e1, e2)   ⇒    v1 * v2

3.4  Diverses constructions et leur sémantique

Sans prétendre a donner formellement toute la sémantique de Pseudo-Pascal. Cette section montre comment exprimer ses constructions (et d’autres) dans le formalisme SOS.

3.4.1  Les liaisons

Commençons par une construction simple : la liaison locale (le let de Caml) de syntaxe concrète :

On ajoute un noeud de syntaxe abstraite :

Informellement, l’expression Let (x, e₁, e₂) lie la variable x à l’expression e₁ dans l’évaluation de l’expression e₂.

Formellement :

où ρ, x ↦ v ajoute la liaison de x à v dans l’environnement ρ en cachant une ancienne liaison éventuelle de x. C’est à dire que ρ, x ↦ v associe v à x, que ρ possède déjà une liaison pour x ou pas.

On voit bien comment on peut comprendre une telle règle en modifiant l’interpréteur des expressions arithmétiques. Les environnements ρ étant codés par des paires l’ajout d’une liaison se code très simplement.

Il reste à étendre la fonction d’évaluation.

Ainsi étant donnée l’expression : let x = 1 in (let x = 2 in x) + x, on a la syntaxe abstraite.

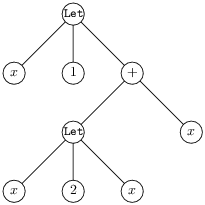
La sémantique est idéalement donnée par un arbre de dérivation qui est la preuve que la valeur de l’expression est 3.

Sous forme compacte, cet arbre exprime aussi un tour d’évaluation de l’interpréteur.

3.4.2  Langages impératifs

Jusqu’ici non avons considéré l’évaluation des expressions. Du point de vue de la sémantique les expressions ont une valeur. Dans notre langage Pseudo-Pascal, comme dans tous les langages impératifs, on considère aussi les instructions. Un ensemble minimal d’instructions comprend l’affectation et la séquence :

Avec pour syntaxe concrète :

Du point de vue sémantique l’exécution d’une instruction ne produit pas de valeur en elle même, mais modifie un « état ». En faisant abstraction des entrées/sorties, on peut limiter l’état à la mémoire. On modélise la mémoire comme une fonction σ des adresses mémoire l dans les valeurs v. L’environnement ρ est maintenant une fonction des noms de variables x dans les adresses l. L’exécution d’une instruction i est rendu par un jugement ρ / σ ⊢ i ⇒ / σ′ qui se lit dans l’état-mémoire σ et l’environnement ρ, l’exécution de l’instruction i produit un nouvel état mémoire σ′. Des règles sémantiques possibles de l’affectation et de la séquence sont alors :

Il faut aussi modifier les règles d’évaluation des expressions pour tenir compte de la mémoire σ. Il n’y a en fait pas grand chose à modifier, sauf peut-être en ce qui concerne l’accès aux variables.

Le traitement impératif des liaisons est bien différent de la liaison let. Les variables peuvent apparaître à gauche du signe d’affectation := et correspondre à des adresses l, ou dans les expressions et correspondre à des valeurs v. On parle alors parfois de left-value et de right-value.

Dans l’évaluateur, on peut se passer d’un encodage explicite de la mémoire en utilisant les valeurs mutables de Caml, c’est à dire que les environnements associent maintenant des noms de variables à des références de Caml.

L’interpréteur est maintenant constitué de deux fonctions, l’une pour évaluer les expressions l’autre pour exécuter les instructions.

Il faut bien remarquer les deux points.

• Nous ne disposons d’aucune règle pour introduire de nouvelles adresses mémoires, c’est à dire pour allouer. Informellement, ce sont les déclarations de variables qui allouent de la mémoire. Par exemple, si on a une déclaration de variable x : integer alors les instructions qui sont dans la portée de cette déclaration, s’exécuteront dans un environnement ρ qui lie x à l’adresse contenant une valeur initiale. En Pseudo-Pascal, cette valeur initiale est une valeur invalide notée ⊥.

  Formellement, mais sans exagérer, imaginons un Pseudo-Pascal très simple qui autorise une seule variable dans les déclarations var. Alors la syntaxe abstraite d’un programme  var x : integer instruction, est un enregistrement :

  type programme = {variable : string ; instruction : instruction}

  L’exécution d’un programme {variable=x ; instruction=i} est rendue par le jugement :

  x ↦ l /  l ↦ ⊥ ⊢  i ⇒   /  σ

  Dans l’interpréteur, on modifie le type des valeurs et on ajoute une fonction chargée d’exécuter les programmes.

  type valeur = Undefined | Int of integer let rec évalue env = function | Const n -> Int n ... and execute env = function ... let execute_programme {variable=x ; instruction=i} = let env = [x, ref Undefined] in execute env i

• Le choix de diviser la syntaxe abstraite entre expressions et instructions est bien un choix. Par exemple, Caml possède bien des traits impératifs, mais pas d’instructions. En ce cas, la séquence et l’affectation doivent rendre un résultat et la règle d’évaluation des expressions doit rendre un état mémoire modifié. Le choix des valeurs rendues est assez simple, la valeur d’une séquence Sequence (e₁, e₂) est la valeur de e₂ et la valeur d’une affectation Affecte (x, e) est la valeur de e. Par exemple, en considérant que la séquence est maintenant une expression, on aura :

  let rec évalue env = function ... | Sequence (e1, e1) -> let _ = évalue env e1 in (* explicitement ignorer v1 *) evalue env e2

3.4.3  Les booléens et la conditionnelle

Les booléens (true et false) nous conduisent à distinguer entre valeurs entières et booléennes. Le domaine des valeurs est alors la réunion de l’ensemble des entiers et de celui des booléens. Si on veut être très formel, il faut alors explicitement utiliser des fonctions canoniques pour passer des entiers aux valeurs et des valeurs aux entiers. On ne le fera pas dans les règles de SOS. Toutefois, il est intéressant de constater que l’implémentation naturelle en Caml du type des valeurs comme un type somme impose d’expliciter ces fonctions canoniques.

En tant que tels les booléens ont peu d’intérêt, il faut se donner une expression conditionnelle pour les utiliser vraiment. La syntaxe en est bien connue :

La sémantique aussi est bien connue.

Soit encore :

On notera que cette construction est particulière, dans le sens que l’evaluation d’une conditionnelle n’entraîne pas systématiquement l’évaluation de ses trois arguments. De fait l’une des expressions e₂ ou e₃ n’est pas évaluée. On parle parfois de construction paresseuse. On notera aussi que pour que les booléens aient un véritable intérêt il faut aussi se donner un certain nombre d’opérateurs supplémentaires par exemple l’inférieur ou égal :

Cela ne pose aucune difficulté si on voit v₁ ≤ v₂ comme une notation traditionnelle pour l’application d’une certaine fonction du produit cartésien des entiers vers les booléens, de même que v₁ + v₂ est la notation traditionnelle d’une certaine fonction du produit cartésien des entiers vers les entiers.

Un point remarquable est le statut de la disjonction et de la conjonction (les « ou » et « et » logique). A priori on a envie de se simplifier la vie en les voyant comme des fonctions bien connues du produit cartésien des booléens vers les booléens. On imagine sans peine les règles associées. Mais, dans la plupart des langages de programmation ils ont une sémantique plus subtile dite paresseuse. Voici par exemple la sémantique du « et ».

La différence entre cette sémantique paresseuse et la sémantique précédente (dite stricte) apparaît quand e₁ vaut faux et que l’evaluation de e₂ déclenche une erreur (voir la section suivante à ce sujet). Avec la sémantique stricte l’evaluation de la conjonction échoue, avec la sémantique paresseuse, l’evaluation rend faux. La sémantique paresseuse est en général préférée précisément à cause de cette propriété : on a plus de programmes corrects pour un prix modique. On notera que la sémantique paresseuse revient à comprendre « e₁  &&  e₂ » comme « if e₁  then  e₂  else  false  ».

Notons que la conditionnelle peut aussi être définie comme une instruction, il n’y a aucune difficulté particulière. On peut alors facilement omettre le else de la conditionnelle.

3.4.4  Formalisation des erreurs

L’évaluation peut mal se passer, même dans la calculette. Par exemple, lors d’une division par 0, de l’accès à une variable non liée, ou de l’evaluation de de la condition d’un if, si le résultat n’est pas un booléen mais un entier. Dans la formalisation de Pseudo-Pascal, l’accès à une variable non initialisée est aussi une erreur.

Si on souhaite formaliser les erreurs, on peut remplacer la relation ρ ⊢ e ⇒ v par une relation ρ ⊢ e ⇒ r où r est une réponse. Les réponses sont l’union des valeurs v ou des erreurs z.

(Il faudrait aussi ajouter d’autres règles pour propager les erreurs, mais c’est assez lourd.)

Le type des erreurs peut être un type somme afin de distinguer les diverses causes d’échec.

Les règles conduisent naturellement à définir les résultats comme un type somme des valeurs et des erreurs

En pratique, on identifie résultats et valeurs et on utilise les exceptions de Caml.

Réciproquement, lorsque l’on s’intéresse surtout à la formalisation des calculs sans erreurs, on peut ne donner que les règles définissant les calculs et considérer que toute erreur se traduit par un arbre bloqué, c’est à dire par que la tentative de preuve du jugement d’évaluation échoue parce qu’une règle spécifique ne peut s’appliquer en raison de la fausseté clairement identifiable de l’une de ses prémisses. Typiquement, pour la division par zéro ce sera la prémisse v₂ ≠ 0.

Dans le cadre de la compilation, il convient d’abord de faire la part des erreurs que le compilateur peut prévenir. Ainsi, le compilateur peut detecter les erreurs de type contenus dans le programme qui lui est proposé et refuser de le compiler, ou dans certains cas (C par exemple) au moins produire un avertissement. Mais toutes les erreurs potentielles ne peuvent pas être détectées par le compilateur. C’est par exemple le cas des divisions par zéro.

Pour comprendre ce qui peut se passer concrètement lors de l’execution d’une erreur vis à vis de la sémantique, supprimons tout contrôle des types préalable et considérons notre interpréteur. Les erreurs peuvent correspondre à des vérifications explicites lors de l’exécution ou pas. Prenons par exemple le cas d’une addition true + 1, notre sémantique interdit cette addition et notre interpréteur échoue en dénonçant une erreur de typage (détectée à l’exécution). Notre interpreteur réagit de cette façon sa représentation des valeurs distingue entiers et booléens. Un autre interpréteur pourrait très bien représenter les booléens à l’aide des entiers (0 pour false et 1 pour true). Un tel interpréteur évalue true + 1 comme 2, résultat qui n’a aucun sens. On notera que le code machine produit par un compilateur se comportera généralement comme ce second interpréteur.

Certaines erreurs risquent fort d’être fatales. Ansi, considérons l’expressiom 1[0] (accès à la première case de 1) et imaginons un compilateur produisant du code machine et démuni de contrôle de type. Lors de l’exécution, le code va tenter de lire le contenu de l’addresse mémoire 1, l’erreur fatale immédiate est assurée, car l’accès à la zone base de la mémoire est généralement interdite.

En conclusion de ces quelques reflexions, retenons que, si la sémantique peut parfois faire l’économie de la formalisation des erreurs, un compilateur ne peut pas les ignorer totalement. Il doit également tenter de les signaler le plus précisément possible, afin de renseigner le programmeur. La combinaison d’un typage statique (le compilateur rejette les programmes mal typés) ou dynamique (le système d’exécution contrôle les types) et de quelques vérifications à l’exécution (principalement les accès dans les tableaux) est à mon avis un minimum.

3.4.5  Terminaison

L’évaluation d’un programme peut ne pas terminer. En sémantique dénotationnelle, le domaine sémantique contient alors une valeur particulière (généralement notée ⊥) qui modélise entre autre cet état de fait. En fait ⊥ est le point minimum des treillis, il représente l’absence d’information. Notons que le formalisme des treillis permet d’exprimer des valeurs partiellement connues. Par exemple la paire (⊥, ⊥) n’est pas forcément ⊥, on sait au moins que c’est une paire, alors qu’avec ⊥, on ne sait rien du tout.

En SOS à grands pas, c’est à dire en SOS telle que nous l’avons vue jusqu’ici, on ne peut pas modéliser la non-terminaison. En effet, ce formalisme ne sait parler que des programmes qui terminent. On identifie alors tous les programmes qui ne terminent pas, en quelque sorte par défaut. Pourtant, et c’est particulièrement vrai des programmes impératifs, des programmes peuvent ne pas terminer et ne pas faire tous la même chose, on peut donc souhaiter les distinguer dans la sémantique.

Une façon de procéder est de définir une SOS dite « à petits pas ». Le calcul est modélisé par une relation de réduction interne, ie. les programmes se réduisent sur eux mêmes (chaque étape élémentaire du calcul est modélisée par un petit pas de réduction) jusqu’à obtention d’une valeur éventuelle. (Voir le cours Sémantique des langages de programmation).

3.4.6  Ordre d’évaluation

Le formalisme SOS semble ne pas spécifier l’ordre d’évaluation des arguments disons d’une addition :

Cette écriture nous dit que pour calculer v, il faut calculer v₁ et v₂, elle ne dit pas qu’il faut calculer v₁ avant v₂ ou le contraire.

En revanche, la règle de la liaison dit bien dans quel ordre calculer, en raison de la dépendance explicite sur v₁.

De même, dans la formalisation impérative, l’ordre d’exécution des instructions est toujours fixé, en raison des dépendances dues à la mémoire σ. Il en sera de même si la mémoire apparaît dans les règles d’évaluation des expressions. Dans ce cas, l’ordre choisi est le plus souvent de la gauche vers la droite.

Dans les cas les plus simples comme celui de la calculette, l’ordre d’évaluation n’est de toute façon pas observable, le résultat est le même quelque soit l’ordre d’évaluation. Ce n’est plus le cas lorsque le langage est suffisamment expressif pour que l’on puisse écrire des programmes qui ne terminent pas et que des erreurs peuvent se produire. Par exemple en Caml :

Si les arguments de l’addition sont évalués de la gauche vers la droite, alors le programme ci-dessus échoue à cause de la division par zéro, dans le cas droite-gauche, le programme ne termine pas.

Remarquons que, en cas de formalisation des erreurs, la sémantique SOS tend à spécifier l’ordre d’évaluation de façon un peu implicite. Ainsi la règle de la division par zéro peut s’exprimer de deux façons :

L’évaluation est de droite à gauche dans le premier choix et de gauche à droite dans le second. Notons tout de même que la SOS est censée définir une relation entre expressions et résultats et non pas une fonction. Dès lors, on pourrait théoriquement associer plusieurs résultats à un programme donné, par exemple en se donnant les deux règles de la division. Mais ça ne se fait pas trop…

En dernière analyse, l’implémentation d’un langage devra bien évaluer les expressions dans un certain ordre. On peut peut-être considérer que ça n’a pas trop d’importance dans le cas des erreurs et de la non-terminaison, mais, en pratique, l’effet de l’ordre d’évaluation des expressions est notable lorsque l’on procède à des effets de bord dans les expressions. Se pose alors la question de savoir si cet ordre est fixé par la sémantique (même informelle) ou laissé à l’appréciation de l’implémenteur. La tendance actuelle est de spécifier l’ordre d’évaluation dans la sémantique (cf. Java), l’avantage est que toutes les implémentations conformes à la sémantique traitent tous les programmes de la même façon. L’avantage de ne pas spécifier l’ordre est que l’implémenteur peut profiter de la liberté qui lui est donnée pour introduire des optimisations (cf. C et Caml). Dans ce cadre l’ordre d’évaluation n’est bien spécifié que pour un certain nombre de constructions (typiquement la séquence, la liaison let).

Mon avis sur la question

De toute façon, les programmes qui terminent, sont exempts d’erreurs et bien écrits (de mon point de vue) ne sont pas concernés. Utiliser l’ordre d’évaluation des arguments par exemple de l’addition n’est certainement pas de la bonne programmation, car le programme fonctionne alors un peu par miracle. Chaque fois que cet ordre est important il vaut mieux l’exprimer clairement en décomposant à l’aide de la séquence ou du let. Pour lire un entier décimal sous forme de deux caractères pris dans l’entrée standard, on évitera d’écrire :

On écrira plutôt :

Ainsi il apparaît clairement que le chiffre des dizaines vient avant celui des unités, et je recommande ce style y compris en Java où la première écriture est correcte.

Enfin, une conséquence un peu surprenante de l’indétermination de l’ordre d’évaluation en Caml est qu’il est possible de laisser l’ordre d’évaluation non spécifié dans l’interpréteur. Par exemple, on avait écrit :

Comme, dans l’expression let d₁ and d₂ in e, rien n’est sûr sur l’ordre d’évaluation respectif de d₁ et de d₂, le programme interpréteur ne dit rien sur l’ordre de calcul respectif de v₁ et de v₂.

3.4.7  Tableaux

Nous étudions ici les tableaux impératifs, c’est à dire munis d’une instruction d’affectation. Nous supposerons pour simplifier que les tableaux sont alloués dynamiquement et explicitement (leur durée de vie est infinie).

On ajoute trois constructions à la syntaxe :

• L’expression Alloc (e₁) alloue un nouveau tableau de taille la valeur de e₁ les cases du nouveau tableau sont indéfinies
• L’expression Lire (e₁, e₂) lit la case (correspondant à la valeur de) e₂ du tableau (la valeur de) e₁.
• L’instruction Ecrire (e₁, e₂, e₃) écrit la case e₂ du tableau e₁ avec la valeur de e₃.

Soit encore :

Avec pour syntaxe concrète :

On peut modéliser les tableaux en tant que valeurs tout simplement par des adresses. On doit alors se donner un minimum d’arithmétique sur les adresses (l’adresse de la case i du tableau t est l’adresse t+i). C’est bien ainsi que les tableaux sont implémentés dans les langages comme C ou Pascal. Pour la sémantique, voyons donc plutôt un tableau t comme une fonction d’un intervalle entier dans les adresses, que l’on note comme les environnements. On se donne aussi une valeur invalide notée ⊥. À cause du parti-pris un peu arbitraire de ne pas modifier la mémoire dans l’évaluation des expressions, l’allocation ne peut apparaître disons que lors d’une affectation :

Création

Lecture

Écriture

Notons que les règles exhibent de nombreuses conditions explicites, outre la contrainte de fraîcheur des adresses ( l₀ ∉dom(σ), etc.) qui est idéalement toujours satisfaite, on remarque des conditions de bon typage (les indices sont des entiers) et des conditions liées aux bornes des tableaux ( k ≥ 0 et k ∈ dom(t)) que le typage ne détecte pas en général.

Pour l’interpréteur, on profite des tableaux mutables du langage hôte.

En raison de la représentation des valeurs, l’interpréteur signalera nécessairement les erreurs de type.

En outre, parce que les accès en dehors des bornes d’un tableau sont détectés par Caml, l’interpréteur signale nécessairement ce type d’erreur. Le code suivant procède toutefois à une vérification explicite, afin de maîtriser le signalement des erreurs (sinon on aurait des exceptions Invalid_Argument of string).

On notera que comme Caml vérifie les accès aux tableau (et lève l’exception Invalid_Argument of string en cas d’accès hors-bornes), on aurait pu se passer de test explicite sur les indices.

3.5  Les fonctions

3.5.1  Les fonctions globales

Dans un langage comme C (ou Pseudo-Pascal) les fonctions ne peuvent être définies qu’au niveau « supérieur » (top-level), c’est à dire globalement. Un programme complet est tout simplement une suite de de définitions de fonctions. Ensuite en C il existe une fonction de nom conventionnel (main) et l’execution du programme est un appel de cette fonction. Tandis qu’en Pseudo-Pascal le programme comprend aussi en plus de la suite de définitions une instruction à exécuter.

Soyons plus précis en considérant une calculette fonctionnelle. Le programme est tout simplement une liste de définitions de fonctions à un argument, plus une expression à évaluer. Une fonction de nom f est donc une association f ↦ (x,e) , où x est le nom du paramètre de la fonction et e est son corps.

La syntaxe abstraite des expressions est étendue par une construction d’application :

Ainsi sans rentrer exagérément dans les détails, le calcul de 10! avec une telle calculette pourrait s’écrire :

Pour tenir compte des définitions de fonctions dans la sémantique on peut considérer l’évaluation par rapport à deux environnements ρ_f pour les fonctions et ρ pour les valeurs ordinaires. La sémantique de l’application est alors :

La définition informelle serait que l’évaluation de l’application d’une fonction est l’evaluation de son corps dans un environnement limité à la liaison de son paramètre à la valeur de l’argument.

L’écriture de l’interpréteur serait alors :

L’environnement ρ_f ne change jamais au cours de l’évaluation, il est en quelque sorte global. Il est conceptuellement simple d’imaginer qu’il contient, en plus des fonctions, toutes les liaisons globales d’un programme. Pour ce qui est de la compilation, on notera qu’un programme ne comporte qu’un nombre fini de fonctions et de variables globales bien connues, et que donc le compilateur peut allouer statiquement l’espace à eux nécessaire. Par contraste, les autres liaisons (celles des arguments et des variables locales) sont réalisées en pile, l’espace nécessaire est réservé au moment de l’appel des fonctions et rendu au moment de leur retour. Cela est correct, car on peut plus accéder aux valeurs des arguments et des variables locales d’une fonction une fois que cette fonction a retourné.

Il est important de remarquer que les fonctions telles que décrites ci-dessus sont assez limitées. À part des noms de fonctions (ou des variables globales), la seule variable qui peut apparaître dans le corps de la fonction est le paramètre. Bien sûr, en pratique, il peut y avoir plusieurs paramètres et la fonction peut également déclarer des variables locales. On obtient ainsi par exemple les fonctions du langage C.

En Caml les fonctions sont plus puissantes dans le sens que d’autres variables peuvent apparaître dans le corps de fonction :

Dans le code ci-dessus, la variable y apparaît dans le corps de la fonction g, bien que ce ne soit pas un paramètre de g. Dans le même ordre d’idée, en Java, les champs d’un objet peuvent apparaître dans le corps des méthodes.

3.5.2  Appel par valeur

L’appel des fonctions de la section précédente est par valeur. C’est à dire que l’appel de fonction crée une nouvelle liaison entre le nom de l’argument (paramètre formel) et la valeur de l’argument (paramètre effectif). Il est intéressant de modéliser le même comportement dans le cas impératif (section 3.4.2), en présence d’une construction d’affectation. Une variable est maintenant réalisée par une double liaison, des noms aux adresses, puis des adresses aux valeurs (ρ et σ). La règle de l’appel par valeur réclame l’allocation d’une nouvelle case mémoire d’adresse l_a pour y ranger la valeur de l’argument.

Cette écriture explicite la création d’une nouvelle adresse l_a. On peut aussi voir que la nouvelle adresse l_a n’est accessible que lors de l’évaluation du corps e_f. Cela suggère fortement la réalisation de la liaison entre paramètre formel et paramètre effectif à l’aide d’une pile.

Mais pourquoi alors ne pas créer simplement une nouvelle liaison de variable à adresse, sans créer de nouvelle liaison d’adresse à valeur ? Cela n’a une signification simple que le paramètre effectif possède clairement une adresse, c’est à dire que lorsque le paramètre effectif est une variable. On pourrait alors écrire cette règle :

En Pascal, on spécifie qu’un paramètre est passé par variable en utilisant le mot-clé var lors de la définition des fonctions. Par défaut le passage est par valeur. Soient par exemple les deux programmes complets suivant.

Le premier programme affiche 1 tandis que le second affiche 2. L’appel par variable fait que x et y sont deux synonymes de la même case mémoire, on parle alors d’alias.

Les paramètres tableaux

Dans le cadre de Pseudo-Pascal, la règle de l’appel de fonction est la règle d’appel par valeur des langages impératifs donnée au début de cette section, que nous rappelons :

Si v_a est un tableau t = (0↦ l₀, …, k−1↦ l_k−1) alors une nouvelle liaison de x à l_a puis à t est créée, comme dans le cas général. Le point important est que les adresses l₀, …, l_k−1 ne changent pas, ainsi une modification du tableau à l’intérieur de la fonction sera visible après le retour de celle-ci. En revanche, une affectation de la variable x reste toujours invisible de l’extérieur. Le tableau est bien passé par valeur, mais c’est sémantiquement une référence (nom abstrait des adresses) vers une structure mutable (une zone de mémoire où on peut écrire). On peut faire le lien avec Java par exemple, où les objets sont des références, mais aussi avec C, où les tableaux sont expressément définis comme (presque) équivalents à l’adresse en mémoire de leur première case.

Pascal procède différemment. Si une fonction prend un paramètre tableau, alors le paramètre formel sera lié à une copie du tableau effectif. C’est à dire que sémantiquement les tableaux ne sont plus des références vers des zones mémoire, mais bien des zones mémoire elles-mêmes. En outre, si le mot-clé var précède la définition du paramètre formel, celui ci sera en fait une référence vers la zone mémoire du tableau effectif et les modifications des cases du tableau porteront sur les cases du tableau effectif.

3.5.3  Culture : Fonctions de première classe

Si l’on souhaite que les fonctions soient valeurs du langage au même titre que les entiers, on va se retrouver confronté à un problème sémantique. L’origine de ce problème réside dans les variables dites libres des fonctions c’est à dire dans les variables qui apparaissent dans le corps des fonctions et qui ne sont ni des arguments, ni des variables locales. Considérons cet exemple de Caml :

La variable x est libre dans la définition de mem et possède deux définitions. Doit-on lorsque l’on évalue le corps de mem choisir la liaison de x à 1 ou celle de  x à 2 ? Si l’on fait le choix de la liaison valide au moment de la définition de la fonction mem, alors on parle de liaison lexicale (C, Pascal, Caml). Si on fait le choix de de la liaison valide au moment de l’appel de la fonction mem, alors on parle de liaison dynamique (vieux Lisp, Basic).

La liaison lexicale est préférée parce qu’elle permet de toujours de connaître la déclaration d’une variable libre sans appeler la fonction, c’est à dire qu’un compilateur sait toujours ou aller chercher sa valeur en mémoire, quel est son type etc. Mais aussi, un programmeur sait toujours de quelle « variable » il s’agit et la robustesse des programmes s’en trouve augmentée.

Notons que si notre langage de programmation permet de rendre des fonctions comme des résultats de fonctions, la liaison lexicale est obligatoire, voici par exemple la définition de la composition de fonction en Caml :

On ne voit pas très bien ce que pourrait signifier la liaison dynamique dans ce cas. En revanche, le sens de la liaison lexicale est clair : au moment de la définition de la fonction h, les valeurs de f et g (libres dans la définition de h) sont bien connues. Un appel ultérieur à h doit savoir les retrouver.

La solution la plus simple et la plus générale pour implémenter les fonctions de première classe est la fermeture. Une fermeture est une paire d’un environnement et du corps de cette fonction, l’environnement sera pris comme étant celui qui est valide au moment de la définition de la fonction.

Construisons donc une calculette authentiquement fonctionnelle, à partir de ce principe. Le plus simple est de considérer des fonctions anonymes et une construction d’application plus générale que précédemment :

Les valeurs doivent maintenant comprendre les fermetures. En SOS, on peut les noter ⟨x, ρ, e⟩ (x est le paramètre), et pour les valeurs de l’interpréteur on peut écrire :

Les règles de création de fermeture et d’application sont alors :

Et le code de l’interpréteur est :

On notera le grand intérêt de l’idée de la fermeture. L’expressivité du langage est considérablement augmentée par rapport aux fonctions globales et la sémantique n’est pas vraiment plus compliquée.

On peut se demander alors pourquoi tous les langages n’offrent pas les fonctions de première classe. Je crois que la réponse tient principalement à des questions d’implémentation. Dans le cadre de la compilation, le seul problème de cette approche des fonctions par les fermetures est que les liaisons des variables ne peuvent plus, en toute généralité, être réalisées statiquement ou en pile. En effet, dans l’exemple de la fonction compose les liaisons de f et g survivent à l’appel de compose puisqu’elles existent encore lors de l’appel ultérieur de h. Le code du corps de la fonction h ne pourra donc pas aller chercher les valeurs de f et g dans la pile là où elles se trouvaient normalement au moment de la création de h (ce sont des arguments de compose) Il faut donc allouer les environnements dynamiquement et cette allocation est implicite, ce qui à son tour impose de disposer d’un glaneur de cellules (garbage collector) chargé de récupérer automatiquement la mémoire qui n’est plus utilisée.

On peut toutefois faire les deux remarques suivantes :

• L’environnement des fermetures n’a pas besoin de contenir des liaisons pour tout le domaine valide au moment de la création de la fermeture, contrairement à ce que semble affirmer notre sémantique. On peut se contenter des seules variables effectivement libres dans la fonction créée. L’avantage est que les environnements des fermetures seront plus petits et que la mémoire est plus efficacement gérée.
• Si il est interdit de rendre les fonctions comme résultat, alors l’environnement peut être réalisé en pile uniquement. Pascal procède de cette façon : les fonctions peuvent être définies dans d’autres fonctions (et alors les liaisons des variables libres ne peuvent pas toutes être allouées statiquement par le compilateur), et passées comme arguments. La description exacte des techniques d’implémentation nécessaires dépasse un peu le cadre du cours, mais on comprendra que dans le cadre de cette restriction, toutes les valeurs des variables libres se trouvent bien quelque part dans la pile, dans la portion de pile allouée lors de l’appel des fonctions qui les définissent, appels qui tous n’ont pas encore retourné.

  Une implémentation possible de ce type de fonctions consiste à supprimer les variables libres en les remplaçant par des arguments supplémentaires (attention, ce n’est pas ainsi que Pascal procède traditionnellement). Ainsi les deux programmes suivants (en syntaxe Caml) font la même chose.

  La variable x est libre dans mem. let member (x,l) = let rec mem l = match l with | [] -> false | h::t -> x = h || mem t in mem l

  La variable x est un argument de mem. let member (x,l) = let rec mem (x,l) = match l with | [] -> false | h::t -> x = h || mem (x,t) in mem (x,l)

  On notera que la transformation du programme de gauche en celui de droite n’est possible que parce que tous les appels de mem sont connus.

3.6  Le langage Pseudo-Pascal (PP)

C’est un Pascal simplifié et subtilement modifié en ce qui concerne les tableaux.

3.6.1  Syntaxe

La syntaxe concrète est (presque) celle de Pascal.

La syntaxe abstraite est définie en Caml. On conserve les informations de types (pour permettre une analyse de type ultérieure)

Un programme est composé d’un ensemble de déclarations de variables, de fonctions et d’un corps (une instruction).

Les expressions

Les instructions

3.6.2  Sémantique

• Le langage est impératif et distingue les expressions et les instructions. Les constructions des instructions sont classiques (affectation, séquence, conditionnelle, boucle while), plus deux « primitives » pour écrire et lire un entier (read_int et write_int).
• Les valeurs sont les entiers, les booléens et les tableaux. Sémantiquement les tableaux sont des références. Les tableaux sont alloués dynamiquement (durée de vie infinie).
• L’ordre d’évaluation est de gauche à droite.
• Les fonctions sont globales, mutuellement récursives et ne peuvent qu’être appelées. Les fonctions se divisent en procédures qui ne rendent pas de résultat, et en fonctions proprement dites. L’appel de procédure est une instruction, tandis que l’appel de fonction est une expression. Notons que les corps des fonctions sont en fait une instruction et que, selon la convention de Pascal, le résultat d’une fonction est passé en affectant la variable homonyme (pas d’instruction return). Attention, toutes les règles vues pour les fonctions considéraient que le corps d’une fonction est une expression…
• Les arguments des fonctions sont passés par valeur.
• Les retours de fonction et les affectations suivent la même convention.
• Les variables sont toutes mutables (y compris celles de type tableau) et la portée est lexicale.
• Les variables sont déclarées (leur type est spécifié à ce moment), comme variables globales, variables locales ou arguments. La portée et la durée de vie est infinie pour les premières, limitée à un appel pour les autres.

C’est à vous d’écrire un interpréteur, en grapillant dans ce cours et en utilisant votre culture.