| Figure 2.1: Une pile (ajouter et retirer du même côté), une file (ajouter et retirer de côtés opposés). |




Les piles et les files sont des exemples de structures de données que faute de mieux, nous appellerons des sacs. Un sac offre trois opérations élémentaires :
Le sac est une structure impérative : un sac se modifie au cours du
temps. En Java, il est logique de représenter un sac (d’éléments E)
par un objet (d’une classe Bag⟨E⟩) qui possède
trois méthodes.
Ainsi on ajoute par exemple un élément e dans le sac b par b.add(e), ce qui modifie l’état interne du sac.
Piles et files se distinguent par la relation entre éléments ajoutés et éléments retirés. Dans le cas des piles, c’est le dernier élément ajouté qui est retiré. Dans le cas d’une file c’est le premier élément ajouté qui est retiré. On dit que la pile est une structure LIFO (last-in first-out), et que la file est une structure FIFO (first-in first-out).
Si on représente pile et file par des tas de cases, on voit que la pile possède un sommet, où sont ajoutés et d’où sont retirés les éléments, tandis que la file possède une entrée et une sortie.
Figure 2.1: Une pile (ajouter et retirer du même côté), une file (ajouter et retirer de côtés opposés). 
Tout ceci est parfaitement conforme à l’intuition d’une pile d’assiettes, ou de la queue devant un guichet, et suggère fortement des techniques d’implémentations pour les piles et les files.
Il y a un peu de vocabulaire spécifique aux piles et aux files. Traditionnellement, ajouter un élément dans une pile se dit empiler (push), et l’enlever dépiler (pop), tandis qu’ajouter un élément dans une file se dit enfiler, et l’enlever défiler.
La file est peut-être la structure la plus immédiate, elle modélise directement les files d’attente gérées selon la politique premier-arrivé, premier-servi. La pile est plus informatique par nature. Dans la vie, la politique dernier-arrivé, premier-servi n’est pas très populaire. Elle correspond pourtant à une situation courante, la survenue de tâches de plus en plus urgentes. Les piles modélisent aussi tout système où l’entrée et la sortie se font par le même passage obligé : wagons sur une voie de garage, cabine de téléphérique, etc.
Utiliser une file informatique est donc naturel lorsque l’on modélise une file d’attente au sens courant du terme. Considérons un exemple simple :
Notre objectif est d’écrire une simulation informatique afin d’estimer le rapport clients repartis sans être servis sur nombre total de clients, en fonction de la probabilité p.
Nous implémentons la simulation par une classe
Simul (source Simul.java).
Pour réaliser les tirages aléatoires nécessaires,
nous employons une source pseudo-aléatoire, les objets de la classe
Random du package java.util
(voir B.1.4 pour la notion de package
et B.6.3.1 pour une description de Random).
Un client en attente est modélisé par un objet de la
classe Client. Un objet Client est créé lors de l’arrivée du
client au temps t, ce qui donne l’occasion de calculer l’heure à
laquelle le client exaspéré repartira s’il il n’a pas été servi.
Noter que les constantes qui gouvernent le temps d’attente sont
des variables final de la classe Client.
L’implémentation d’une file sera décrite plus tard.
Pour l’instant une file (de clients) est un objet de la classe
Fifo qui possède les méthodes isEmpty, add et
remove décrites pour les Bag de l’introduction.
La simulation est discrète. Durant la simulation, une variable tFree indique la date où le guichet sera libre. À chaque seconde t, il faut :
Le code qui réalise cette simulation naïve en donné par la
figure 2.2.
La méthode simul prend la probabilité d’arrivée d’un client en
argument et
renvoie le rapport clients non-servis sur nombre total de clients.
static double simul(double probNewClient) {
Fifo f = new Fifo () ;
int nbClients = 0, nbFedUp = 0 ;
int tFree = 0 ; // Le guichet est libre au temps tFree
for (int t = 0 ; t < tMax ; t++) {
// Tirer l'arrivée d'un client dans [t..t+1[
if (occurs(probNewClient)) {
nbClients++ ;
f.add(new Client(t)) ;
}
if (tFree <= t) {
// Le guichet est libre, servir un client (si il y en a encore un)
while (!f.isEmpty()) {
Client c = f.remove() ;
if (c.departure >= t) { // Le client est encore là
tFree = t + uniform(serviceMin, serviceMax) ;
break ; // Sortir de la boucle while
} else { // Le client était parti
nbFedUp++ ;
}
}
}
}
return ((double)nbFedUp)/nbClients ;
}
Le code suit les grandes lignes de la description précédente.
Il faut surtout noter comment on résout le problème d’une
boucle while qui doit d’une part s’effectuer tant que la file
n’est pas vide et d’autre part cesser dès qu’un client effectivement
présent est extrait de la file (sortie par break).
On note aussi la conversion de type explicite
((double)nbFedUp)/nbClients, nécessaire pour forcer la division
flottante. Sans cette conversion on aurait la division euclidienne.
La figure 2.3 donne les résultats de la simulation pour
diverses valeurs de la probabilité prob. Il s’agit de moyennes sur
dix essais.
Nous allons prendre en compte la nature très informatique de la pile et proposer un exemple plutôt informatique. Les calculatrices d’une célèbre marque états-unienne ont popularisé une notation des calculs dite parfois « polonaise inverse »1 ou plus généralement postfixe. Les calculs se font à l’aide d’une pile, les nombres sont simplement empilés, et l’exécution d’une opération op revient à d’abord dépiler un premier opérateur e1, puis un second e2, et enfin à empiler le résultat e2 op e1. Par exemple, la figure 2.4 donne les étapes successives du calcul 6 3 2 - 1 + / 9 6 - * exprimé en notation postfixe.
Le fabricant états-unien de calculatrices
affirme
qu’avec un peu
d’habitude la notation postfixe est plus commode que la notation usuelle
(dite infixe).
C’est peut-être vrai, mais on peut en tout cas être sûr que l’interprétation
de la notation postfixe par une machine est bien plus facile à
réaliser que celle de la notation infixe.
En voici pour preuve le
programme Calc (source Calc.java)
qui réalise
le calcul postfixe donné sur la ligne de commande.
Dans ce code les objets de la classe Stack sont des piles
d’entiers.
Le source contient des messages de diagnostic (sur System.err on
n’insistera jamais assez),
un essai2
nous donne (le sommet de pile est à droite) :
% java Calc 6 3 2 - 1 + / 9 6 - ’*’ 6 -> [6] 3 -> [6, 3] ⋮ 6 -> [3, 9, 6] - -> [3, 3] * -> [9] 9
La facilité d’interprétation de l’expression postfixe provient de ce que sa définition est très opérationnelle, elle dit exactement quoi faire. Dans le cas de la notation infixe, il faut régler le problème des priorités des opérateurs. Par exemple si on veut effectuer le calcul infixe 1 + 2 * 3 il faut procéder à la multiplication d’abord (seconde opération), puis à l’addition (première opération) ; tandis que pour calculer 1 * 2 + 3, on effectue d’abord la première opération (multiplication) puis la seconde (addition). Par contraste, la notation postfixe oblige l’utilisateur de la calculatrice à donner l’ordre désiré des opérations (comme par exemple 1 2 3 * + et 1 2 * 3 +) et donc simplifie d’autant le travail de la calculatrice. Dans le même ordre d’idée, la notation postfixe rend les parenthèses inutiles (ou empêche de les utiliser selon le point de vue).
Infix qui lit une expression sous forme
postfixe et affiche l’expression infixe (complètement parenthésée)
qui correspond au calcul effectué par le programme Calc.
On supposera donnée une classe Stack des piles de chaînes.
% java Infix 6 3 2 - 1 + / 9 6 - ’*’ 6 -> [6] 3 -> [6, 3] ⋮ 6 -> [(6/((3-2)+1)), 9, 6] - -> [(6/((3-2)+1)), (9-6)] * -> [((6/((3-2)+1))*(9-6))] ((6/((3-2)+1))*(9-6))Nous verrons plus tard que se passer des parenthèses inutiles ne se fait simplement qu’à l’aide d’une nouvelle notion. □
Nous donnons d’abord deux techniques d’implémentation possibles, avec un tableau et avec une liste simplement chaînée. Ensuite, nous montrons comment utiliser la structure de pile toute faite de la bibliothèque.
C’est la technique conceptuellement la plus simple, directement inspirée par le dessin de gauche de la figure 2.1.
Plus précisément, une pile (d’entiers) contient un tableau d’entiers, dont nous fixons la taille arbitrairement à une valeur constante. Seul le début du tableau (un segment initial) est utilisé, et un indice variable sp indique le pointeur de la pile. Le pointeur de pile indique la prochaine position libre dans la pile, mais aussi le nombre d’éléments présents dans la pile.

Dans ce schéma, seules les 5 premières valeurs du tableau sont significatives.
Notons que tous les champs des objets Stack sont privés
(private, voir B.1.4).
La taille des piles est donnée par une constante
(final), statique puisque qu’il n’y a aucune raison
de créer de nombreux exemplaires de cette constante.
À la création, une pile contient donc un tableau de SIZE=10 entiers. La valeur initiale contenue dans les cases du tableau est zéro (voir B.3.6.2), mais cela n’a pas d’importance ici, car aucune case n’est valide (sp est nul).

Il nous reste à coder les trois méthodes des objets de la
classe Stack pour respectivement,
tester si la pile est vide, empiler et dépiler.
La figure 2.5 donne un exemple d’évolution du tableau t et du pointeur de pile sp.
Figure 2.5: Empiler 9, puis dépiler. 
Le code ci-dessus signale les erreurs en lançant l’exception Error (voir B.4.2), et emploie les opérateurs de post-incrément et pré-décrément (voir B.3.4). Notons surtout que toutes opérations sont en temps constant, indépendant du nombre d’éléments contenus dans la pile, ce qui semble attendu dans le cas d’opérations aussi simples que push et pop.
Les deux erreurs possibles "Push : pile pleine"
et "Pop : pile vide" sont de natures bien différentes.
En effet, la première découle d’une contrainte technique
(la pile est insuffisamment dimensionnée), tandis que la seconde
découle d’une erreur de programmation de l’utilisateur de la pile.
Nous allons voir ce que nous pouvons faire au sujet de ces deux
erreurs.
Commençons par l’erreur "pile pleine".
Une première technique simple est de passer le bébé à l’utilisateur,
en lui permettant de dimensionner la pile lui-même.
Ainsi, en cas de pile pleine, on peut toujours compter sur l’utilisateur pour recommencer avec une pile plus grande. Cela paraît abusif, mais c’est à peu près ce qui se passe au sujet de la pile des appels de méthode.
Mais en fait, les tableaux de Java sont suffisamment flexibles pour autoriser le redimensionnement automatique de la pile. Il suffit d’allouer un nouveau tableau plus grand, de recopier les éléments de l’ancien tableau dans le nouveau, puis de remplacer l’ancien tableau par le nouveau (et dans cet ordre, c’est plus simple).
Le redimensionnement automatique offre une flexibilité maximale. En contrepartie, il a un coût : un appel à push ne s’exécute plus en temps garanti constant, puisqu’il peut arriver qu’un appel à push entraîne un redimensionnement dont le coût est manifestement proportionnel à la taille de la pile.
Mais vu globalement sur une exécution complète, le coût de N appels
à push reste de l’ordre de N. On dira alors que le coût
amorti de push est constant. En effet, considérons
N opérations push. Au pire, il n’y a pas de pop et la pile
contient finalement N éléments pour une taille 2P du tableau
interne, où 2P est la plus petite puissance de 2 supérieure à N.
En outre, supposons que le tableau est
redimensionné P fois (taille initiale 20). L’ordre de grandeur
du coût cumulé de tous les push est donc de l’ordre de N (coût
constant de N push) plus ∑k=1k=P 2k = 2P+1−1
(coût des P redimensionnements). Soit un coût final de l’ordre de
N, puisque 2P < 2·N. Pour ce qui est de la mémoire, on
alloue au total de l’ordre de 2P+1 cellules de mémoire, dont la
moitié ont pu être récupérées par le garbage collector.
Notons finalement que le coût amorti constant est assuré quand
les tailles des tableaux successifs suivent une progression
géométrique, dont la raison n’est pas forcément 2.
En revanche, le coût amorti devient linéaire pour des tableaux
les tailles suivent une progression arithmétique.
Pour cette raison, écrire int [] newT = new int [t.length + K]
est rarement une bonne idée.
Abordons maintenant l’erreur "pile vide".
Ici, il n’y a aucun moyen de supprimer l’erreur, car rien n’empêchera
jamais un programmeur maladroit ou fatigué de dépiler une pile vide.
Mais on peut signaler l’erreur plus proprement, ce qui donne la
possibilité au programmeur fautif de la réparer.
Pour ce faire, il convient de lancer, non plus l’exception
Error, mais une exception spécifique.
Les exceptions sont complètement décrites dans l’annexe Java
en B.4.
Ici, nous nous contentons d’une présentation minimale.
La nouvelle exception StackEmpty se définit
ainsi.
C’est en fait une déclaration de classe ordinaire, car une exception est un objet d’une classe un peu spéciale (voir B.4.2). La nouvelle exception se lance ainsi.
On note surtout que la méthode pop déclare (par throws, noter
le « s ») qu’elle peut lancer l’exception StackEmpty. Cette
déclaration est ici obligatoire, parce que StackEmpty
est une Exception et non plus une Error.
La présence de la déclaration va obliger l’utilisateur des
piles à s’occuper de l’erreur possible.
Pour illustrer ce point revenons sur l’exemple de la
calculatrice Calc (voir 2.1.2).
La calculatrice emploie une pile stack, elle dépile et empile
directement par stack.pop() et stack.push(…).
Nous supposons que la classe Stack est telle que ci-dessus
(avec une méthode pop qui déclare lancer StackEmpty)
et que nous ne pouvons pas modifier son code.
Pour organiser un peu la suite, nous ajoutons deux nouvelles méthodes
statiques push et pop à la classe Calc, et transformons les
appels de méthode dynamiques en appels statiques.
Le compilateur refuse le programme ainsi modifié.
Il exige le traitement de StackEmpty
qui peut être lancée par stack.pop().
Traiter l’exception peut se faire en attrapant
l’exception, par l’instruction try.
L’effet est ici que si l’instruction return stack.pop() échoue
parce que l’exception StackEmpty est lancée, c’est alors
l’instruction return 0 qui s’exécute.
Cela revient à remplacer la valeur « exceptionnelle »
StackEmpty par la valeur plus normale 0
(voir B.4.1 pour les détails).
Par conséquent, une pile vide se comporte comme si elle contenait
une infinité de zéros.
On peut aussi décider de ne pas traiter l’exception, mais alors
il faut signaler que les méthodes Calc.pop puis main
peuvent lancer l’exception StackEmpty, même si c’est indirectement.
Si l’exception survient, elle remontera de méthode en méthode et fera
finalement échouer le programme.
En fait, comme les déclarations throws, ici obligatoires,
sont quand même pénibles, on a plutôt tendance à faire échouer le
programme explicitement dès que l’exception atteint le code
que l’on contrôle.
Bien sûr, si on veut que dépiler une pile vide provoque un arrêt du
programme, il aurait été plus court de lancer
new Error ("Pop : pile vide") dans la méthode pop
des objets Stack. Mais nous
nous sommes interdit de modifier la classe Stack.
C’est particulièrement simple. En effet, les éléments sont empilés et dépilés du même côte de la pile, qui peut être le début d’une liste. On suppose donc donnée une classe des listes (d’entiers). Et on écrit :
Voici un exemple d’évolution de la liste p.

Il existe déjà une classe des piles dans la bibliothèque, la classe Stack du package java.util, implémentée selon la technique des tableaux redimensionnés. Mais une classe des piles de quoi ?
En effet, dans les deux sections précédentes, nous n’avons codé que
des piles de int en nous disant que pour coder une pile, par
exemple de String, il nous suffisait de remplacer int
par String partout dans le code. Il est clair qu’une telle
« solution » ne convient pas à une classe de bibliothèque qui est
compilée par le fabricant. Après bien des hésitations, Java a résolu
ce problème en proposant des classes génériques, ou
paramétrées. La classe Stack est en fait une classe
Stack<E>, où
E est n’importe quelle classe,
et les objets de la classe Stack<E> sont des piles
d’objets de la classe E.
Formellement, Stack n’est donc pas exactement une classe, mais
plutôt une fonction des classes dans les classes.
Informellement, on peut considérer que nous disposons d’une
infinité de classes Stack<String>, Stack<List> etc.
Par exemple on code facilement la pile de chaînes de
l’exercice 2.2 comme un objet de la
classe java.util.Stack<String> (source Infix.java).
(Pour import, voir B.3.5.)
Cela fonctionne parce que la classe Stack<E>
possède bien des méthodes pop et push, où par
exemple pop() renvoie un objet E, ici un String.
Comme le paramètre E dans Stack<E>
est une classe, il n’est pas
possible de fabriquer des piles de int.
Plus généralement, il est impossible de fabriquer des piles de
scalaires (voir B.3.1 pour la définition des scalaires).
Mais la bibliothèque fournit une classe associée par type
scalaire, par exemple Integer pour int.
Un objet Integer n’est guère plus qu’un objet dont une variable
d’instance (privée) contient un int
(voir B.6.1.1).
Il existe deux méthodes pour convertir un scalaire int
en un objet Integer et réciproquement,
valueOf
(logiquement statique)
et intValue
(logiquement dynamique).
De sorte qu’écrire la calculatrice Calc
(voir 2.1.2) avec une pile de la bibliothèque semble assez lourd
au premier abord.
Mais en fait, le compilateur Java sait insérer les appels aux méthodes de conversion automatiquement, c’est-à-dire que l’on peut écrire plus directement.
Tout semble donc se passer presque comme si il y avait une pile
de int ; mais attention, il s’agit bien en fait d’une pile
de Integer.
Tout se passe plutôt comme si le compilateur
traduisait le programme avec les int vers le programme avec
les Integer, et c’est bien ce dernier qui s’exécute,
avec les conséquences prévisibles sur la performance en général et la
consommation mémoire en particulier.
Comme pour les piles, nous présentons trois techniques, tableaux, listes et bibliothèque.
L’idée, conceptuellement simple mais un peu délicate à programmer, est de gérer deux indices : in qui marque la position où ajouter le prochain élément et out qui marque la position d’où proviendra le prochain élément enlevé. L’indice out marque le début de la file et in sa fin. Autrement dit, le contenu de la file va la case d’indice out à la case qui précède la case d’indice in.
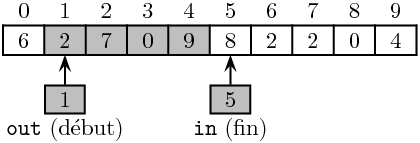
Dans le schéma ci-dessus, les cases valides sont grisées, de sorte que la file ci-dessus contient les entiers 2, 7, 0, 9 (dans l’ordre, 2 est le premier entré et 9 le dernier entré). Au cours de la vie de la file, les deux indices sont croissants. Plus précisément, on incrémente in après ajout et on incrémente out après suppression. Lorsqu’un indice atteint la fin du tableau, il fait tout simplement le tour du tableau et repart à zéro. Il en résulte que l’on peut avoir out < in. Par exemple, voici une autre file contenant cette fois 2, 0, 4, 6, 2, 7.

Le tableau d’une file est un tableau circulaire, que l’on parcourt en incrémentant un indice modulo n, où n est la taille du tableau. Par exemple pour parcourir le contenu de la file, on parcourt les indice de out à (in−1) mod n. Soit un parcours de 1 à 4 dans le premier exemple et de 7 à 2 dans le second.
Une dernière difficulté est de distinguer entre file vide et file pleine. Comme le montre le schéma suivant, les deux indices out et in n’y suffisent pas.

Ici, out (début) et in (fin) valent tous deux 4. Pour connaître le contenu de la file il faut donc parcourir le tableau de l’indice 4 à l’indice 3. Une première interprétation du parcours donne une file vide, et une seconde une file pleine.
class FifoEmpty extends Exception { }
class Fifo {
final static int SIZE=10 ;
private int in, out, nb ;
private int [] t ;
Fifo () { t = new int[SIZE] ; in = out = nb = 0 ; }
/* Increment modulo la taille du tableau t, utilisé partout */
private int incr(int i) { return (i+1) % t.length ; }
boolean isEmpty() { return nb == 0 ; }
int remove() throws FifoEmpty {
if (isEmpty()) throw new FifoEmpty () ;
int r = t[out] ;
out = incr(out) ; nb-- ; // Effectivement enlever
return r ;
}
void add(int x) {
if (nb+1 >= t.length) resize() ;
t[in] = x ;
in = incr(in) ; nb++ ; // Effectivement ajouter
}
private void resize() {
int [] newT = new int[2*t.length] ; // Allouer
int i = out ; // indice du parcours de t
for (int k = 0 ; k < nb ; k++) { // Copier
newT[k] = t[i] ;
i = incr(i) ;
}
t = newT ; out = 0 ; in = nb ; // Remplacer
}
/* Méthode toString, donne un exemple de parcours de la file */
public String toString() {
StringBuilder b = new StringBuilder () ;
b.append("[") ;
if (nb > 0) {
int i = out ;
b.append(t[i]) ; i = incr(i) ;
for ( ; i != in ; i = incr(i))
b.append(", " + t[i]) ;
}
b.append("]") ;
return b.toString() ;
}
}
On résout facilement la difficulté par une variable nb supplémentaire, qui contient le nombre d’éléments contenus dans la file. Une autre solution aurait été de décréter qu’une file qui contient n−1 éléments est pleine. On teste en effet cette dernière condition sans ambiguïté par in+1 congru à out modulo n. Nous choisissons la solution de la variable nb, car connaître simplement le nombre d’éléments de la file est pratique, notamment pour gérer le redimensionnement.
La figure 2.6 donne la classe Fifo des files
implémentées par un tableau, avec redimensionnement automatique.
Un point clé de ce code est la gestion des indices in et out.
Pour ajouter un élément dans la file, in est incrémenté
(modulo n). Par exemple, voici l’ajout (méthode add)
de l’entier 11 dans une file.

Pour supprimer un élément, on incrémente out. Par exemple, voici la suppression du premier élément d’une file (la méthode remove renvoie ici 2).

Le redimensionnement (méthode resize) a pour effet de tasser les éléments au début du nouveau tableau. Voici l’exemple de l’ajout de 13 dans une file pleine de taille 4.
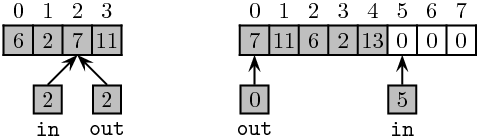
Avant ajout la file contient 7, 11, 6, 2, après ajout elle contient 7, 11, 6, 2, 13.
Le code du redimensionnement (méthode resize) est un peu simplifié par la présence de la variable nb. Pour copier les éléments de t dans newT, le contrôle est assuré par une simple boucle sur le compte des éléments transférés. Un contrôle sur l’indice i dans le tableau t serait plus délicat. La méthode toString donne un exemple de ce style de parcours du contenu de la file, entre les indices out (inclus) et in (exclu), qui doit particulariser le cas d’une file vide et effectuer la comparaison à in à partir du second élément parcouru (à cause du cas de la file pleine).
L’implémentation est conceptuellement simple. Les éléments de la file sont dans une liste, on enlève au début de la liste et on ajoute à la fin de la liste. Pour garantir des opérations en temps constant, on utilise une référence sur la dernière cellule de liste. Nous avons déjà largement exploité cette idée, par exemple pour copier une liste itérativement (voir l’exercice 1.2). Nous nous donnons donc une référence out sur la première cellule de la liste, et une référence in sur la dernière cellule.
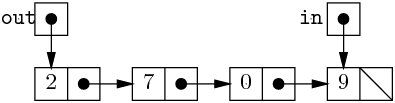
La file ci-dessus contient donc les entiers 2, 7, 0, 9 dans cette
ordre.
Une file vide est logiquement identifiée par une variable out
valant null. Par souci de cohérence in vaudra alors
aussi null.
On constate que le code est bien plus simple que dans le cas des
tableaux (figure 2.6).
La méthode remove est essentiellement la même que la
méthode pop des piles (voir 2.2.2),
car les deux méthodes réalisent la même
opération d’enlever le premier élément d’une liste.
La méthode add est à peine plus technique, voici par
exemple la suite des états mémoire quand on ajoute 3 à la file
déjà dessinée.
La première instruction List last = in garde une copie de
la référence in.
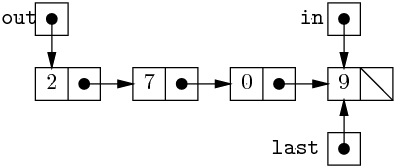
L’instruction suivante in = new List (x, null) alloue
la nouvelle cellule de liste.
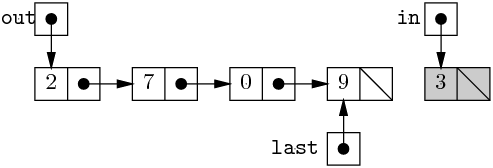
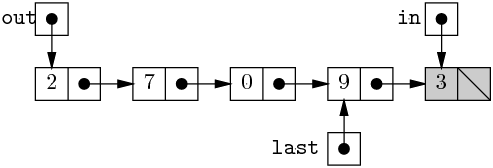
Et enfin, l’instruction last.next = in,
ajoute effectivement la nouvelle cellule pointée par in à la fin
de la liste-file.
Le package java.util de la bibliothèque offre plusieurs classes qui peuvent servir comme une file, même si nous ne respectons pas trop l’esprit dans lequel ces classes sont organisées. (Les files de la bibliothèque Queue ne sont pas franchement compatibles avec notre modèle simple des files).
Nous nous focalisons sur la classe LinkedList.
Comme le nom l’indique à peu près,
cette classe est implémentée par une liste chaînée.
Elle offre en fait bien plus que la simple fonctionnalité
de file, mais elle possède les méthodes
add
et remove
des files.
La classe LinkedList est générique, comme la classe Stack
de la section 2.2.3, ce qui la rend relativement simple
d’emploi.
LinkedList implémentent en fait les « queues à deux bouts »
(double ended queue), qui offrent deux couples de méthodes
addFirst/removeFirst et addLast/removeLast pour
ajouter/enlever respectivement au début et à la fin de queue.
Afin d’assurer des opérations en temps constant,
la classe de bibliothèque repose sur les listes doublement chaînées.
Voici
une classe DeList des cellules de liste doublement chaînée.
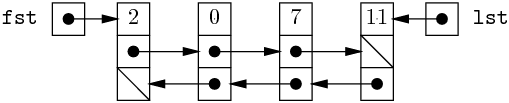
Décomposons une opération, par exemple addFirst, en ajoutant 3 au début de la queue déjà dessinée. Dans un premier temps on peut allouer la nouvelle cellule, avec un champ next correct (voir push en 2.2.2). Le champ prev peut aussi être initialisé immédiatement àclass DeQueue {
private DeList fst, lst ; // First and last cell
DeQueue () { fst = lst = null ; }
boolean isEmpty() { return fst == null ; }
void addFirst(int x) {
fst = new DeList(x, fst, null) ;
if (lst == null) {
lst = fst ;
} else {
fst.next.prev = fst ;
}
}
void addLast(int x) {
lst = new DeList(x, null, lst) ;
if (fst == null) {
fst = lst ;
} else {
lst.prev.next = lst ;
}
}
int removeFirst() {
if (fst == null) throw new Error ("removeFirst: empty queue") ;
int r = fst.val ;
fst = fst.next ;
if (fst == null) {
lst = null ;
} else {
fst.prev = null ;
}
return r ;
}
int removeLast() {
if (lst == null) throw new Error ("removeLast: empty queue") ;
int r = lst.val ;
lst = lst.prev ;
if (lst == null) {
fst = null ;
} else {
lst.next = null ;
}
return r ;
}
}
null.

fst.next
((fst.next).prev = fst).

lst (lst = lst.prev).
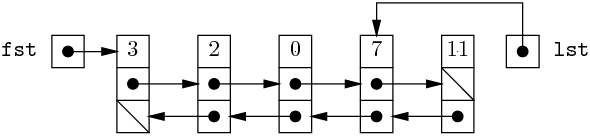
next de la nouvelle dernière
cellule (lst.next = null).
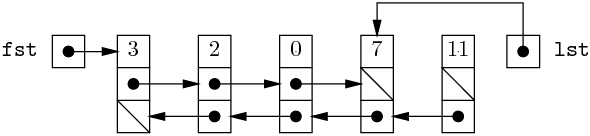
fst et lst tous deux égaux à null.
□Nous avons présenté trois façons d’implémenter piles et files. Il est naturel de se demander quelle implémentation choisir. Mais nous tenons d’abord à faire remarquer que, du strict point de vue de la fonctionnalité, la question ne se pose pas. Tout ce qui compte est d’avoir une pile (ou une file). En effet, les trois implémentations des piles offrent exactement le même service, de sorte que le choix d’une implémentation particulière n’a aucun impact sur le résultat d’un programme qui utilise une pile. La pile qui est définie exclusivement par les services qu’elle offre est un exemple de type de données abstrait.
Java offre des traits qui permettent de fabriquer des types abstraits
qui protègent leur implémentation des interventions intempestives.
Dans nos deux classes Stack, le tableau (ainsi que le
pointeur de pile sp) et la liste sont des champs privés.
Un programme qui utilise nos piles doit donc le faire exclusivement par
l’intermédiaire des méthodes push et pop. Champs privés et
méthodes accessibles correspondent directement à la notion de type
abstrait défini par les services offerts.
Il faut toutefois remarquer que, du point de vue du langage de
programmation, l’existence des deux (trois en fait) méthodes
reste pour le moment une convention : nous avons conventionnellement
appelé Stack la classe des piles et conventionnellement admis
qu’elle possède ces trois méthodes :
Il en résulte par exemple que nous ne pouvons pas encore mélanger les piles en tableau et les piles en liste dans le même programme, à moins de changer le nom des classes ce qui contredirait l’idée d’un type abstrait. Nous verrons au chapitre suivant comment procéder, à l’aide des interfaces.
Répondons maintenant sérieusement à la question du choix de l’implémentation. Dans disons 99 % des cas pour les files et 90 % des cas pour les piles, il faut choisir la classe de bibliothèque, parce que c’est la solution qui demande d’écrire le moins de code. La différence de pourcentage s’explique en comparant le temps de lecture de la documentation au temps d’écriture d’une classe des files ou des piles, et parce que la classe des piles est quand même simple à écrire.
La bibliothèque peut ne pas convenir pour des raisons d’efficacité :
le code est trop lent ou trop gourmand en mémoire pour notre programme
particulier et nous pouvons faire mieux que lui. Par exemple, le code
de bibliothèque entraîne la fabrication d’objets Integer en
pagaille, et une pile de scalaires se montre au final plus rapide. La
classe de bibliothèque peut aussi ne pas convenir parce qu’elle
n’offre pas la fonctionnalité inédite dont nous avons absolument besoin
(par exemple une inversion complète de la pile), ou plus fréquemment
parce que programmer cette fonctionnalité de la façon autorisée par la
structuration de la bibliothèque serait trop compliqué, trop coûteux,
ou tout simplement impossible avec notre connaissance limitée de Java.
Il reste alors à choisir entre tableaux et listes. Il n’y a pas de réponse toute faite à cette dernière question. En effet, d’une part, la difficulté de l’écriture d’un programme dépend aussi du goût et de l’expérience de chacun ; et d’autre part, l’efficacité respective de l’une ou de l’autre technique dépend de nombreux facteurs, (la pile croît-elle beaucoup, par exemple) et aussi de l’efficacité de la gestion de la mémoire par le système d’exécution de Java. Toutefois, dans le cas où le redimensionnement est inutile, le choix d’une pile-tableau s’impose probablement, puisque simplicité et efficacité concordent. Dans le cas général, on peut tout de même prévoir qu’utiliser les listes demande d’écrire un peu moins de code que d’utiliser les tableaux (redimensionnés). On peut aussi penser que les tableaux seront un plus efficaces que les listes, ou en tout cas utiliseront moins de mémoire au final. En effet, fabriquer une pile-tableau de N éléments demande d’allouer log2 N objets (tableaux) contre N objets (cellules de listes) pour une pile-liste. Or, allouer un objet est une opération chère.
Supposons qu’un objet occupe deux cases de mémoire en plus de l’espace nécessaire pour ses données (c’est une hypothèse assez probable pour Java). Une cellule de liste occupe donc 4 cases et un tableau de taille n occupe 3+n cases (dont une case pour la longueur). Pour un programme effectuant au total P push, la pile-liste aura alloué au total 4·P cases de mémoire, tandis que la pile-tableau aura alloué entre une (si la taille initiale du tableau est 1, et que le programme alterne push et pop) et environ 4·P + 3·log2 P cases de mémoire (dans le cas où aucun pop ne sépare les push et où le tableau est redimensionné par le dernier push). La pile-tableau n’alloue donc jamais significativement plus de mémoire que la pile-liste, et généralement plutôt moins.
Un autre coût intéressant est l’empreinte mémoire, la quantité de mémoire mobilisée à un instant donné. Une pile-file de N éléments mobilise 4·N cases de mémoire. Une pile-tableau mobilise entre 3+N et un nombre arbitrairement grand de cases de mémoire (le nombre arbitraire correspond à la taille du tableau lorsque, dans le passé, la pile a atteint sa taille maximale). Un nouvel élément intervient donc dans le choix de l’implémentation : la profondeur maximale de pile au cours de la vie du programme. Si cette profondeur reste raisonnable le choix de la pile-tableau s’impose, autrement le choix est moins net, mais la flexibilité de l’allocation petit-à-petit des cellules de la pile-liste est un avantage. On peut aussi envisager de réduire la taille du tableau interne de la pile tableau, par exemple en réduisant le tableau de la moitié de sa taille quand il n’est plus qu’au quart plein. Mais il faut alors y regarder à deux fois, notre classe des piles commence à devenir compliquée est tout ce code ajouté entraîne un prix en temps d’exécution.


