 |
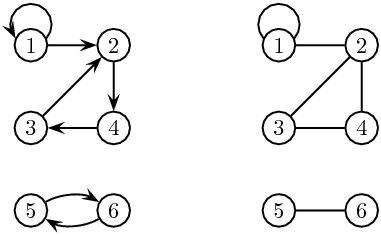
| Figure 4.1: À gauche un graphe, à droite un graphe non orienté. |



Ce chapitre est consacré aux arbres, l’un des concepts algorithmiques les plus importants de l’informatique. Les arbres servent à représenter un ensemble de données structurées hiérarchiquement. Plusieurs notions distinctes se cachent en fait sous cette terminologie: arbres libres, arbres enracinés, arbres binaires, etc. Ces définitions sont précisées dans la section 4.1.
Nous présentons plusieurs applications des arbres: les arbres de décision, les files de priorité, le tri par tas et l’algorithme baptisé « union-find », qui s’applique dans une grande variété de situations. Les arbres binaires de recherche seront traités dans le chapitre suivant.
Pour présenter les arbres de manière homogène, quelques termes empruntés aux graphes s’avèrent utiles. Nous présenterons donc les graphes, puis successivement, les arbres libres, les arbres enracinés et les arbres ordonnés.
Un graphe G = (S, A) est un couple formé d’un ensemble de nœuds S et d’un ensemble A d’arcs. L’ensemble A est une partie de S× S. Les nœuds sont souvent représentés par des points dans le plan, et un arc a = (s,t) par une ligne orientée joignant s à t. On dit que l’arc a part de s et va à t. Un chemin de s à t est une suite (s = s0, …, sn = t) de nœuds tels que, pour 1 ≤ i≤ n, (si−1, si) soit un arc. Le nœud s0 est l’origine du chemin et le nœud sn son extrémité. L’entier n est la longueur du chemin. C’est un entier positif ou nul. Un circuit est un chemin de longueur non nulle dont l’origine coïncide avec l’extrémité.
Figure 4.1: À gauche un graphe, à droite un graphe non orienté.
À côté de ces graphes, appelés aussi graphes orientés (« digraph » en anglais, pour « directed graph »), il existe la variante des graphes non orientés. Au lieu de couples de nœuds, on considère des paires {s, t} de nœuds. Un graphe non orienté est donné par un ensemble de ces paires, appelées arêtes. Les concepts de chemin et circuit se transposent sans peine à ce contexte.
Un chemin est simple si tous ses nœuds sont distincts. Un graphe est connexe si deux quelconques de ses nœuds sont reliés par un chemin.
Dans la suite de chapitre, nous présentons des familles d’arbres de plus en plus contraints. La famille la plus générale est formée des arbres libres. Un arbre libre est un graphe non orienté non vide, connexe et sans circuit. La proposition suivante est laissée en exercice.
Figure 4.2: Un arbre « libre ».
Un arbre enraciné ou arbre (« rooted tree » en anglais) est un arbre libre muni d’un nœud distingué, appelé sa racine. Soit T un arbre de racine r. Pour tout nœud x, il existe un chemin simple unique de r à x. Tout nœud y sur ce chemin est un ancêtre de x, et x est un descendant de y. Le sous-arbre de racine x est l’arbre contenant tous les descendants de x. L’avant-dernier nœud y sur l’unique chemin reliant r à x est le parent (ou le père ou la mère) de x, et x est un enfant (ou un fils ou une fille) de y. L’arité d’un nœud est le nombre de ses enfants. Un nœud sans enfant est une feuille, un nœud d’arité strictement positive est appelé nœud interne. La hauteur d’un arbre T est la longueur maximale d’un chemin reliant sa racine à une feuille. Un arbre réduit à un seul nœud est de hauteur 0.
Figure 4.3: Un arbre « enraciné ».
Les arbres admettent aussi une définition récursive. Un arbre sur un ensemble fini de nœuds est un couple formé d’un nœud particulier, appelé sa racine, et d’une partition des nœuds restants en un ensemble d’arbres. Par exemple, l’arbre de la figure 4.3 correspond à la définition
| T = ( 1, {(2, {(5),(6)}), (3, {(7),(8),(9)}), (4)}) |
Cette définition récursive est utile dans les preuves et dans la programmation. On montre ainsi facilement que si tout nœud interne d’un arbre est d’arité au moins 2, alors l’arbre a strictement plus de feuilles que de nœuds internes.
Une forêt est un ensemble d’arbres.
Un arbre ordonné est un arbre dans lequel l’ensemble des enfants de chaque nœud est totalement ordonné.
Figure 4.4: L’arbre ordonné de la table des matières d’un livre.
Par exemple, un livre, structuré en chapitres, sections, etc., se présente comme un arbre ordonné (voir figure 4.4). Les enfants d’un nœud d’un arbre ordonné sont souvent représentés, dans un programme, par une liste attachée au nœud. Un autre solution est d’associer, à chaque nœud, un tableau de fils. C’est une solution moins souple si le nombre de fils est destiné à changer. Enfin, on verra plus loin une autre représentation au moyen d’arbres binaires.
Comme premier exemple de l’emploi des arbres et des forêts, nous considérons un problème célèbre, et à ce jour pas encore entièrement résolu, appelé le problème Union-Find. Rappelons qu’une partition d’un ensemble E est un ensemble de parties non vides de E, deux à deux disjointes et dont la réunion est E. Étant donné une partition de l’ensemble {0,…, n−1}, on veut résoudre les deux problèmes que voici:
Nous donnons d’abord une solution du problème Union-Find, puis nous donnerons quelques exemples d’application.
En général, on part d’une partition où chaque classe est réduite à un singleton, puis on traite une suite de requêtes de l’un des deux types ci-dessus.
Avant de traiter ce problème, il faut imaginer la façon de représenter une partition. Une première solution consiste à représenter la partition par un tableau classe. Chaque classe est identifiée par un entier par exemple, et classe[x] contient le numéro de la classe de l’élément x (cf. figure 4.5).
x classe[x] 2 3 1 4 4 1 2 4 1 4
Figure 4.5: Tableau associé à la partition {{2,5,8},{0,6},{1},{3,4,7,9}}.
Trouver la classe d’un élément se fait en temps constant, mais fusionner deux classes prend un temps O(n), puisqu’il faut parcourir tout le tableau pour repérer les éléments dont il faut changer la classe. Une deuxième solution, que nous détaillons maintenant, consiste à choisir un représentant dans chaque classe. Fusionner deux classes revient alors à changer de représentant pour les éléments de la classe fusionnée. Il apparaît avantageux de représenter la partition par une forêt. Chaque classe de la partition constitue un arbre de cette forêt. La racine de l’arbre est le représentant de sa classe. La figure 4.6 montre la forêt associée à une partition.
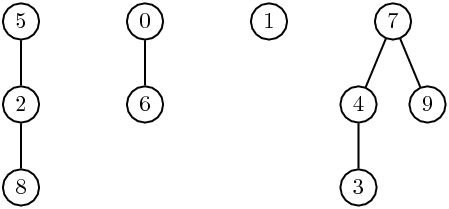
Figure 4.6: Forêt associée à la partition {{2,5,8},{0,6},{1},{3,4,7,9}}.
Une forêt est représentée par un tableau d’entiers pere (cf. Figure 4.7). Chaque nœud est représenté par un entier, et l’entier pere[x] est le père du nœud x. Une racine r n’a pas de parent. On convient que, dans ce cas, pere[r] = r.
x pere[x] 0 1 5 4 7 5 0 7 2 7
Figure 4.7: Tableau associé à la forêt de la figure 4.6.
On suppose donc défini un tableau
int[] pere = new int[n];
Ce tableau est initialisé à l’identité par
static void initialisation()
{
for (int i = 0; i < pere.length ; i++)
pere[i] = i;
}
Chercher le représentant de la classe contenant un élément donné revient à trouver la racine de l’arbre contenant un nœud donné. Ceci se fait par la méthode suivante:
static int trouver(int x)
{
while (x != pere[x])
x = pere[x];
return x;
}
L’union de deux arbres se réalise en ajoutant la racine de l’un des deux arbres comme nouveau fils à la racine de l’autre:
static void union(int x, int y)
{
int r = trouver(x);
int s = trouver(y);
if (r != s)
pere[r] = s;
}
Figure 4.8: La forêt de la figure 4.6 après l’union pondérée de 5 et 0.
Il n’est pas difficile de voir que chacune de ces deux méthodes est de complexité O(h), où h est la hauteur l’arbre (la plus grande des hauteurs des deux arbres). En fait, on peut améliorer l’efficacité de l’algorithme par la règle suivante (voir figure 4.8):
Règle. Lors de l’union de deux arbres, la
racine de l’arbre de moindre taille devient fils de la racine de l’arbre de
plus grande taille.
Pour mettre en œuvre cette stratégie, on utilise un tableau supplémentaire qui mémorise la taille des arbres, qui doit être initialisé à 1:
int[] taille = new int[n];
La nouvelle méthode d’union s’écrit alors:
static void unionPondérée(int x, int y)
{
int r = trouver(x);
int s = trouver(y);
if (r == s)
return;
if (taille[r] > taille[s])
{
pere[s] = r;
taille[r] += taille[s];
}
else
{
pere[r] = s;
taille[s] += taille[r];
}
}
L’intérêt de cette méthode vient de l’observation suivante:
| max(1+⌊log2(n−m)⌋, 2 + ⌊log2 m⌋) . |
Figure 4.9: « Trouver » 10 avec compression du chemin.
Une deuxième stratégie, appliquée cette fois-ci lors de la méthode trouver permet une nouvelle amélioration considérable de la complexité. Elle est basée sur la règle de compression de chemins suivante:
Règle. Après être remonté du nœud x à sa
racine r, on refait le parcours en faisant de chaque nœud rencontré un
fils de r.
La figure 4.9 montre la transformation d’un arbre par une compression de chemin. Chacun des nœuds 10 et 4 devient fils de 1. L’implantation de cette règle se fait simplement.
static int trouverAvecCompression(int x)
{
int r = trouver(x);
while (x != r)
{
int y = pere[x];
pere[x] = r;
x = y;
}
return r;
}
L’ensemble des deux stratégies permet d’obtenir une complexité presque linéaire.
En fait, on a α(n,m)≤ 2 pour m≥ n et n < 265536 et par conséquent, l’algorithme précédent se comporte, d’un point de vue pratique, comme un algorithme linéaire en n + m. Pourtant, Tarjan a montré qu’il n’est pas linéaire et on ne connaît pas à ce jour d’algorithme linéaire.
Un premier exemple est la construction d’un arbre couvrant un graphe donné. Au départ, chaque nœud constitue à lui seul un arbre. On prend ensuite les arêtes, et on fusionne les arbres contenant les extrémités de l’arête si ces extrémités appartiennent à des arbres différents.
Un second exemple concerne les problèmes de connexion dans un réseau. Voici un exemple de tel problème. Huit ordinateurs sont connectés à travers un réseau. L’ordinateur 1 est connecté au 3, le 2 au 3, le 5 au 4, le 6 au 3, le 7 au 5, le 1 au 6 et le 7 au 8. Est-ce que les ordinateurs 4 et 6 peuvent communiquer à travers le réseau? Certes, il n’est pas très difficile de résoudre ce problème à la main, mais imaginez la même question pour un réseau dont la taille serait de l’ordre de plusieurs millions. Comment résoudre ce problème efficacement? C’est la même solution que précédemment! On considère le réseau comme un graphe dont les nœuds sont les ordinateurs. Au départ, chaque nœud constitue à lui seul un arbre. On prend ensuite les arêtes (i.e. les connexions entre deux ordinateurs), et on fusionne les arbres contenant les extrémités de l’arête si ces extrémités appartiennent à des arbres différents.
La notion d’arbre binaire est assez différente des définitions précédentes. Un arbre binaire sur un ensemble fini de nœuds est soit vide, soit l’union disjointe d’un nœud appelé sa racine, d’un arbre binaire appelé sous-arbre gauche, et d’un arbre binaire appelé sous-arbre droit. Il est utile de représenter un arbre binaire non vide sous la forme d’un triplet A= (Ag, r, Ad).
Figure 4.10: Deux arbres binaires différents.
Par exemple, l’arbre binaire sur la gauche de la figure 4.10 est (∅, 1 , ( (∅, 3, ∅), 2, ∅ )), alors que l’arbre sur la droite de la figure 4.10 est ((∅, 2, (∅, 3, ∅)), 1, ∅). Cet exemple montre qu’un arbre binaire n’est pas simplement un arbre ordonné dont tous les nœuds sont d’arité au plus 2.
La distance d’un nœud x à la racine ou la profondeur de x est égale à la longueur du chemin de la racine à x. La hauteur d’un arbre binaire est égale à la plus grande des distances des feuilles à la racine.
Un arbre binaire est complet si tout nœud a 0 ou 2 fils.
Le résultat est vrai pour l’arbre binaire de hauteur 0. Considérons un arbre binaire complet A= (Ag, r, Ad). Les feuilles de A sont celles de Ag et de Ad et donc f(A) = f(Ag) + f(Ad). Les nœuds internes de A sont ceux de Ag, ceux de Ad et la racine, et donc n(A) = n(Ag) + n(Ad) + 1. Comme Ag et Ad sont des arbres complets de hauteur inférieure à celle de A, la récurrence s’applique et on a f(Ag) = n(Ag) + 1 et f(Ad) = n(Ad) + 1. On obtient finalement f(A) = f(Ag) + f(Ad) = (n(Ag) + 1) + (n(Ad) + 1) = n(A) + 1. □
On montre aussi que, dans un arbre binaire complet, il y a un nombre pair de nœuds à chaque niveau, sauf au niveau de la racine.
La figure 4.11 montre les arbres binaires ayant 1, 2, 3 et 4 nœuds.
Figure 4.11: Les premiers arbres binaires.
Notons bn le nombre d’arbres à n nœuds. On a donc b0=b1=1, b2=2, b3=5, b4=14. Comme tout arbre A non vide s’écrit de manière unique sous forme d’un triplet (Ag, r, Ad), on a pour n≥ 1 la formule
| bn= |
| bibn−i−1 |
La série génératrice B(x) = ∑n≥ 0bnxn vérifie donc l’équation
| xB2(x) −B(x) +1 = 0 . |
Comme les bn sont positifs, la résolution de cette équation donne
| bn= |
|
| = |
|
Les nombres bn sont connus comme les nombres de Catalan. L’expression donne aussi bn ∼ π−1/2·4n·n−3/2 + O(4n·n−5/2).
Nous présentons quelques concepts sur les mots qui servent à plusieurs reprises. D’abord, ils mettent en évidence des liens entre les parcours d’arbres binaires et certains ordres. Ensuite, ils seront employés dans des algorithmes de compression.
Un alphabet est un ensemble de lettres, comme {0,1} ou {a, b, c, d, r}. Un mot est une suite de lettres, comme 0110 ou abracadabra. La longueur d’un mot u, notée |u|, est le nombre de lettres de u: ainsi, |0110|=4 et |abracadabra|=11. Le mot vide, de longueur 0, est noté ε. Etant donnés deux mots, le mot obtenu par concaténation est le mot formé des deux mots juxtaposés. Le produit de concaténation est noté comme un produit. Si u=abra et v=cadabra, alors uv = abracadabra. Un mot p est préfixe (propre) d’un mot u s’il existe un mot v (non vide) tel que u = pv. Ainsi, ε, abr, abrac sont des préfixes propres de abraca. Un ensemble de mots P est préfixiel si tout préfixe d’un mot de P est lui-même dans P. Par exemple, les ensembles {ε, 1, 10, 11} et {ε, 0, 00, 01, 000, 001} sont préfixiels.
Un ordre total sur l’alphabet s’étend en un ordre total sur l’ensemble des mots de multiples manières. Nous considérons deux ordres, l’ordre lexicographique et l’ordre des mots croisés (« radix order » ou « shortlex » en anglais).
L’ordre lexicographique, ou ordre du dictionnaire, est défini par u <lex v si seulement si u est préfixe de v ou u et v peuvent s’écrire u= pau′, v=pbv′, où p est un mot, a et b sont des lettres, et a<b. L’ordre des mots croisés est défini par u <mc v si et seulement si |u| < |v| ou |u| = |v| et u <lex v. Par exemple, on a
| bar <mc car <mc barda <mc radar <mc abracadabra |
Chaque arête (p,f) d’un arbre A binaire est étiquetée par 0 si f est fils gauche de p, et par 1 si f est fils droit. L’étiquette du chemin qui mène de la racine à un nœud est le mot formé des étiquettes de ses arêtes. Le code de l’arbre A est l’ensemble des étiquettes des chemins issus de la racine. Cet ensemble est clairement préfixiel, et réciproquement, tout ensemble fini préfixiel de mots formés de 0 et 1 est le code d’un arbre binaire. La correspondance est, de plus, bijective.
Figure 4.12: Le code de l’arbre est {ε, 0, 1, 00, 01, 10, 11, 010, 101, 110}.
Le code c(A) d’un arbre binaire A se définit d’ailleurs simplement par récurrence: on a c(∅)={ε} et si A = (Ag, r, Ad), alors c(A) = 0c(Ag)∪{ε}∪1c(Ad).
Un parcours d’arbre est une énumération des nœuds de l’arbre. Chaque parcours définit un ordre sur les nœuds, déterminé par leur ordre d’apparition dans cette énumération.
On distingue les parcours de gauche à droite, et les parcours de droite à gauche. Dans un parcours de gauche à droite, le fils gauche d’un nœud précède le fils droit (et vice-versa pour un parcours de droite à gauche). Ensuite, on distingue les parcours en profondeur et en largeur.
Le parcours en largeur énumère les nœuds niveau par niveau. Ainsi, le parcours en largeur de l’arbre 4.13 donne la séquence a, b, c, d, e, f, g, h, i, k. On remarque que les codes des nœuds correspondants, ε, 0, 1, 00, 01, 10, 11, 010, 101, 110, sont en ordre croissant pour l’ordre des mots croisés. C’est en fait une règle générale.
Règle. L’ordre du parcours en largeur
correspond à l’ordre des mots croisés sur le code de l’arbre.
On définit trois parcours en profondeur privilégiés qui sont
Les ordres correspondant sont appelés ordres préfixe, infixe et suffixe. Considérons l’arbre de la figure 4.13.

Figure 4.13: Un arbre binaire. Les nœuds sont nommés par des lettres.
Le parcours préfixe donne les nœuds dans l’ordre a, b, d, e, h, c, f, i, g, k, le parcours infixe donne la suite d, b, h, e, a, f, i, c, k, g et le parcours suffixe donne d, h, e, b, i, f, k, g, c, a. De manière formelle, les parcours préfixe (infixe, suffixe) sont définis comme suit. Si A est l’arbre vide, alors pref(A) = inf(A) = suff(A) = ε; si A = (Ag, r, Ad), et e(r) est le nom de r, alors
|
Règle. Le parcours préfixe d’un arbre
correspond à l’ordre lexicographique sur le code de l’arbre. Le parcours
suffixe correspond à l’opposé de l’ordre lexicographique si l’on convient
que 1 < 0.
Qu’on se rassure, il y a aussi une interprétation pour le parcours infixe, mais elle est un peu plus astucieuse! À chaque nœud x de l’arbre, on associe un nombre formé du code du chemin menant à x, suivi de 1. Ce code complété est interprété comme la partie fractionnaire d’un nombre entre 0 et 1, écrit en binaire. Pour l’arbre de la figure 4.13, les nombres obtenus sont donnés dans la table suivante
|
L’ordre induit sur les mots est appelé l’ordre fractionnaire.
Règle. L’ordre infixe correspond à l’ordre
fractionnaire sur le code de l’arbre.
La programmation de ces parcours sera donnée au chapitre 5.
Voici une application surprenante des arbres à l’analyse de complexité. Il existe de nombreux algorithmes de tri, certains dont la complexité dans le pire des cas est en O(n2) comme les tris par sélection, par insertion ou à bulles, d’autres en O(n3/2) comme le tri Shell, et d’autres en O(nlogn) comme le tri fusion ou le tri par tas, que nous verrons page ??. On peut se demander s’il est possible de trouver un algorithme de tri de complexité inférieure dans le pire des cas.
Avant de résoudre cette question, il faut bien préciser le modèle de calcul que l’on considère. Un tri par comparaison est un algorithme qui trie en n’utilisant que des comparaisons. On peut supposer que les éléments à trier sont deux-à-deux distincts. Le modèle utilisé pour représenter un calcul est un arbre de décision. Chaque comparaison entre éléments d’une séquence à trier est représentée par un nœud interne de l’arbre. Chaque nœud pose une question. Le fils gauche correspond à une réponse négative, le fils droit à une réponse positive (figure 4.14).
Figure 4.14: Exemple d’arbre de décision pour le tri.
Les feuilles représentent les permutations des éléments à effectuer pour obtenir la séquence triée. Le nombre de comparaisons à effectuer pour déterminer cette permutation est égale à la longueur du chemin de la racine à la feuille.
Nous prouvons ici:
Deux précisions pour clore cette parenthèse sur les tris. Tout d’abord, le résultat précédent n’est plus garanti si l’on change de modèle. Supposons par exemple que l’on veuille classer les notes (des entiers entre 0 et 20) provenant d’un paquet de 400 copies. La façon la plus simple et la plus efficace consiste à utiliser un tableau T de taille 21, dont chaque entrée T[i] sert à compter les notes égales à i. Il suffit alors de lire les notes une par une et d’incrémenter le compteur correspondant. Une fois ce travail accompli, le tri est terminé: il y a T[0] notes égales à 0, suivi de T[1] notes égales à 1, etc. Cet algorithme est manifestement linéaire et ne fait aucune comparaison! Pourtant, il ne contredit pas notre résultat. Nous avons en effet utilisé implicitement une information supplémentaire: toutes les valeurs à trier appartiennent à l’intervalle [0, 20]. Cet exemple montre qu’il faut bien réfléchir aux conditions particulières avant de choisir un algorithme.
Seconde remarque, on constate expérimentalement que l’algorithme de tri rapide (QuickSort), dont la complexité dans le pire des cas est en O(n2), est le plus efficace en pratique. Comment est-ce possible? Tout simplement parce que notre résultat ne concerne que la complexité dans le pire des cas. Or QuickSort est un algorithme en O(nlogn) en moyenne.
Considérons une définition des expressions arithmétiques avec un œil neuf. Une expression arithmétique e est :
L’œil neuf ne voit pas cette définition comme celle de l’écriture usuelle (notation infixe) des expressions, et d’ailleurs il manque les parenthèses. Il voit une définition inductive, l’ensemble des expressions est solution de cette équation récursive :
| E = ℤ ⋃ (E, +, E) ⋃ (E, -, E) ⋃ (E, *, E) ⋃ (E, /, E) |
Cette définition inductive est une définition d’arbre, les expressions sont des feuilles qui contiennent un entier ou des nœuds internes à deux fils. Voir une expression comme un arbre évite toutes les ambiguïtés de la notation infixe. Par exemple, les deux arbres de la figure 4.15 disent clairement quels sont les arguments des opérations + et * dans les deux cas.
Alors qu’en notation infixe, pour bien se faire comprendre, il faut écrire 1+(2*3) et (1+2)*3.
Dès qu’un programme doit faire des choses un tant soit peu compliquées avec les expressions arithmétiques, il faut représenter ces expressions par des arbres de syntaxe abstraite. Le terme « abstraite » se justifie par opposition à la syntaxe « concrète » qui est l’écriture des expressions, c’est-à-dire ici la notation infixe. La production des arbres de syntaxes abstraite à partir de la syntaxe concrète est l’analyse grammaticale (parsing), une question cruciale qui est étudiée dans le cours suivant INF 431.
Écrivons une classe Exp des cellules d’arbre des expressions.
Nous devons principalement distinguer cinq sortes de nœuds.
Les entiers, qui sont des feuilles, et les quatre opérations, qui ont deux
fils.
La technique d’implémentation la plus simple est de réaliser tous ces
nœuds par des objets d’une seule
classe Exp qui ont tous les champs nécessaires,
plus un champ tag qui indique la nature du nœud.1
Le champ tag contient un entier censé être
l’une de cinq constantes conventionnelles.
Ainsi pour construire l’arbre de gauche de la figure 4.15, on écrit :
C’est non seulement assez lourd, mais aussi source d’erreurs. On atteint ici la limite de ce qu’autorise la surcharge des constructeurs. Il est plus commode de définir cinq méthodes statiques pour construire les divers nœuds.
Et l’expression déjà vue, se construit par :
Ce qui est plus concis, sinon plus clair.
Un exemple d’opération « compliquée » sur les expressions
arithmétiques est le calcul de leur valeur.
L’opération n’est compliquée que si nous
essayons de l’effectuer directement sur les notations infixes, car sur
un arbre Exp c’est très facile.
L’instruction throw finale est nécessaire,
car le compilateur n’a pas de moyen de savoir que le champ tag
contient obligatoirement l’une des cinq constantes conventionnelles.
En son absence, le programme est rejeté par le compilateur.
Pour satisfaire le compilateur, on aurait aussi pu
renvoyer une valeur « bidon » par return 0, mais c’est nettement
moins conseillé. Une erreur est une erreur,
en cas d’arbre incorrect, mieux vaut tout arrêter que de faire
semblant de rien.
Dans cet exemple typique, il faut surtout remarquer le lien très fort entre la définition inductive de l’arbre et la structure récursive de la méthode. La programmation sur les arbres de syntaxe abstraite est naturellement récursive.
Nous avons déjà traité cette question de façon incomplète, en ne produisant que des notations infixes complètement parenthésées (exercice 2.2). Nous pouvons maintenant faire mieux.
L’idée est d’abord d’interpréter la notation postfixe comme un arbre, puis d’afficher cet arbre, en tenant compte des règles usuelles qui permettent de ne pas mettre toutes les parenthèses. Pour la première opération il ne faut se poser aucune question, nous reprenons le calcul des expressions données en notation postfixe (voir 2.1.2), en construisant un arbre au lieu de calculer une valeur. Nous avons donc besoin d’une pile d’arbres, ce qui est facile avec la classe des piles de la bibliothèque (voir 2.2.3).
Examinons
la question d’afficher un arbre Exp sous forme infixe
sans abuser des parenthèses.
Tout d’abord, les parenthèses autour d’un entier ne sont jamais
utiles.
Ensuite, on distingue deux classes d’opérateurs, les additifs
(+ et -) et les multiplicatifs (* et /),
les opérateurs d’une classe donnée ont le même comportement vis
à vis du parenthésage.
Il y a cinq positions possibles : au sommet de l’arbre,
et à gauche ou à droite d’un opérateur additif ou multiplicatif.
On examine ensuite l’éventuel parenthésage d’un opérateur.
Ceci nous conduit à regrouper les positions possible en trois classes
On identifie les trois classes par 1, 2 et 3. On voit alors que les additifs sont à parenthéser pour les classes strictement supérieures à 1, et les multiplicatifs pour les classes strictement supérieures à 2. Ce qui conduit directement à la méthode suivante qui prend en dernier argument un entier lvl qui rend compte de la position de l’arbre e à afficher dans la sortie out.
La méthode expToInfix mélange récursion et affichage. Cela ne pose pas de difficulté particulière : pour afficher une opération il faut d’abord afficher le premier argument (récursion) puis l’opérateur et enfin le second argument (récursion encore).
La sortie est un PrintWriter qui possède une
méthode print exactement comme System.out mais est bien
plus efficace (voir B.5.5.1).
Le code utilise une particularité de l’instruction switch :
on peut grouper les cas (ici des additifs et des multiplicatifs).
Pour afficher l’opérateur, on a recours à l’expression
conditionnelle (voir B.7.2).
Par exemple e.tag == ADD ? '+' : '-' vaut '+'
si e.tag est égal à ADD et '-' autrement —
et ici « autrement » signifie nécessairement que e.tag
est égal à SUB puisque nous sommes dans un cas regroupé
du switch ne concernant que ADD et SUB.
Voici finalement la méthode main de la classe Exp
qui appelle l’affichage infixe sur l’arbre construit en lisant la
notation postfixe
Les PrintWriter sont bufferisés, il faut
vider le tampon par out.flush() avant de finir,
voir B.5.4.
Reprenons l’exemple de la figure 2.4.
% java Exp 6 3 2 - 1 + / 9 6 - '*' 6/(3-2+1)*(9-6)
Ce qui est meilleur que l’affichage ((6/((3-2)+1))*(9-6)) de l’exercice 2.2. Le source complet de cet exemple est Exp.java.
Nous avons déjà rencontré les files d’attente. Les files de priorité sont des files d’attente où les éléments ont un niveau de priorité. Le passage devant le guichet, ou le traitement de l’élément, se fait en fonction de son niveau de priorité. L’implantation d’une file de priorité est un exemple d’utilisation d’arbre, et c’est pourquoi elle trouve naturellement sa place ici.
De manière plus formelle, une file de priorité est un type abstrait de données opérant sur un ensemble ordonné, et muni des opérations suivantes:
Bien sûr, on peut remplacer « le plus grand élément » par « le plus petit élément » en prenant l’ordre opposé. Plusieurs implantations d’une file de priorité sont envisageables: par tableau ou par liste, ordonnés ou non. Nous allons utiliser des tas. La table 4.1 présente la complexité des opérations des files de priorités selon la structure de données choisie.
Implantation Trouver max Insérer Retirer max Tableau non ordonné O(n) O(1) O(n) Liste non ordonnée O(n) O(1) O(1)a Tableau ordonné O(1) O(n) O(1) Liste ordonnée O(1) O(n) O(1) Tas O(1) O(logn) O(logn)
- a
Tableau 4.1: Complexité des implantations de files de priorité.
Un arbre binaire est tassé si son code est un segment initial pour l’ordre des mots croisés. En d’autres termes, dans un tel arbre, tous les niveaux sont entièrement remplis à l’exception peut-être du dernier niveau, et ce dernier niveau est rempli « à gauche ». La figure 4.16 montre un arbre tassé.
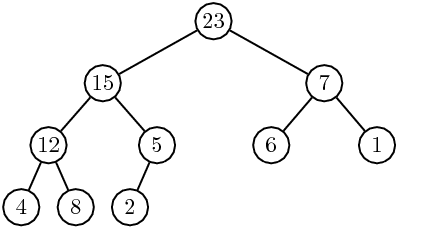
Figure 4.16: Un arbre tassé.
Un tas (en anglais « heap ») est un arbre binaire tassé tel que le contenu de chaque nœud soit supérieur ou égal à celui de ses fils. Ceci entraîne, par transitivité, que le contenu de chaque nœud est supérieur ou égal à celui de ses descendants.
L’arbre de la figure 4.16 est un tas.
Un tas s’implante facilement à l’aide d’un simple tableau. Les nœuds d’un arbre tassé sont numérotés en largeur, de gauche à droite. Ces numéros sont des indices dans un tableau (cf figure 4.17).
Figure 4.17: Un arbre tassé, avec la numérotation de ses nœuds.
L’élément d’indice i du tableau est le contenu du nœud de numéro i. Dans notre exemple, le tableau est:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Le fait que l’arbre soit tassé conduit à un calcul très simple des relations de filiation dans l’arbre (n est le nombre de ses nœuds):
|
L’insertion d’un nouvel élément v se fait en deux temps: d’abord, l’élément est ajouté comme contenu d’un nouveau nœud à la fin du dernier niveau de l’arbre, pour que l’arbre reste tassé. Ensuite, le contenu de ce nœud, soit v, est comparé au contenu de son père. Tant que le contenu du père est plus petit que v, le contenu du père est descendu vers le fils. À la fin, on remplace par v le dernier contenu abaissé (voir figure 4.18).
Figure 4.18: Un tas, avec remontée de la valeur 21 après insertion.
La suppression se fait de manière similaire. D’abord, le contenu du nœud le plus à droite du dernier niveau est transféré vers la racine, et ce nœud est supprimé. Ceci garantit que l’arbre reste tassé. Ensuite, le contenu v de la racine est comparé à la plus grande des valeurs de ses fils (s’il en a). Si cette valeur est supérieure à v, elle est remontée et remplace le contenu du père. On continue ensuite avec le fils. Par exemple, la suppression de 16 dans l’arbre de gauche de la figure 4.19 conduit d’abord à l’arbre de droite de cette figure, et enfin au tas de la figure 4.20
Figure 4.19: Un tas, et la circulation des valeurs pendant la suppression de 16.
Figure 4.20: Le tas de la figure 4.19 après suppression de 16.
La complexité de chacune de ces opérations est majorée par la hauteur de l’arbre qui est, elle, logarithmique en la taille.
Un tas est naturellement présenté comme une classe, fournissant les trois méthodes maximum(), inserer(), supprimer(). On range les données dans un tableau interne. Un constructeur permet de faire l’initialisation nécessaire. Voici le squelette:
class Tas
{
int[] a;
int nTas = 0;
Tas(int n)
{
nTas = 0;
a = new int[n];
}
int maximum()
{
return a[0];
}
void ajouter(int v) {...}
void supprimer() {...}
Avant de donner l’implantation finale, voici une première version à l’aide de méthodes qui reflètent les opérations de base.
void ajouter(int v)
{
int i = nTas;
++nTas;
while (!estRacine(i) && cle(parent(i)) < v)
{
cle(i) = cle(parent(i));
i = parent(i);
}
cle(i) = v;
}
De même pour la suppression:
void supprimer()
{
--nTas;
cle(0) = cle(nTas);
int v = cle(0);
int i = 0;
while (!estFeuille(i))
{
int j = filsG(i);
if (existeFilsD(i) && cle(filsD(i)) > cle(filsG(i)))
j = filsD(i);
if (v >= cle(j)) break;
cle(i) = cle(j);
i = j;
}
cle(i) = v;
}
Il ne reste plus qu’à remplacer ce pseudo-code par les instructions opérant directement sur le tableau.
void ajouter(int v)
{
int i = nTas;
++nTas;
while (i > 0 && a[(i-1)/2] <= v)
{
a[i] = a[(i-1)/2];
i = (i-1)/2;
}
a[i] = v;
}
On notera que, puisque la hauteur d’un tas à n nœuds est ⌊ log2 n⌋, le nombre de comparaisons utilisée par la méthode ajouter est en O(logn).
void supprimer()
{
int v = a[0] = a[--nTas];
int i = 0;
while (2*i + 1 < nTas)
{
int j = 2*i + 1;
if (j +1 < nTas && a[j+1] > a[j])
++j;
if (v >= a[j])
break;
a[i] = a[j];
i = j;
}
a[i] = v;
}
}Là encore, la complexité de la méthode supprimer est en O(logn).
On peut se servir d’un tas pour trier : on insère les éléments à trier dans le tas, puis on les extrait un par un. Ceci donne une méthode de tri appelée tri par tas (« heapsort » en anglais).
static int[] triParTas(int[] a)
{
int n = a.length;
Tas t = new Tas(n);
for (int i = 0; i < n; i++)
t.ajouter(a[i]);
for (int i = n - 1; i >= 0; --i)
{
int v = t.maximum();
t.supprimer();
a[i] = v;
}
return a;
}
La complexité de ce tri est, dans le pire des cas, en O(nlogn). En effet, on appelle n fois chacune des méthodes ajouter et supprimer.
Une variante des arbres tassés sert à la fusion de listes ordonnées. On est en présence de k suites de nombres ordonnées de façon décroissante (ou croissante), et on veut les fusionner en une seule suite croissante. Cette situation se présente par exemple lorsqu’on veut fusionner des données provenant de capteurs différents.
Un algorithme « naïf » opère de manière la suivante. À chaque étape, on considère le premier élément de chacune des k listes (c’est le plus grand dans chaque liste), puis on cherche le maximum de ces nombres. Ce nombre est inséré dans la liste résultat, et supprimé de la liste dont il provient. La recherche du maximum de k éléments coûte k−1 comparaisons. Si la somme des longueurs des k listes de données est n, l’algorithme naïf est donc de complexité O(nk).
Il semble plausible que l’on puisse gagner du temps en « mémorisant » les comparaisons que l’on a faites lors du calcul d’un maximum. En effet, lorsque l’on calcule le maximum suivant, seule une donnée sur les k données comparées a changé. L’ordre des k−1 autres éléments reste le même, et on peut économiser des comparaisons si l’on connaît cet ordre au moins partiellement. La solution que nous proposons est basée sur un tas qui mémorise partiellement l’ordre. On verra que l’on peut effectuer la fusion en temps O(k+nlogk). Le premier terme correspond au « prétraitement », c’est-à-dire à la mise en place de la structure particulière.
L’arbre de sélection est un arbre tassé à k feuilles. Chaque feuille est en fait une liste, l’une des k listes à fusionner (voir figure 4.21).
Figure 4.21: Un arbre de sélection pour 8 listes.
La hauteur de l’arbre est logk. Chaque nœud de l’arbre contient, comme clé, le maximum des clés de ses deux fils (ou le plus grand élément d’une liste). En particulier, le maximum des éléments en tête des k listes (en grisé sur la figure 4.21) se trouve logk fois dans l’arbre, sur les nœuds d’un chemin menant à la racine. L’extraction d’un plus grand élément se fait donc en temps constant. Cette extraction est suivie d’un mise-à-jour: En descendant le chemin dont les clés portent le maximum, on aboutit à la liste dont la valeur de tête est ce maximum. L’élément est remplacé, dans la liste, par son suivant. Ensuite, on remonte vers la racine en recalculant, pour chaque nœud rencontré, le valeur de la clé, avec la nouvelle valeur du fils mis-à-jour. À la racine, on trouve le nouveau maximum (voir figure 4.22).
Figure 4.22: Après extraction du plus grand élément et recalcul.
La mise-à-jour se fait donc en O(logk) opérations. La mise en place initiale de l’arbre est en temps k.
La compression des données est un problème algorithmique aussi important que le tri. On distingue la compression sans perte, où les données décompressées sont identiques aux données de départ, et la compression avec perte. La compression sans perte est importante par exemple dans la compression de textes, de données scientifiques ou du code compilé de programmes. En revanche, pour la compression d’images et de sons, une perte peut être acceptée si elle n’est pas perceptible, ou si elle est automatiquement corrigée par le récepteur.
Parmi les algorithmes de compression sans perte, on distingue plusieurs catégories: les algorithmes statistiques codent les caractères fréquents par des codes courts, et les caractères rares par des codes longs; les algorithmes basés sur les dictionnaires enregistrent toutes les chaînes de caractères trouvées dans une table, et si une chaîne apparaît une deuxième fois, elle est remplacée par son indice dans la table. L’algorithme de Huffman est un algorithme statistique. L’algorithme de Ziv-Lempel est basé sur un dictionnaire. Enfin, il existe des algorithmes « numériques ». Le codage arithmétique remplace un texte par un nombre réel entre 0 et 1 dont les chiffres en écriture binaire peuvent être calculés au fur et à mesure du codage. Le codage arithmétique repose aussi sur la fréquence des lettres. Ces algorithmes seront étudiés dans le cours 431 ou en majeure.
L’algorithme de Huffman est un algorithme statistique. Les caractères du texte clair sont codés par des chaînes de bits. Le choix de ces codes se fait d’une part en fonction des fréquences d’apparition de chaque lettre, de sorte que les lettres fréquentes aient des codes courts, mais aussi de façon à rendre le décodage facile. Pour cela, on choisit un code préfixe, au sens décrit ci-dessous. La version du codage de Huffman que nous détaillons dans cette section est le codage dit « statique »: les fréquences n’évoluent pas au cours de la compression, et le code reste fixe. C’est ce qui se passe dans les modems, ou dans les fax.
Une version plus sophistiquée est le codage dit « adaptatif », présenté brièvement dans la section 4.6.3. Dans ce cas, les fréquences sont mises à jour après chaque compression de caractère, pour chaque fois optimiser le codage.
Un ensemble P de mots non vides est un code préfixe si aucun des mots de P n’est préfixe propre d’un autre mot de P.
Par exemple, l’ensemble {0, 100, 101, 111, 1100, 1101} est un code préfixe. Un code préfixe P est complet si tout mot est préfixe d’un produit de mots de P. Le code de l’exemple ci-dessus est complet. Pour illustrer ce fait, prenons le mot 1011010101011110110011: il est préfixe du produit
| 101 · 101 · 0 · 101 · 0 · 111 · 10 · 1100 · 11 1 |
L’intérêt de ces définitions vient des propositions suivantes.
Rappelons qu’un arbre binaire est dit complet si tous ses nœuds internes ont arité 2.
La figure 4.23 reprend l’arbre de la figure 4.12. Le code des feuilles est préfixe, mais il n’est pas complet.
Figure 4.23: Le code des feuilles est {00, 010, 101, 110}.
En revanche, le code des feuilles de l’arbre de la figure 4.24 est complet.
Figure 4.24: Le code des feuilles est {00, 010, 011, 10, 11}.
Le codage d’un texte par un code préfixe (complet) se fait de la manière suivante: à chaque lettre est associée une feuille de l’arbre. Le code de la lettre est le code de la feuille, c’est-à-dire l’étiquette du chemin de la racine à la feuille. Dans le cas de l’arbre de la figure 4.24, on associe les lettres aux feuilles de la gauche vers la droite, ce qui donne le tableau de codage suivant:
|
Le codage consiste simplement à remplacer chaque lettre par son code. Ainsi, abracadabra devient 00 010 11 00 011 00 10 00 010 11 0. Le fait que le code soit préfixe permet un décodage instantané: il suffit d’entrer la chaîne caractère par caractère dans l’arbre, et de se laisser guider par les étiquettes. Lorsque l’on est dans une feuille, on y trouve le caractère correspondant, et on recommence à la racine. Quand le code est complet, on est sûr de pouvoir toujours décoder un message, éventuellement à un reste près qui est un préfixe d’un mot du code.
Le problème qui se pose est de minimiser la taille du texte codé. Avec le code donné dans le tableau ci-dessus, le texte abracadabra, une fois codé, est composé de 25 bits. Si l’on choisit un autre codage, comme par exemple
|
on observe que le même mot se code par 0 10 111 0 1101 0 1100 0 10 111 0 et donc avec 23 bits. Bien sûr, la taille du résultat ne dépend que de la fréquence d’apparition de chaque lettre dans le texte source. Ici, il y a 5 lettres a, 2 lettres b et r, et 1 fois la lettre c et d.
L’algorithme de Huffman construit un arbre binaire complet qui donne un code optimal, en ce sens que la taille du code produit est minimale parmi la taille de tous les codes produits à l’aide de codes préfixes complets.
La fréquence d’un arbre est, bien sûr, la somme des fréquences de ses feuilles. Voici une illustration de cet algorithme sur le mot abracadabra. La première étape conduit à la création des 5 arbres (feuilles) de la figure 4.25. Les feuilles des lettres c et d sont fusionnées (figure 4.26), puis cet arbre avec la feuille b (figure 4.27), etc. Le résultat est représenté dans la figure 4.29.
Figure 4.25: Les 5 arbres réduits chacun à une feuille.
Figure 4.26: Les feuilles des lettres c et d sont fusionnées.
Figure 4.27: L’arbre est fusionné avec la feuille de r.
Figure 4.28: La feuille de b est fusionnée avec l’arbre.
Figure 4.29: L’arbre après la dernière fusion.
Notons qu’il y a beaucoup de choix dans l’algorithme: d’une part, on peut choisir lequel des deux arbres devient sous-arbre gauche ou droit. Ensuite, les deux sous-arbres de fréquence minimale ne sont peut-être pas uniques, et là encore, il y a des choix pour la fusion. On peut prouver que cet algorithme donne un code optimal. Il en existe de nombreuses variantes. L’une d’elle consiste à grouper les lettres par deux (digrammes) ou même par bloc plus grands, notamment s’il s’agit de données binaires. Les techniques de compression avec dictionnaire (compression de Ziv-Lempel) ou le codage arithmétique donnent en général de meilleurs taux de compression.
Si le nombre de lettres figurant dans le texte est n, l’arbre de Huffman est de taille 2n−1. On le représente ici par un tableau pere, où, pour x≥ 0 et y>0 pere[x] = y si x est fils droit de y et pere[x] = -y si x est fils gauche de y. Chaque caractère c a une fréquence d’apparition dans le texte, notée freq[c]. Seuls les caractères qui figurent dans le texte, i.e. de fréquence non nulle, vont être représentés dans l’arbre.
La création de l’arbre est contrôlée par un tas (mais un « tas-min », c’est-à-dire un tas avec extraction du minimum). La clé de la sélection est la fréquence des lettres et la fréquence cumulée dans les arbres. Une autre méthode rencontrée est l’emploi de deux files.
Cette représentation des données est bien adaptée au problème considéré, mais est assez éloignée des représentations d’arbres que nous verrons dans le chapitre suivant. Réaliser une implantation à l’aide de cette deuxième représentation est un bon exercice.
La classe Huffman a deux données statiques: le tableau pere pour représenter l’arbre, et un tableau freq qui contient les fréquences des lettres dans le texte, et aussi les fréquences cumulées dans les arbres. On part du principe que les 26 lettres de l’alphabet peuvent figurer dans le texte (dans la pratique, on prendra plutôt un alphabet de 128 ou de 256 caractères).
class Huffman
{
final static int N = 26, M = 2*N - 1; // nombre de caractères
static int[] pere = new int[M];
static int[] freq = new int[M];
public static void main(String[] args)
{
String s = args[0];
calculFrequences(s);
creerArbre();
String[] table = faireTable();
afficherCode(s,table);
System.out.println();
}
}
La méthode main décrit l’opération: on calcule les fréquences des lettres, et le nombre de lettres de fréquence non nulle. On crée ensuite un tas de taille appropriée, avec le tableau des fréquences comme clés. L’opération principale est creerArbre() qui crée l’arbre de Huffman. La table de codage est ensuite calculée et appliquée à la chaîne à compresser.
Voyons les diverses étapes. Le calcul des fréquences et du nombre de lettres de fréquence non nulle ne pose pas de problème. On notera toutefois l’utilisation de la méthode charAt de la classe String, qui donne l’unicode du caractère en position i. Comme on a supposé que l’alphabet était a–z et que les unicodes de ces caractères sont consécutifs, l’expression s.charAt(i) - ’a’ donne bien le rang du i-ème caractère dans l’alphabet. Il faudrait bien sûr modifier cette méthode si on prenait un alphabet à 256 caractères.
static void calculFrequences(String s)
{
for (int i = 0; i < s.length(); i++)
freq[s.charAt(i) - 'a']++;
}
static int nombreLettres()
{
int n = 0;
for (int i = 0; i < N; i++)
if (freq[i] > 0)
n++;
return n;
}
La méthode de création d’arbre utilise très exactement l’algorithme exposé plus haut: d’abord, les lettres sont insérées dans le tas; ensuite, les deux éléments de fréquence minimale sont extraits, et un nouvel arbre, dont la fréquence est la somme des fréquences des deux arbres extraits, est inséré dans le tas. Comme il y a n feuilles dans l’arbre, il y a n−1 créations de nœuds internes.
static void creerArbre()
{
int n = nombreLettres();
Tas tas = new Tas(2*n-1, freq);
for (int i = 0; i < N; ++i)
if (freq[i] >0)
tas.ajouter(i);
for (int i = N; i < N+n-1; ++i)
{
int x = tas.minimum();
tas.supprimer();
int y = tas.minimum();
tas.supprimer();
freq[i] = freq[x] + freq[y];
pere[x] = -i;
pere[y] = i;
tas.ajouter(i);
}
}
Le calcul de la table de codage se fait par un parcours d’arbre:
static String code(int i)
{
if (pere[i] == 0) return "";
return code(Math.abs(pere[i])) + ((pere[i] < 0) ? "0" : "1");
}
static String[] faireTable()
{
String[] table = new String[N];
for (int i = 0; i < N; i++)
if (freq[i] >0)
table[i] = code(i);
return table;
}
Il reste à examiner la réalisation du « tas-min ». Il y a deux différences avec les tas déjà vus: d’une part, le maximum est remplacé par le minimum (ce qui est négligeable), et d’autre part, ce ne sont pas les valeurs des éléments eux-mêmes (les lettres du texte) qui sont utilisées comme comparaison, mais une valeur qui leur est associée (la fréquence de la lettre). Les méthodes des tas déjà vues se récrivent très facilement dans ce cadre.
class Tas
{
int[] a; // contient les caractères
int nTas = 0;
int[] freq; // contient les fréquences des caractères
Tas(int taille, int[] freq)
{
this.freq = freq;
nTas = 0;
a = new int[taille];
}
int minimum()
{
return a[0];
}
void ajouter(int v)
{
int i = nTas;
++nTas;
while (i > 0 && freq[a[(i-1)/2]] >= freq[v])
{
a[i] = a[(i-1)/2];
i = (i-1)/2;
}
a[i] = v;
}
void supprimer()
{
int v = a[0] = a[--nTas];
int i = 0;
while (2*i + 1 < nTas)
{
int j = 2*i + 1;
if (j +1 < nTas && freq[a[j+1]] < freq[a[j]])
++j;
if (freq[v] <= freq[a[j]])
break;
a[i] = a[j];
i = j;
}
a[i] = v;
}
}
Une fois la table du code calculée, encore faut-il la transmettre avec le
texte comprimé, pour que le destinaire puisse décompresser le message.
Transmettre la table telle quelle est redondant puisque l’on transmet tous
les chemins de la racine vers les feuilles. Il est plus économique de
faire un parcours préfixe de l’arbre, avec la valeur littérale des lettres
représentées aux feuilles. Par exemple, pour l’arbre de la
figure 4.29, on obtient la représentation
01[a]01[b]001[d]1[c]1[r]. Une méthode plus simple est de
transmettre la suite de fréquence, quitte au destinataire de reconstruire
le code. Cette deuxième méthode admet un raffinement (qui montre jusqu’où
peut aller la recherche de l’économie de place) qui consiste à non pas
transmettre les valeurs exactes des fréquences, mais une séquence de
fréquences fictives (à valeurs numériques plus petites, donc plus courtes à
transmettre) qui donne le même code de Huffman.
Figure 4.30: Deux suites de fréquences qui produisent le même arbre.
Par exemple, les deux arbres de la figure 4.30 ont des fréquences différentes, mais le même code. Il est bien plus économique de transmettre la suite de nombres 5,1,2,1,3 que la suite initiale 43, 13, 12, 14, 41.
Les inconvénients de la méthode de compression de Huffman sont connus:
Une version adaptative de l’algorithme de Huffman corrige ces défauts. Le principe est le suivant:
Evidemment, le code d’une lettre change en cours de transmission : quand la fréquence (relative) d’une lettre augmente, la longueur de son code diminue. Le code d’une lettre s’adapte à sa fréquence.
Figure 4.31: Un arbre de Huffman avec un parcours compatible.
Le destinataire du message compressé mime le codage de l’expéditeur: il maintient un arbre de Huffman qu’il met à jour comme l’expéditeur, et il sait donc à tout moment quel est le code d’une lettre.
Les deux inconvénients du codage de Huffman (statique) sont corrigés par cette version. Il n’est pas nécessaire de calculer globalement les fréquences des lettres du texte puisqu’elles sont mises à jour à chaque pas. Il n’est pas non plus nécessaire de transmettre la table de codage puisqu’elle est recalculée par le destinataire.
Il existe par ailleurs une version « simplifiée » du codage de Huffman où les fréquences utilisées pour la construction de l’arbre ne sont pas les fréquences des lettres du texte à comprimer, mais les fréquences moyennes rencontrées dans les textes de la langue considérée. Bien entendu, le taux de compression s’en ressent si la distribution des lettres dans le texte à comprimer s’écarte de cette moyenne. C’est dans ce cas que l’algorithme adaptatif s’avère particulièrement utile.
Notons enfin que le principe de l’algorithme adaptatif s’applique à tous les algorithmes de compression statistiques. Il existe, par exemple, une version adaptative de l’algorithme de compression arithmétique.
L’algorithme adaptatif opère, comme l’algorithme statique, sur un arbre. Aux feuilles de l’arbre se trouvent les lettres, avec leurs fréquences. Aux nœuds de l’arbre sont stockées les fréquences cumulées, c’est-à-dire la somme des fréquences des feuilles du sous-arbre dont le nœud est la racine (voir figure 4.31). L’arbre de Huffman est de plus muni d’une liste de parcours (un ordre total) qui a les deux propriétés suivantes:
On démontre que, dans un arbre de Huffman, on peut toujours trouver un ordre de parcours possédant ces propriétés. Dans la figure 4.31, les nœuds sont numérotés dans un tel ordre.
Figure 4.32: Après incrémentation de d (à gauche), et après permutation des nœuds (à droite).
L’arbre de Huffman évolue avec chaque lettre codée, de la manière suivante. Soit x le caractère lu dans le texte clair. Il correspond à une feuille de l’arbre. Le code correspondant est envoyé, puis les deux opérations suivantes sont réalisées.
La deuxième opération garantit que l’ordre reste compatible avec les fréquences.
Figure 4.33: Avant permutation des nœuds 8 et 9 (à gauche) , et arbre final (à droite).
Supposons que la lettre suivante du texte clair à coder, dans l’arbre de la figure 4.31, soit une lettre d. Le code émis est alors 1001. La fréquence de la feuille d est incrémentée. Le père de la feuille d a pour fréquence 5. Son numéro d’ordre est 4, et le plus grand nœud de fréquence 5 a numéro d’ordre 5. Les deux nœuds sont échangés (figure 4.32). De même, avant d’incrémenter le nœud de numéro 8, il est échangé avec le nœud de numéro 9, de même fréquence (figure 4.33). Ensuite, la racine est incrémentée.
Pour terminer, voici une table de quelques statistiques concernant l’algorithme de Huffman. Ces statistiques ont été obtenues à une époque où il y avait encore peu de données disponibles sous format électronique, et les contes de Grimm en faisaient partie... Comme on le voit, le taux de compression obtenu par les deux méthodes est sensiblement égal, car les données sont assez homogènes.
|
Si on utilise un codage par digrammes (groupe de deux lettres), les statistiques sont les suivantes:
|
On voit que le taux de compression est légèrement meilleur.


