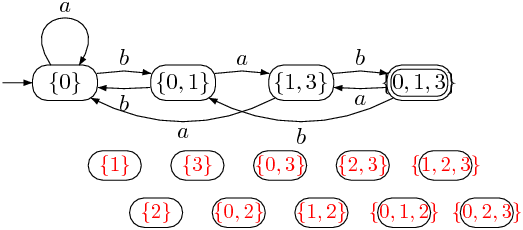Chapitre 7 Les automates

7.1 Pourquoi étudier les automates

Ce chapitre est une très succincte introduction à la théorie des automates que vous aurez l’occasion de voir de façon détaillée si vous choisissez un cursus d’informatique. Ce chapitre est, par nature, un peu plus “théorique” et un peu moins algorithmique que les précédents.

Les automates sont des objets mathématiques, très utilisés en informatique, qui permettent de modéliser un grand nombre de systèmes (informatiques). L’étude des automates a commencé vers la fin des années cinquante. Elle se base sur de nombreuses techniques (topologie, théorie des graphes, logique, algèbre, etc.). De façon très informelle, un automate est un ensemble “d’états du système”, reliés entre eux par des “transitions” qui sont marquées par des symboles. Étant donné un “mot” fourni en entrée, l’automate lit les symboles du mot un par un et va d’état en état selon les transitions. Le mot lu est soit accepté par l’automate soit rejeté.

Avant de donner une définition plus formelle des concepts décrits ci-dessus, citons quelques exemples classiques d’utilisation d’automates :

Vérification d’un circuit électronique
Recherche d’occurrence dans un texte (moteur de recherches sur le web, etc.)
Vérification de protocoles de communication
Compression de données
Compilation
Biologie (génomique)

En dehors de ces utilisations “pratiques” des automates, notons qu’ils sont aussi utilisés pour modéliser les ordinateurs et pour comprendre ce qu’un ordinateur peut faire (décidabilité) et ce qu’il sait faire efficacement (complexité). C’est donc une notion fondamentale de l’informatique.

7.2 Rappel : alphabets, mots, langages et problèmes

Nous reprenons ici les notations du chapitre 6. L’alphabet Σ est un ensemble de caractères (ou symboles). un mot est une suite finie de caractères. L’ensemble des mots sur Σ est noté Σ^*. Un langage est un sous-ensemble de Σ^*, c’est-à-dire un ensemble particulier de mots. Parmi les mots de Σ^* on distingue le mot vide noté є. Le mot vide est l’unique mot de longueur zéro.

7.3 Automates finis déterministes

Un automate fini déterministe est un quintuplé (Q, Σ, δ, q₀, F) constitué des éléments suivants

un alphabet fini (Σ)
un ensemble fini d’états (Q)
une fonction de transition (δ : Q * Σ → Q)
un état de départ (q₀ ∈ Q)
un ensemble d’états finaux (ou acceptant) F ⊆ Q

7.3.1 Fonctionnement d’un automate fini déterministe

L’automate prend en entrée un mot et l’accepte ou la rejette. On dit aussi qu’il le reconnaît ou ne le reconnaît pas. Le langage associé à un automate est constitué de l’ensemble des mots qu’il reconnaît. Voici comment l’automate procède pour décider si un mot appartient à son langage.

Le processus commence à l’état de départ q₀
Les symboles du mot sont lus les uns après les les autres.
À la lecture de chaque symbole, on emploie la fonction de transition δ pour se déplacer vers le prochain état (en utilisant l’état actuel et le caractère qui vient d’être lu).
le mot est reconnu si et seulement si le dernier état (i.e., l’état correspondant à la lecture du dernier caractère du mot) est un état de F.

De façon plus formelle, pour définir exactement le langage reconnu par un automate, nous introduisons la fonction de transition étendue aux mots, δ. Elle se définit récursivement comme suit.

A partir d’un état q en lisant le mot vide є on reste dans l’état q, i.e., ∀ q ∈ Q, δ(q, є) = q
Étant donné un mot c se terminant par a ∈ Σ (i.e., c = c′a avec c′ ∈ Σ ∪ {є}), et un état q de Q, δ(q, c) = δ(q, c′a) = δ(δ(q, c′), a)

Nous pouvons maintenant définir le langage L(A) accepté par un automate fini déterministe A = (Q, Σ, δ, q₀, F).

L(A) = {c | δ(q₀, c) ∈ F}

7.3.2 Des représentation “compactes” des automates

On peut associer à un automate une table de transition qui décrit de manière extensive la fonction de transition δ :

Une colonne correspond à un caractère de l’alphabet.
Une ligne correspond à un état de l’automate (l’état initial est précédé d’une flèche “→”; l’état final d’une étoile “*”)

La valeur δ(q, a) pour q ∈ Q, a ∈ Σ correspond à l’état indiqué à l’intersection de la ligne q et de la colonne a. Notons qu’à partir de cette table il est aisé de retrouver l’ensemble des états ainsi que l’alphabet et donc d’identifier exactement l’automate.

Exemple 7.1 Considérons la table de transition ci-dessous.

	a	b
→ 1	1	2
* 2	1	2

Il correspond à l’automate (Q, Σ, δ, q₀, F) avec

Q = {1, 2}
Σ = {a, b}
δ(1, a) = 1, δ(1, b) = 2, δ(2, a) = 1, δ(2, b) = 2
q₀ = 1
F = {2}

Il est facile de voir que le langage de cet automate est constitué exactement des mots composés de a et de b qui se terminent par un b.

Pour représenter de façon très intuitive un automate fini déterministe (Q, Σ, δ, q₀, F), on peut utiliser un graphe de transition constitué des éléments suivants :

Un ensemble de sommets (chaque sommet représente un élément de Q).
Un ensemble d’arcs entre les sommets valués par un symbole de σ (un arc entre les états q et q′ valué par le symbole s signifie que δ(q, s) = q′).
L’état initial q₀ est marqué par une flèche entrante.
Les états finaux F sont entourés d’une double ligne.

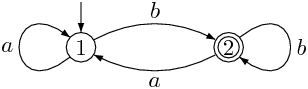
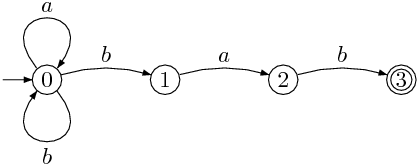
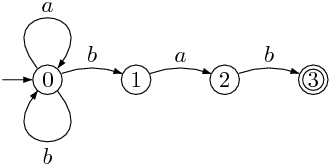
L’automate de l’exemple 7.1 est ainsi représenté sur la figure 7.1.

Figure 7.1: Un automate fini déterministe

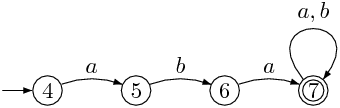
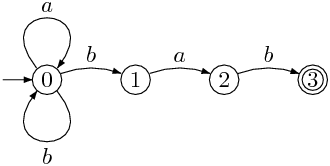
Pour simplifier encore cette représentation, un arc entre deux sommets q, q′ peut être valué par plusieurs symboles s₁, ..., s_n séparés par des virgules. Cette dernière convention signifie simplement que ∀ i ≤ n, δ(q, s_i) = q′ et elle permet d’éviter une multiplication d’arcs sur le graphe. La figure 7.2 illustre une telle simplification.

Figure 7.2: Deux représentations équivalentes du même automate fini

Exercice 7.1 Quel est le langage reconnu par l’automate de la figure 7.2 ?

Solution. Tous les mots qui contiennent un “b”. □

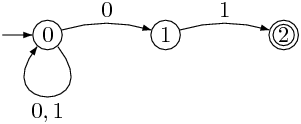
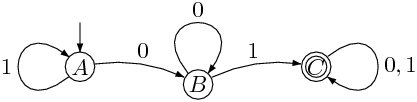
Exercice 7.2 Écrire la table de transition de l’automate suivant. Quel est le langage reconnu ?

Solution. La table de transition de l’automate est

	0	1
→ A	B	A
B	B	C
* C	C	C

Cet automate reconnaît les mots qui contiennent “01”. □

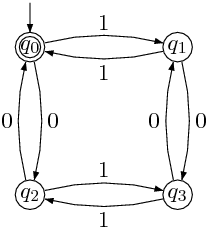
Exercice 7.3 Soit l’automate fini déterministe ({q₀, q₁ , q₂ , q₃}, {0, 1}, δ, q₀ , {q₀}) donné par la table

δ	0	1
→ * q₀	q₂	q₁
q₁	q₃	q₀
q₂	q₀	q₃
q₃	q₁	q₂

Dessiner l’automate et montrer qu’il accepte “110101”.

Solution.

□

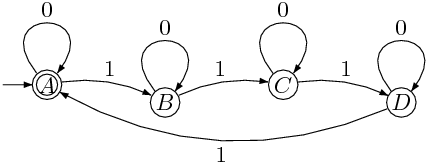
Exercice 7.4 Construire un automate fini déterministe qui reconnaît le langage

L = {x ∈ {0, 1}^* | n₁(x) ≡ 0 mod 4}

où n₁(x) est le nombre d’occurrence du symbole 1 dans le mot x.

Solution.

□

Exercice 7.5 Construire les automates finis déterministes qui reconnaissent les langages suivants

L₁ = {m ∈ (a + b)^* | chaque a de m est immédiatement précédé et immédiatement suivi d’un b }

L₂ = {m ∈ (a + b)^* | m contienne à la fois ab et ba }

L₃ = {m ∈ (a + b)^* | m contienne exactement une occurrence de aaa}

7.4 Automates finis non-déterministes

Un automate fini non-déterministe est un automate tel que dans un état donné, il peut y avoir plusieurs transitions avec le même symbole. le fonctionnement d’un tel automate n’est donc pas totalement « déterminé », car on ne sait pas quel état l’automate va choisir.

Les automates non-déterministes permettent de modéliser facilement des problèmes complexes. Ils peuvent être convertis en des automates finis déterministe. Ces derniers peuvent être exponentiellement plus grand que les automates non déterministe dont ils sont issus.

Un automate fini non-déterministe est un quintuplé : (Q, Σ, δ, q₀, F)

un alphabet fini (Σ)
un ensemble fini d’états (Q)
une fonction de transition δ qui associe à tout état q ∈ Q et tout symbole s ∈ Σ un sous ensemble de Q noté δ(q, s).
un état de départ (q₀)
un ensemble d’états finaux (ou acceptant) F

C’est la fonction de transition δ qui diffère ici de celle utilisée par les automates finis déterministes. Remarquons que tout automate fini déterministe est aussi un automate fini non-déterministe.

Les représentations compactes des automates finis déterministes s’étendent naturellement aux automates finis non-déterministes. Une cellule de la table de transition contient un sous-ensemble d’états (éventuellement vide).

7.4.1 Fonctionnement d’un automate fini non-déterministe

Comme pour un automate fini déterministe, l’automate prend en entrée un mot et l’accepte ou le rejette. Le langage associé est constitué de l’ensemble des mots qu’il reconnaît.

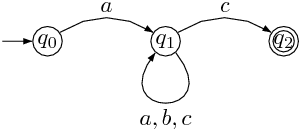
Exemple 7.2 Voici automate qui reconnaît les mots définis sur l’alphabet {a, b, c} qui commencent par a et qui finissent par c.

La table associée à cet automate est alors :

	a	b	c
→ q₀	{q₁}	∅	∅
q₁	{q₁}	{q₁}	{q₁, q₂}
* q₂	∅	∅	∅

Comme pour les automates déterministes, nous nous introduisons la fonction de transition étendue aux mots, δ. Elle se définit récursivement comme suit.

A partir d’un état q en lisant le mot vide є (le mot vide ne contient aucun symbole et est toujours noté є), on reste dans l’état q, i.e., ∀ q ∈ Q, δ(q, є) = {q}
Étant donné un mot c se terminant par a ∈ Σ (i.e., c = c′a avec c′ ∈ Σ ∪ {є}), et un état q de Q,
δ(q, c) = δ(q, c′a) =

∪

p ∈ δ(q, c′)

δ(p, a)

Nous pouvons maintenant définir le langage L(A) accepté par un automate fini déterministe A = (Q, Σ, δ, q₀, F).

L(A) = {c | δ(q₀, c) ⋂ F ≠ ∅}

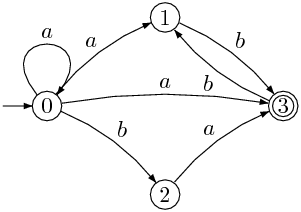
Exercice 7.6 Construire l’automate fini non-déterministe associé à la table ci-dessous.

	a	b
→ 0	{0,1, 3}	{2}
1	∅	{3}
2	{3}	∅
* 3	∅	{1}

Solution.

□

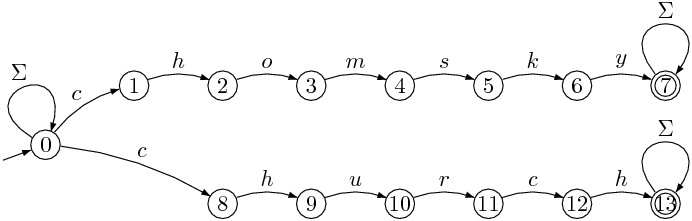
Exercice 7.7 Construire un automate fini non-déterministe qui reconnaît les mots qui contiennent “church” ou “chomsky”.

Solution.

□

Exercice 7.8 Construire un automate finis non-déterministe qui reconnaît les mots de l’alphabet {a,b} qui terminent par bab.

Solution.

□

Exercice 7.9 Construire un automate fini non-déterministe et un automate fini déterministe qui reconnaît les mots sur l’alphabet {a,b,c} décrits par l’expression régulière (a+b+c)^*b(a+b+c).

Exercice 7.10 Construire un automate fini non-déterministe qui reconnaît les nombres dont le dernier chiffre n’apparaît qu’une fois.

Exercice 7.11 Modélisation d’un jeu (d’après la page de Jean-Eric Pin). Le joueur a les yeux bandés. Face à lui, un plateau sur lequel sont disposés en carré quatre jetons, blancs d’un côté et noirs de l’autre. Le but du jeu est d’avoir les quatre jetons du côté blanc. Pour cela, le joueur peut retourner autant de jetons qu’il le souhaite, mais sans les déplacer. A chaque tour, le maître de jeu annonce si la configuration obtenue est gagnante ou pas, puis effectue une rotation du plateau de zéro, un, deux ou trois quarts de tours. La configuration de départ est inconnue du joueur, mais le maître de jeu annonce avant le début du jeu qu’elle n’est pas gagnante. Chaque annonce prend une seconde, et il faut 3 secondes au joueur pour retourner les jetons. Pouvez-vous aider le joueur à gagner en moins d’une minute ?

7.4.2 Déterminisation d’un automate fini non-déterministe

Un automate fini déterministe est aussi non-déterministe. Donc tout langage reconnu par un automate fini déterministe est reconnu par un automate fini non-déterministe. Plus surprenant, la réciproque est aussi vraie (Théorème de Rabin-Scott).

Considérons un automate fini non-déterministe A_n = (Q_n, Σ, δ_n, q₀, F_n) et construisons un automate fini déterministe A_d = (Q_d, Σ, δ_d, {q₀}, F_d) qui reconnaît exactement le même langage.

Les alphabets de A_n et de A_d sont identiques.
Les états de départ sont respectivement q₀ et le singleton {q₀}.
Q_d est constitué de tous les sous-ensembles de Q_n.
F_d est l’ensemble des sous-ensembles de Q_n qui contiennent au moins un élément de F_n.
Étant donné un sous ensemble S de Q_n et un symbole a ∈ Σ, on définit la fonction de transition δ_d(S,a) de la manière suivante
δ_d(S,a) =

∪

q ∈ S

δ_n(q, a).

Nous illustrons le théorème de Rabin-Scott sur quelques exemples.

Exemple 7.3 reprenons l’exemple de l’exercice 7.8. Il s’agissait de construire un automate fini non-déterministe reconnaissant les mots de l’alphabet {a,b} qui terminent par bab. L’automate suivant répond à la question.

Essayons maintenant de le déterminiser en construisant un nouvel état à partir de chaque sous ensemble d’état possible.

Remarquons que les états {1}, {2}, {3}, {0,2}, {0,3}, {1,2}, {2,3}, {0,1,2}, {1,2,3}, {0,2,3} sont inatteignables et peuvent être “retirés” de l’automate.

En pratique, lors de la conversion, on ne crée pas immédiatement tous les états de l’automate fini déterministe. Les états “utiles” sont crées quand on en a besoin en suivant la méthode de construction ci-dessous :

Q_d est initialisé à ∅ et soit E un ensemble d’états initialisé à E = {{q₀}}
Tant que E est non vide,
- choisir un élément S de E (S est donc un sous ensemble de Q_n),
- ajouter S à Q_d,
- pour tout symbole a ∈ Σ,
  - calculer l’état S′ = ∪_{q ∈ S} δ_n(q, a)
  - si S′ n’est pas déjà dans Q_d, l’ajouter à E
  - ajouter un arc sur l’automate entre S et S′ et la valuer par a

Exercice 7.12 Déterminiser l’automate de l’exercice 7.7 (long).

7.4.3 Les є transitions

Rappelons qu’є représente le mot vide. Une є transition (notée є sur l’arc d’un automate) permet de passer d’un état à l’autre d’un automate sans lire de symbole. Cette facilité permet de programmer facilement des automates complexes.

Une table de transition peut être associée à un automate contenant des є transition. La table est identique à celle utilisée pour un automate fini non-déterministe à ceci près qu’on la complète d’une colonne associée au caractère vide є.

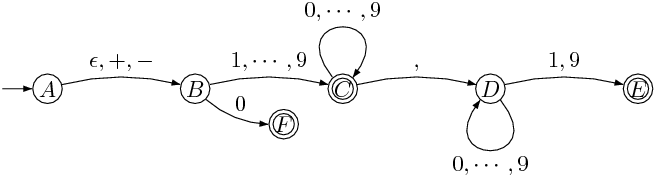
Exemple 7.4 Pour illustrer les є transitions, construisons un automate fini non déterministe qui reconnaît les nombres décimaux. Rappelons qu’un nombre décimal est un nombre réel qui est le quotient d’un entier relatif par une puissance de dix. Plus précisément, on souhaite pouvoir écrire le nombre décimal en commençant par un “+” ou un “-’, suivi d’une suite de chiffres, d’une virgule et d’une suite de chiffres. Bien entendu, le “+” ou le “-” sont optionnels, la première chaîne de chiffres ne peut pas être vide et ne commence pas par “0” (sauf si le nombre décimal est 0). La seconde chaîne ne se termine pas par “0”. Si seconde chaîne est vide, on omet la “,”.

La transition de l’état A à l’état B est régie par є,+,−. Ainsi, on peut passer de A à B soit en lisant +, soit en lisant − soit enfin en ne lisant rien.

La table de transition associée à cet automate est alors :

	є	+	−	,	0	1	2	⋯	9
→ A	{B}	{B}	{B}	∅	∅	∅	∅	⋯	∅
B	∅	∅	∅	∅	{F}	{C}	{C}	⋯	{C}
C	∅	∅	∅	{D}	{C}	∅	∅	⋯	∅
D	∅	∅	∅	∅	{D}	{D,E}	{D,E}	⋯	{D,E}
* E	∅	∅	∅	∅	∅	∅	∅	⋯	∅
* F	∅	∅	∅	∅	∅	∅	∅	⋯	∅

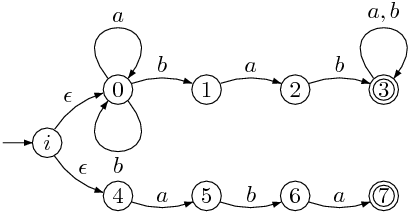
Exercice 7.13 On cherche à construire un automate qui reconnaît les mots qui se terminent par bab ou qui commencent par aba.

On sait construire un automate qui reconnaît les mots qui se terminent par bab (exercice 7.8):
il est facile de construire un automate qui reconnaît les mots qui commencent par aba.
Il suffit alors d’assembler ces automates avec une simple є transition.

L’introduction des є transition ne change pas la nature des langages reconnus par les automates. Comme pour les automates non-déterministes que l’on peut toujours déterminiser, il est toujours possible d’éliminer les є transition et d’obtenir un automate fini déterministe équivalent. Nous n’aborderons pas ici cette élimination.

7.5 Automates finis et expressions régulières

Les automates finis et les expressions régulières ont la même expressivité. En effet, le théorème d’équivalence des expressions régulières et des automates finis (Kleene) établit que Le langage accepté par un automate fini correspond à la valeur d’une expression régulière et réciproquement.

7.6 Un peu de Java

Il est aisé de représenter les automates finis sous la forme d’un programme java. Notre objectif est de

modéliser un automate fini non-déterministe (sans є transition)
et d’écrire un programme qui détermine si une chaîne de caractère est reconnue par l’automate.

Sans perte de généralité, nous allons supposer que l’alphabet est l’ensemble des caractères ASCII et que les états sont numérotés à partir de 0.

7.6.1 Modèle

Le modèle de données est alors très simple :

L’état initial de l’automate est indiqué par un entier q0.
La table de transition delta est un tableau bidimensionnel de listes d’entiers (la liste d’entier étant ici le moyen le plus simple de représenter un ensemble d’états). Ainsi delta[q][c] est la liste des états atteignables à partir de q en lisant le caractère c.
L’ensemble des états finaux est une liste d’entiers.
Enfin, le mot que l’on cherche à reconnaître est une chaîne de caractères String mot.

Soit donc en Java les deux classes List et Automate.

class Liste {
    int val;
    Liste suivant;
    Liste(int v, Liste x) {
        val = v;
        suivant = x;
    }
}

class Automate {
    int q0;           // état initial
    Liste[][] delta;  // fonction de transition
    Liste finaux;     // états finaux
    Automate(int q, Liste f, Liste[][]d) {
        q0 = q;
        delta = d;
        finaux = f;
    }
}

7.6.2 Algorithme de recherche

Nous aurons besoin de quelques fonctions classiques sur les listes

static int longueur(Liste x) {            // La longueur d'une liste
    if (x == null)
        return 0;
    else
        return 1 + longueur(x.suivant);
}
static int kieme(Liste x, int k) {       // Le k ème élément
    if (k == 1)
        return x.val;
    else
        return kieme(x.suivant, k-1);
}
static boolean estDans(Liste x, int v) { // Le test d'appartenance
    if (x == null)
        return false;
    else
        return x.val == v || estDans(x.suivant, v);
}

La fonction accepter(String mot, Automate a) qui permet de vérifier qu’un mot mot est accepté apr l’automate a appelle la fonction static boolean accepter(String mot, Automate a, int i, int q).

static boolean accepter(String mot, Automate a) {
    return accepter(mot, a, 0, a.q0);
}
static boolean accepter(String mot, Automate a, int i, int q) {
    if (i == mot.length())
        return Liste.estDans(a.finaux, q);
    else {
        boolean resultat = false;
        int c = mot.charAt(i);   // le code ASCII du caractère courant
        for (Liste nv_q = a.delta[q][c]; nv_q != null; nv_q = nv_q.suivant)
            resultat = resultat || accepter(mot, a, i+1, nv_q.val);
        return resultat;
    }
}

La fonction static boolean accepter(String mot, int i, Automate a, int q) prend, en plus de l’automate et du mot que l’on étudie, deux autres paramètres :

La position du caractère courant i dans le mot.
L’état courant q.

Elle renvoie true si et seulement si le sous-mot de mot dont on a retiré les i premiers caractères était reconnu par un automate semblable à a dont l’état initial serait q.

Remarquons que si i est le dernier caractère du mot (ce qui correspond au test if (i == mot.length())) alors il suffit de tester l’appartenance de q à a.finaux. Si ce n’est pas le cas, on va essayer d’emprunter toutes les transitions possibles. on explore ainsi tous les états nv_q.val atteignable à partir de q en lisant c. Une fois dans l’état nv_q.val, on appelle récursivement accepter.

7.6.3 Mise en œuvre sur un automate

Considérons l’automate suivant qui accepte toutes les chaînes qui se terminent par “01”.

La table associée à cet automate est alors :

	0	1
→ 0	{0,1}	{0}
1	∅	{2}
* 2	∅	∅

Pour le construire, il nous suffit de construire la table de transition.

    public static void main(String [] arg) {
        Liste[][] delta = new Liste[3][128];
        delta[0][(int)'0'] = new Liste(0, new Liste(1, null));
        delta[0][(int)'1'] = new Liste(0, null);
        delta[1][(int)'0'] = null;
        delta[1][(int)'1'] = new Liste(2, null);
        delta[2][(int)'0'] = null;
        delta[2][(int)'1'] = null;
        Automate a = new Automate(0,
                                  new Liste(2, null),
                                  delta);
        System.out.println("accepter = " + accepter(arg[0], a));
    }

Remarquons que le code ASCII du caractère ’0’ est obtenu par (int)’0’.

Exercice 7.14 Comment procéder pour coder un automate avec des є transitions ?