7 Performance
7.1 Elements of complexity analysis
Given some pattern matching expression of m patterns, algorithm I
(Section 5) is called once and U′ (previous
section) is called m times with matrix arguments of 0, …,
m−1 rows. We can roughly assimilate I with U. As regards
U′, after a first, linear phase, U is called once, if they are
no or-patterns, or as many times as there are or-pattern alternatives.
Disregarding or-patterns and (unreasonably) assuming that U is
linear in its input size, we expect a quadratic behavior in the size
of the pattern matrices, which we define as the sum of the sizes of its
patterns, and will assimilate to source file size in experiments.
Namely, for a matrix of size S with m rows,
we perform m+1 calls of U on arguments of size at most S,
where m is, at worst, of the same order of magnitude as S.
Here, we do not claim to perform a thorough complexity
analysis. Rather, we intend to define a reachable target for
the running time of a practical implementation.
As a matter of fact, even when or-patterns are not considered, the
useful clause
problem is NP-complete Sekar et al. [1992].
It is thus no surprise that algorithm U can exhibit exponential
time behavior in the size of its arguments P and q→. This
exponential behavior originates from inductive
step 2-(a) (Section 3.1): the rows of matrix P whose
first pattern is
a wildcard get copied into all specialized matrices S(ck, P), and
recursive calls on all these matrices may be performed.
The most unfavorable situation is as follows:
U(P, q→ ) is false;
all patterns in q→ are wildcards;
and the patterns in P contain mostly
wildcards and a few different constructor patterns such that
constructors collected column-wise are complete signatures.
And indeed, one can construct a series of
matchings that confirms the exponential time behavior of a
straightforward implementation of algorithm U.
Besides, randomly generated matrices also confirm that
the exponential time behavior can occur.
Such problematic random matrices test vectors of booleans and
many of their patterns are wildcards.
7.2 Safeguards
Input to the Objective Caml compiler a priori is neither nasty
nor random, it consists of programs written by human beings attempting
to solve specific problems, not to break the compiler.
If such reasonable input triggers exponential behavior, then the
compilation of useful programs may perhaps become unfeasible.
We now search for means that may prevent U from reacting exponentially to
reasonable input. We call such a mean a safeguard.
An exhaustive match is a
potentially unfavorable situation, since we here compute
U(P, (_⋯_)) = False.
Hence, we examine how human
beings write exhaustive matches.
An easy and frequent way to ensure exhaustiveness is to complete a matching
with a wildcard pattern.
Hence, we could first scan matrices searching for rows of wildcards,
and announce exhaustive match as soon as we discover one.
However, this process would not be very general.
Let us rather consider strict pattern matching and remark
that for any defined value we have _ ≼ v.
That is, for any pattern p and defined value v, we have
p ≼ v =⇒ _ ≼ v
(or _ ⋠v =⇒ p ⋠v).
Hence, if some row of some matrix P is made of wildcards,
then that row contains all the non-matching potential
of the whole matrix P.
Wildcards can also appear inside patterns, as in the following
example.
match v with (1,2) -> 1 | (1,_) -> 2
Then, for any defined value v, we have
(1,2) ≼ v =⇒ (1,_) ≼ v
(or
(1,_) ⋠v =⇒ (1,2) ⋠v).
Thus, before we compute exhaustiveness, we can delete pattern
(1,2) from the matching,
because its presence does not add non-matching values
to those values that do not match the remaining pattern (1,_).
We now consider the general case.
Definition 13
Let
p→ and
q→ be two pattern vectors.
By definition,
p→ subsumes q→ when, for all
defined value vectors
v→, we have:
q→ ≼
v→ =⇒
p→ ≼
v→.
Lemma 5
Let
P be a pattern matrix.
We further assume that there exist two rows of
P,
p→ i and
p→ j, such
that
p→ i subsumes
p→ j.
And we write
P′ for
P without
row
p→ j. Then, for any pattern vector
q→ we have:
U(
P,
q→ ) =
U(
P′,
q→ ).
Proof:
By definition of ⋠ we have:
Furthermore, by definition of
P′ ⋠
v→ and by
hypothesis “row
p→ i subsumes
p→ j”, we have:
Finally, for any defined value
v→ we have:
P′ ⋠
v→ ⇐⇒
P ⋠
v→.
□
Example 4
Let us consider the following matrix
P.
Because the constructor of pairs “
,” is alone in its
signature, pattern
(_,_) subsumes pattern _.
Namely, any (defined) value
v that possesses the type
t1 ×
t2
of a pair can be written
v = (
v1,
v2) and is thus an instance of
(_,_)3.
As a consequence, erasing any of the two rows of
P does not matter
and
we have:
| U(P, | | ) =
U( | ⎛
⎝ | | ⎞
⎠ | , | | )
=
U( | ⎛
⎝ | | ⎞
⎠ | , | | )
|
It turns out that we can decide the relation “p→ subsumes
q→” by using predicate U.
Lemma 6
Let
p→ and
q→ be two pattern vectors.
Then
p→ subsumes
q→, if and only if
U(
p→,
q→ ) does not hold.
Proof:
The property is obvious by considering the strict semantics of pattern
matching.
| U( | | , | | ) = False
⇐⇒ | ⎛
⎜
⎜
⎝ | ∀ | | , | | ≼ | | ∨ | |
⋠ | |
| ⎞
⎟
⎟
⎠ |
⇐⇒ | ⎛
⎜
⎜
⎝ | ∀ | | , | | ≼ | | =⇒ | | ≼ | |
| ⎞
⎟
⎟
⎠ |
Notice that ∀
v→ here means “for all defined values”.
□
By Lemma 5 and Lemma 6, we now have
a mean to delete rows from matrix P before we compute U.
And this mean is valid for all our semantics of pattern matching.
More precisely, we have:
| U( | | i, | | j) = False =⇒
U(P, | | ) = U(P′, | | ).
|
Where P′ is P without row number j.
In practice, before computing U(P, q→ ),
our first safeguard consists in deleting any row of P that is
subsumed by another row of P.
In the worst case,
(when no row is subsumed) this requires computing U(p→ i,
p→ j) for all pairs of (distinct) rows in P.
However, in the absence of
or-patterns, computing U(p→ i, p→ j) cannot be
exponential — since bad case 2-(a) may only occur here for constructor
signatures of size one, which, in that particular case, yields
exactly one recursive call.
We can thus approximate the cost of our first safeguard
as a quadratic number of “ordinary” pattern
operations whose cost is roughly linear in the size of input patterns
(still disregarding or-patterns).
As a conclusion, if this first safeguard saves us from exponential
computations, it is worth its price.
We now design a second, less expensive, safeguard. Two patterns are
said to be incompatible when they have no instance in common. Thus,
before computing U(P, q→ ) we can delete some row p→ i
from P, provided p→ i and q→ are incompatible
(consider strict matching). It turns out that incompatibility of
patterns can be computed as an “ordinary” pattern operation by using
the rules for computing the incompatibility of pattern and value
(see Section 4.2). Thus, we can attempt to
simplify matrix P with m rows for the price of m ordinary
patterns operations. Unfortunately, this process does not help while
checking exhaustiveness, since (_⋯_) is compatible with any
pattern vector. Furthermore, the first phase of computing U′(P,
q→ ) for checking utility in fact gets rid of rows that are
incompatible with checked row q→ (at step 1.). However, the
price of this second safeguard is low and it may be a good idea to
perform it before performing the first safeguard.
As a result, we may reduce the size of input to the first safeguard.
Of course, this makes sense because the first safeguard performs a
quadratic number of ordinary pattern operations while the second
safeguard performs a linear number of ordinary pattern operations.
In fact, example I of the following section exhibits
S3 behavior without the second safeguard, whereas, with second
safeguard enabled, it exhibits quasi-quadratic behavior.
7.3 Measures
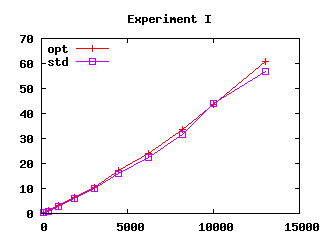
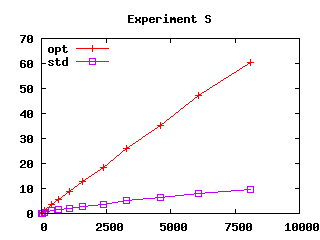
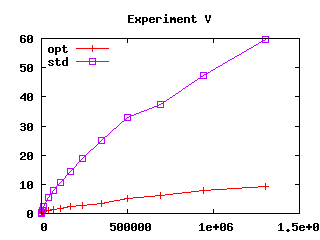
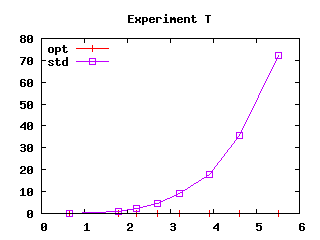
| Figure 3: Effect of safeguards in four experiments.
User CPU time (in seconds) as a function of file size squared (in
kilobytes squared) |
We performed some measures of the machine time taken by our
implementation, which is integrated in the Objective Caml
compiler.
We measure compilation time both with and without pattern-matching
diagnostics enabled. Then, a simple subtraction yields
the time taken by the detection of anomalies.
Measures apply to series of pattern-matching expressions of identical
structure and increasing size. Three of our series T,
S and V, may drive compilation of pattern matching to
decision trees into producing code of exponential size. We selected
those because algorithm U is similar to compilation of pattern
matching to decision trees. The fourth series, I, is the
matching of n constant constructors. We selected series I
because of a real example that triggered excessive compilation times
while we were implementing algorithm U. All series are defined
precisely in appendix A. In Figure 3, the
X-axis shows the size of matchings squared, (expressed as source file
size squared), while the Y-axis shows user machine
time on a Linux 1Ghz PC. We perform measures both with and without
the safeguards described in the previous section (those are named
“opt” and “std”).
Experiments S and V demonstrate that algorithm U is
more resistant to exponential behavior than simple compilation to
decision trees.
Namely, exponential behavior of compilation to decision trees
have been reported
for those examples Sestoft [1996], Maranget [1992].
Observe that algorithm U does not exhibit
exponential running time even without safeguards (written “std” in
Figure 3).
However, algorithm U is not immune from exponential behavior, as
demonstrated by experiment T. In that particular case,
safeguards prove efficient and we decided to retain them in our
implementation for that reason. Adopting safeguards incurs some
penalty, since safeguards significantly degrade performance in
experiment S. However, it should be noticed that it requires a
161 × 320 matrix to reach one minute of analysis time in
experiment S (with safeguards), whereas it takes only a 42
× 21 matrix to reach a similar time in experiment T
(without safeguards).
Finally the plots of figure 3 suggest that the running time
of pattern matching analysis with safeguards is approximatively
quadratic in input size, at least for our examples and on the studied domain.
However, notice that experiment I suggests a slightly more than
quadratic running time.
We also estimate the time taken by our algorithm
relatively to total compilation time of ordinary programs. To do so,
we measure the
running time of the compilation of some programs, with pattern
matching analysis disabled (no),
with pattern matching analysis enabled but without safeguards
(std), and with safeguards (opt).
We made some effort not to measure
irrelevant operations such as linking and the application of external
tools.
We made ten measures in each experiment and we computed geometric
means.
The compiled programs are the Objective Caml compiler itself
(ocamlc), the hevea LATEX to html translator
and another compiler (zyva).
All those programs use pattern matching significantly and are of
respectable size.
| | no | std | opt |
| ocamlc | 13.63 | 13.92 | 14.02 |
| hevea | 7.84 | 8.01 | 8.05 |
| zyva | 4.61 | 4.70 | 4.74 |
|
Those results show that the price of pattern-matching analysis remains
quite low in practice.
One might even conclude that safeguards are not very useful when it
comes to compiling “actual” programs. Still, we adopt
safeguards because they are designed to avoid exponential behavior
in some specific situations, which do not show up in the above
examples.
Our choice follows the general philosophy behind preferring
backtracking automata to decision trees: avoid exponential
behaviors as much as possible.