3 Pattern matching in join definitions
3.1 Principle
Consider the following join definition:
let A(n) | B() = P(n)
and A(n) | C() = Q(n)
;;
This defines three names A, B and C. Name A has arity one,
whereas names B and C have arity zero. Names may be synchronous
or asynchronous, depending on whether there are
reply… to…
constructs applying to them inside the guarded processes P(n)
and Q(n) or not.
According to the general join-calculus semantics, the guarded process
P(n) may be fired whenever there are some messages pending on A and
B. Similarly, Q(n) may be fired whenever there are some messages
pending on A and C. In both cases, the formal parameter n is
replaced by (or bound to in the implementation) one of the messages
pending on A.
Reactivity information is to be considered at the definition level,
since matching is indeed performed at this level. Moreover, in order
to use finite-state automata, we want this information to range on a
finite set of possible values. As far as matching is concerned and by
the linearity of patterns, only the presence or absence of messages
matters. Thus, let us call 0 the status of a name without
any message pending, and N the status of a name with at least
one message pending. Then, the status of a definition is a tuple
consisting of the statuses of the names it defines, once some
arbitrary order of these names has been adopted.
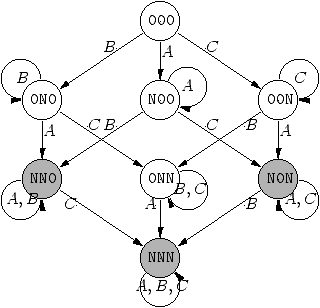
For instance, if some messages are pending on B and C, whereas
none is pending on A, then the status of the A, B, C
definition is a three-tuple written 0NN.
A matching status is defined as a status that holds enough
N, so that at least one guarded process can be fired.
Definition status evolves towards matching status as messages arrive.
This yields a first kind of “increasing” transitions. More
specifically, when a message arrives on some name, then this name
status either evolves from 0 to N or remains
N. Definition status evolves accordingly. In the A, B,
C case we get the following transitions. (In this diagram,
transitions are labeled by the name that gets a new message and
matching statuses are filled in gray.)
Definition status also evolves when matching occurs. This yields
new, “decreasing”, transitions that we call matching transitions.
According to the join-calculus semantics,
matching may occur at any moment (provided of course that
matching is possible).
As a consequence, matching transitions start from matching states and
they are unlabeled.
In the A, B, C case, they are as follows:
Observe that there may be several matching transitions starting from a
given status. This is not always a consequence of the
non-deterministic semantics of the join-calculus.
Often, ambiguity is only apparent. For instance, matching transitions
starting from NN0 lead to NN0, N00,
0N0 and 000. When such a matching occurs, two
messages are consumed (one pending on A and one pending on B)
then, depending on whether there are some messages left pending on A
and B or not, status evolves to NN0, N00,
0N0 or 000. From the implementation point of view,
this means that a little runtime testing is required once matching has
been performed. Here, we pay a price for using finite-state automata.
However, some true non-determinism is still present. Consider
status NNN for instance. Then, both guarded processes of the
A, B, C definition can now be fired. The choice of firing
either P(n) or Q(n) will result in either consuming one message
pending on A and one on B, or consuming one message pending on A
and one on C.
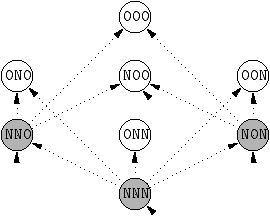
Finally, a view of join-matching compilation can be given by taking
together both kinds of transitions. This yields a non-deterministic
automaton.
Note that matching of non-linear patterns can also be compiled using automata.
For instance, if a name appears at most twice in one or more pattern,
then it status will range on 0, 1 and N.
We do not present this extension in greater detail, for simplicity, and
because we do not implement non-linear patterns.
3.2 Towards deterministic automata
For efficiency and simplicity reasons we choose to implement matching
using deterministic automata that react to message reception.
Fortunately, it is quite possible to do so. It suffices to perform
matching as soon as possible. More precisely, when a message arrives
and carries definition status into matching status, matching is
performed immediately, while definition status is adjusted to reflect
message consumption. This results in pruning the status space just
below matching statuses.
In practise, in the A, B, C case, we get the
automaton of figure 1.
Figure 1:
Automaton in the
A,
B,
C case
Observe that all transitions are now labeled and that a name labels a
transition when message reception on this name triggers that
transition. Furthermore, matching transitions that correspond to
firing P(n) or firing Q(n) are now represented differently (the
former by a dotted arrow, the latter by a dashed arrow). This
highlights the difference between false and true non-deterministic
transitions: real non-determinism is present when there are both
dotted and dashed edges with the same label starting from the same
node.
For instance, there are two B-labeled dotted transitions starting
from N00. Non-determinism is only apparent here, since
P(n) is fired in both cases and that the selected transition depends
only on whether there is at least one message left pending on A
or not after firing P(n).
By contrast, from status 0NN, the automaton may react to the
arrival of a message on A in two truly different manners, by firing
either P(n) or Q(n). This is clearly shown in figure 1 by
the A-labeled edges that start from status 0NN, some of
them being dashed and the others being dotted. A simple way to avoid
such a non-deterministic choice at run-time is to perform it at
compile-time. That is, here, we suppress either dotted or dashed
A-labeled transitions that start from 0NN.
In the rest of the paper, we take automata such as the one of
figure 1 as suitable abstractions
of join-pattern compilation output.
3.3 Automata and semantics
Both the “match as soon as possible” behavior and the deletion of
some matching transitions have a price in terms of semantics.
More precisely, some CHAM behaviors now just cannot be observed
anymore.
However,
the CHAM semantics is a non-deterministic one: an initial
configuration of the CHAM may evolve into a variety of configurations.
Furthermore, there is no fairness constraint of any kind and
no particular event is required to occur.
As an example of the consequence of the “match as soon as possible”
behavior, consider this definition:
let A() = print(1);
and B() = print(2);
and A() | B() = print(3);
;;
Then, we get the following automaton:
Status NN that is preceded by the two matching statuses
0N and N0 cannot be reached. As a consequence, the
above program will never print a 3, no matter how many messages
are sent on A and B.
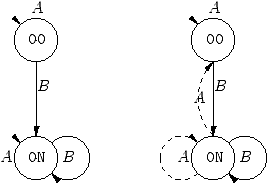
Next, to illustrate the effect of deleting ambiguous matching
transitions, consider the following definition:
let A() = print(1);
and A() | B() = print(2);
Such a definition will get compiled into one of the following
deterministic automata:
In the case of the left automaton, only 1 will ever get printed.
In the case of the right
automaton, 2 will be printed when some messages arrives on B
and then on A.
Both automata lead to correct implementations of the semantics. However
the second automata looks a better choice than the first one, since it
yields more program behaviors.