Compilation de pseudo-pascal

1  Contexte informatique

Une archive zyvaic.tar est fournie. Le compilateur complet de Pseudo-Pascal vers le code intermédiare se compile par : « make zyvaic ».

Le but de cette semaine est d'écrire l'implémentation du module Trans, de génération du code intermédiaire. Donc dès maintenant récuperez l'archive zyvaic.tar et le fichier incomplet squelette.ml, décompactez l'archive et nettez-y le fichier incomplet à sa place. 
# tar xf zyvaic.tar
# mv squelette.ml zyvaic/trans.ml
On peut alors compiler le compilateur, après reconstruction des dépendances. 
# cd zyvaic
# make depend
# make zyvaic
Les moyens de mise au point à votre disposition sont, d'une part un imprimeur du code produit (option -pc de zyvaic), et d'autre part un simulateur qui exécute le code intermédiaire (option -ic de zyvaic et comportement par défaut).

Vous pouvez exécuter tous les tests du compilateur à l'aide de la commande : « make okic ». Le succès des tests est votre « repère de réussite » (le but à atteindre).

2  Contexte pédagogique

L'énoncé contient des références aux transparents du cours et au poly, notamment au sujet des modules fournis à utiliser (frame.mli et gen.mli). Mais rien de remplace la lecture des interfaces de ces modules, qui sont commentées.

Partie I
Compilation vers le code intermédiaire

3  Expressions et instructions

Il faut écrire le code du module Trans conforme à l'interface trans.mli.
type 'a procedure = Frame.frame * 'a
type 'a program =
    { number_of_globals : int;
      main : 'a procedure;
      procedures : 'a procedure list
    }

val program : Pp.program -> Code.stm program
Rapidement ce module transforme les programmes source en code intermédiaire (interface code.mli).

Le code à écrire ressemble pas mal à celui d'un interpréteur. Il s'agit ici encore de parcourir l'arbre de syntaxe du programme tout en résolvant les liaisons de variables, selon exactement le même schéma (trois sortes de variables : fonctions, variables globales, variables locales). Pour réaliser les environnements, on utilsera cette fois le module Env fourni (interface env.mli)

On propose de procéder en deux temps en partant du squelette fourni, que je décris un peu maintenant. Commencer par ne considérer ni variables ni fonctions (mais quand même les primitives), on va donc traduire les Pp.expression en Code.exp et les Pp.instruction en Code.stm, genre :
let rec cexpr env = function
| Int i -> Const i
| Bool b -> ...

let rec cinstruction env = function
| Sequence is -> Seq (cinstruction_list env is)
| Print_int e -> Exp (Call (Frame.write_int, cexpr env e))
| ...

and cinstruction_list env is = List.map (cinstruction env) is
Autant aussi se préocuper de la structure des programmes, même si on ignore pour le moment la gestion des noms. Donc on traduira une fonction string * Pp.definition en une fonction Frame.frame * (Code.stm)procedure. Et finalement un programme Pp.program en (Code.stm)program. Genre :
let cfun env f
    (s,{arguments = args ; result = r ; local_vars = locs ; body = ins}) =
  and new_env = env in (* Pour le moment *)
  f, Seq (cinstruction_list new_env ins)

(* Note: les frames sont bidons, pour le moment *)

let cprog {global_vars = g ; definitions = defs ; Pp.main = p} =

  let main_def = (* Corps du programme -> procédure *)
    ("main",{arguments = [] ; result = None ; local_vars = [] ; body = p}) in

  let globals = [] and frames = [] (* Pour le moment *) in

  let env_init = Env.create_global globals frames in

  let funs = List.map (fun def -> cfun env_init Frame.bidon def) defs in
  let principal = cfun env_init Frame.bidon main_def in

  { number_of_globals = List.length globals ;
    main = principal ; procedures = funs }
(Il s'agit de la réalisation de la compilation des fonctions et du programme décrite dans le cours.)

Il faut dans cette première partie, essentiellement écrire les fonctions cexpr et cinstruction, dont les définitions sont plus ou moins données dans le cours. On ne se privera pas, pour des informations plus détaillées, de consulter la section du poly sur la génération de code (et de bien utiliser le module fourni Gen pour les étiquettes et les temporaires.

Le code produit n'est pas forcément exécutable par le simulateur, mais on peut toujours le regarder à l'aide de l'option -pc. On pourra ainsi compiler le programmme a.p et voir le code a.log. L'affichage utilise une notation préfixe facile à comprendre et qui résout le problème des parenthèses en en mettant partout.
Voir la solution, si besoin

4  Variables et fonctions

Dans un deuxième temps, on se préoccupe des variables. Un module donné Env réalise la gestion des environnements. L'interface env.mli est à lire avec attention.

Elle définit un constructeur de type ('a, 'b)environnement des environnements qui associe des chaînes à à des 'a et à des 'b. Soit deux catégories de liaisons, la première pour les variables et la seconde pour les fonctions. On choisira donc Frame.frame pour les fonctions et des valeurs du type
type acces = Tempo of Gen.temp | Memo of Code.expr
pour les variables. Et on aura :
  1. des temporaires frais pour les arguments et les variables locales,
  2. des addresses en mémoire pour les variables globales. La convention pour les variables globales est de les ranger à un offset déterminé à la compilation de l'addresse de base Frame.global_register.
(Voir le cours et des précisions sur le module Frame pour les frames des fonctions.)

On notera que, puisque les fonctions de Pseudo-Pascal sont toutes potentiellement mutuellement récursives, les frames doivent tous être construits avant de commencer la génération du code, voir le poly.

On notera aussi que la compilation de la primitive read (qui prend un nom de variable en argument) pose un léger problème.

On oubliera pas de compiler et de tester dès que possible, on compile par « make zyvaic » et on teste par « make okic » qui exécute tous les sources .p du sous-répertoire test.
Voir la solution, si besoin

Partie II
Après la génération de code

On s'attache maintenant à procéder à une meilleure canonisation et à l'optimisation des traces. Compte tenu des changements intégrés dans zyvaic depuis la dernière fois. Il faut commencer par bien suivre la procédure suivante.
  1. Récupérer la nouvelle archive zyvaic.tar et la solution trans.ml de l'exercice précédent.
  2. Désarchiver, mettre la solution de l'exercice précédent en place et compiler. 
    # tar xf zyvaic.tar
# mv trans.ml zyvaic
# cd zyvaic
# make depend
# make zyvaic

5  Canonisation-Linéarisation

Le code de canonisation proposé dans zyvaic est particulièrement minimal. Il produit un nombre astronomique de transferts de temporaires.

5.1  Un exemple

Commencer par vous positionner dans le répertoire zyvaic, si ce n'est déjà fait. Le source test/fib.p est ce bête programme :
program
  var n : integer;

function fib (n : integer) : integer;
begin
   if n <= 1 then
      fib := 1
   else
      fib := fib (n-1) + fib(n-2)
end ;

begin
   read (n);
   writeln (fib (n))
end.
Par ./zyvaic -pc test/fib.p on obtient entre autre ceci. 
*** Code généré ***
function fib
args =  $t106
result = $t105
  Seq
    Seq
      Cjump L12 L13 (<= $t106 1)
    L13:
      (set $t105 (+ (call fib (- $t106 1)) (call fib (- $t106 2))))
      Jump L14
    L12:
      (set $t105 1)
    L14:

*** Code canonique et linéarisé ***
  (set $t108 $t106)
  (set $t107 1)
  Cjump L12 L13 (<= $t108 $t107)
L13:
  (set $t115 $t106)
  (set $t114 1)
  (set $t116 (- $t115 $t114))
  (set $t117 (call fib $t116))
  (set $t118 $t117)
  (set $t110 $t106)
  (set $t109 2)
  (set $t111 (- $t110 $t109))
  (set $t112 (call fib $t111))
  (set $t113 $t112)
  (set $t105 (+ $t118 $t113))
  Jump L14
L12:
  (set $t105 1)
L14:
Le code « canonique et linéarisé » est très mauvais. On remarque en particulier l'utilisation clairement excessive des temporaires dès qu'il faut calculer un peu, vers l'étiquette L13. En fait on préférerait un code de ce genre, également canonique (pas d'appels de fonction dans les expressions, ordre gauche-droite respecté) : 
*** Code canonique et linéarisé ***
  Cjump L12 L13 (<= $t106 1)
L13:
  (set $t110 (call fib (- $t106 1)))
  (set $t109 (call fib (- $t106 2)))
  (set $t107 (+ $t110 $t109))
  Jump L14
L12:
  (set $t105 1)
L14:

5.2  Allez-y

Le code de canonisation de zyvaic est dans l'implémentation canon.ml. Les fonctions qui itèrent la procédure de canonisation rewrite_exp et rewrite_stm ne sont pas en cause, elle réalisent simplement les réécritures définies dans le poly.

La coupable est la fonction commute (au début de canon.ml). Elle est assez prudente :
(* test de commutation vraiment simple *)
let commute c s =  false
Par conséquent, la règle améliorée de canonisation ne s'applique jamais.

Remédiez à ce problème en écrivant un bon test de commutation. La démarche suggérée est la suivante. On se gardera bien d'oublier que s et c ne sont pas n'importe quel code ou n'importe quelle expression, afin de simplifier le codage. Plus précisément le code s et l'expression c sont produits par les règles de canonisation. Ainsi, par exemple, c ne peut pas contenir d'appel de fonction et s est encore plus contraint.

Le moyen de test privilégié est « make okic », qui dénoncera très probablement toute erreur. Notez que l'on peut voir le code intermédiaire dans divers états en passant l'option « -pc » à zyvaic.
Voir la solution, si besoin

6  Optimisation des traces

Les traces de zyvaic ne sont pas optimisées, le code du module Linear (bien mal nommé) ne fait rien d'autre que de transformer les instructions de test bi-étiquette en instructions de test standard.

Compte tenu du temps qui nous est imparti, nous allons nous limiter à la genération du graphe de flot, que nous allons dessiner à l'écran à l'aide d'un programme idoine disponible sur vos stations.

6.1  Un exemple

L'exercice précédent étant résolu, le code canonisé-linéarisé de la fonction fib est donc le suivant : 
*** Code canonique et linéarisé ***
fib:
  Cjump L12 L13 (<= $t106 1)
L13:
  (set $t110 (call fib (- $t106 1)))
  (set $t109 (call fib (- $t106 2)))
  (set $t107 (+ $t110 $t109))
  Jump L14
L12:
  (set $t105 1)
L14:
  (jump fib_end)
Le code commence par une étiquette fib et se termine par un saut vers l'étiquette fib_end qui sont ajoutés ci-dessus. C'est normalement implicite, mais j'ai explicité.

Le premier bloc de base commence en fib et peut se terminer par un transfert du contrôle vers L12 ou L13 Le bloc d'étiquette L12 se termine nécessairement par un transfert du contrôle au bloc L14, etc. Les aventures du contrôle au cours des exécution possibles d'un programme sont avantageusement exprimées par un graphe de flot dont les sommets sont les blocs de base et les arcs traduisent les transferts potentiels de la fin d'un bloc au début d'un autre. 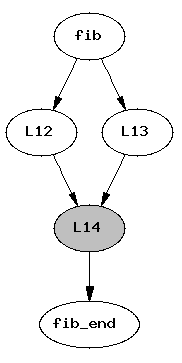Voici le graphe de flot du code de fib.
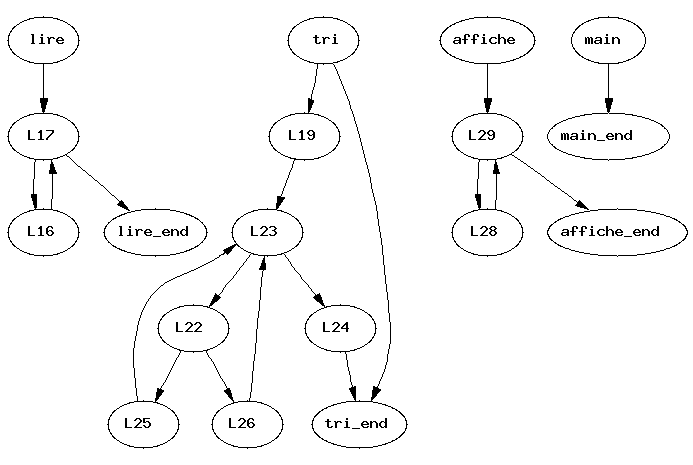
Au passage le bloc L14 est vide, c'est à dire qu'il ne contient pas d'intruction et se termine par un saut inconditionnel. Cette condition est indiquée par un sommet grisé dans le graphe de flot. L'analyse du graphe de flot permet par exemple l'élimination systématique des blocs vides (c'est à dire si on y pense des sauts vers des sauts inconditionels).

6.2  Allez-y

On va se contenter de produire une liste des blocs de base, d'afficher le graphe correspondant, puis de retransformer la liste de blocs en code. En pratique, il faut modifier le fichier linear.ml (bien mal nommé) de zyvaic. Pour une fonction (de Pseudo-Pascal) donnée c'est la fonction opt_trace (de Caml, vers la ligne 100 de linear.ml) qui fait ce petit travail :
(* Optimisation du contrôle de f (dont le code est c) *)
let opt_trace f c =
  let blocks = code_to_blocks f c in
  if !Misc.dump_flowgraph then print_flow_graph blocks;
  peephole f (blocks_to_code blocks)

(* Idem, mais inoffensif *)
let opt_trace f c = peephole f c
On commencera par supprimer la fonction opt_trace inoffensive, afin d'activer celle qui travaille vraiment. On recompile (make zyvaic) on essaie (./zyvaic -pc test/fib.p). Ça plante, c'est normal, car il y a deux fonctions à écrire. Enfin, nous y voilà ! Donc, il faut écrire code_to_blocks et blocks_to_code (chercher les raise PasFini). Les types sont les suivants :
val code_to_blocks : Frame.frame -> Code.stm list -> basic_block list
val blocks_to_code : basic_block list -> Code.stm list
Le type des basic_bloc des blocs de base mérite une petite explication.
type basic_block = {enter:Gen.label ; mutable succ:stm ; body:stm list}
C'est un type d'enregistrement. Par convention et pour une fonction donnée représentée par le frame f la première étiquette du premier bloc est Frame.frame_name f et les sauts vers l'étiquette Frame.frame_return f représentent la fin de l'exécution du corps de la fonction.

Quelques conseils (inutiles sans doute...).
  1. Commencer par écrire code_to_blocks. Un fois amorcée la création d'un bloc, on cherche sa fin en un parcours de la liste des instructions, si on trouve...
    1. La définition d'une étiquette Label lab. Alors le bloc en cours de construction est terminé (son champ succ est Jump lab). Un nouveau bloc étiqueté lab commence.
    2. Un saut quel qu'il soit, le bloc en cours se termine par ce saut. L'instruction qui suit est forcément une étiquette commençant un nouveau bloc.
    3. Plus rien (fin de la liste des instructions). Le bloc en cours se termine par un saut vers Frame.frame_return f.
    4. N'importe quelle autre instruction, alors cette instruction est à ajouter en fin de bloc et il faut continuer à chercher la fin du bloc en cours.
  2. Finir par blocks_to_code, assez facile au fond (mettre le code des blocs bout-à-bout).

6.3  Moyens de test

Outre l'habituelle option -pc vous pouvez, dès que code_to_blocks est suffisament avancée, visualiser les graphes de flot. 
# ./zyvaic -pg test/fib.p | dot -Tps | kghostview -
Muni de sa nouvelle option -pg, zyvaic envoie une représentation du graphe de flot sur sa sortie standard. La construction de tuyau (pipe, noté « | ») connecte cette sortie à l'entrée standard de la commande suivant dot qui ici (option -Tps) transforme la représentation du graphe en un dessin en Postscript, visualisable par kghostview après un second tuyau. Ouf !

Plus simple encore (mais moins instructif), utiliser le script équivalent fourni. 
# ./show_flow_graph test/fib.p
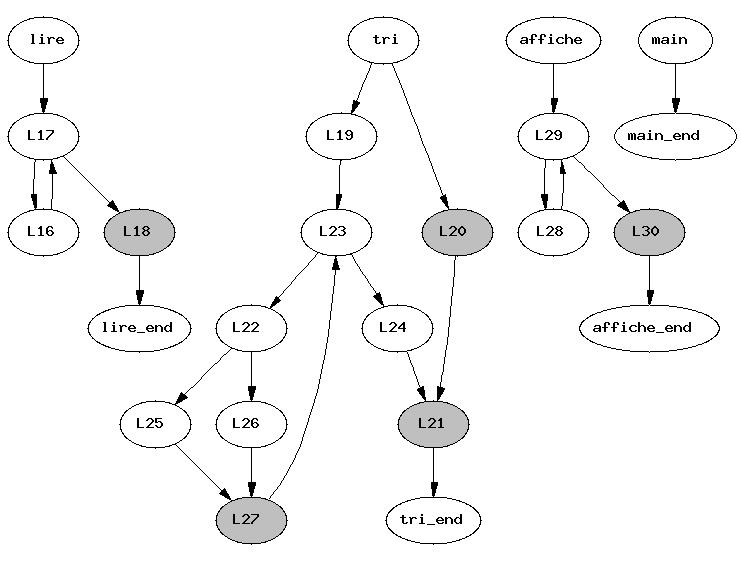
Le défi est de produire, par ./show_flow_graph test/quick.p, le magnifique graphe de flot suivant.
D'ailleurs simplifiable comme suit (mais c'est une autre histoire).

Voir la solution, si besoin

Ce document a été traduit de LATEX par HEVEA.