TD-7, arbres de recherche

Ce document est disponible à l'URL http://www.enseignement.polytechnique.fr/profs/informatique/Luc.Maranget/TC/X.97/TD-7/enonce.html

Programmes Prenom.Nom.c à déposer par ftp sur poly en /users/profs/maranget/TD-7.

1 Statistique des prénoms

On se donne une liste de prénoms sous la forme d'un tableau de chaînes. Par exemple :

char *profs[] = {
  "Francois", "Bruno", "Patrice", "Jean",   "Francois", "Robert",
  "Francois", "Jean",   "Francois", "Didier",  "Didier", "Bruno",
  "Jean", "Francois", "Jean"
};

Ou mieux encore la liste des prénoms de la promo, que vous trouverez en promo.txt. On demande de produire une nouvelle liste de prénoms, où chaque prénom n'apparaît qu'une fois et est suivi de son nombre d'occurrences dans la liste initiale.

1.1 Arbre de comptage des mots

On compte les prénoms en construisant un arbre un arbre binaire de recherche dont chaque noeud contient un prénom et un compte. Voici la déclaration des cellules d'un tel arbre :

typedef struct cell {
  char *mot;
  int compte;
  struct cell *filsg,*filsd;
} *Tree;

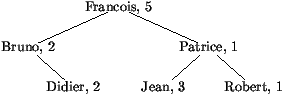
Notre arbre binaire de recherche sera ordonné selon l'ordre lexicographique (du dictionnaire) des prénoms. C'est à dire que tous les prénoms contenus dans un sous-arbre gauche (resp. droite) d'un noeud donné sont plus petits (resp. plus grands) que le prénom contenu dans ce noeud. Voici un exemple d'un tel arbre :

L'arbre de comptage sera construit en un parcours de la liste initiale des prénoms. L'examen de chaque prénom devra entraîner soit l'augmentation d'un compte (si le prénom examiné est déjà dans l'arbre), soit la création d'un nouveau noeud.

Voici deux points de programmation C :

Pour parcourir un tableau initialisé sans donner de taille, on utilise une boucle :
```
  for (i=0 ; i < sizeof(profs)/sizeof(profs[0]) ; i++) {
    ...
  }
```

On comparera les prénoms avec la fonction de bibliothèque strcmp dont voici la documentation :

SYNOPSIS
       #include <string.h>

       int strcmp(const char *s1, const char *s2);

DESCRIPTION
       The strcmp() function compares the two strings s1 and s2.  It
       returns an integer less than, equal to, or greater than zero if
       s1 is found, respectively, to be less than, to match, or be
       greater than s2.

1.2 Affichage des résultats

Programmer le parcours d'arbre qui permet d'afficher la liste des prénoms suivis de leur compte selon l'ordre alphabétique des prénoms. Dans l'exemple donné, on doit avoir :

Bruno : 2
Didier : 2
Francois : 5
Jean : 3
Patrice : 1
Robert : 1

1.3 Affichage des résultats selon les comptes

On veut obtenir un meilleur affichage des résultats : on veut que les prénoms les plus fréquents apparaissent en premier, les prénoms de même fréquence apparaissant selon l'ordre lexicographique :

Francois : 5
Jean : 3
Bruno : 2
Didier : 2
Patrice : 1
Robert : 1

Cela revient à trier les couples (prénom, compte) selon un nouveau critère. Compte tenu du code que vous avez déjà écrit, une technique assez simple est de produire un nouvel arbre de recherche ordonné selon ce critère, arbre qui sera ensuite affiché à l'aide de la fonction de la sous-question précédente.

La solution de cet exercice apparaîtra à l'URL prenoms.txt.

2 Il vous reste du temps

Cet exercice est un peu long, mais il introduit de nouvelles notions de programmations assez utiles. Afin de vous éviter de trop taper de texte, vous pourez partir d'un squelette de programme disponible en skel.txt.

2.1 Nouveaux types

C permet de définir des types enum, analogues aux types énumérés de Pascal :

typedef enum {Pique, Trefle, Coeur, Carreau} Couleur;

Cette déclaration définit un nouveau type Couleur, qui contient quatre valeurs. Une variable du type Couleur peut seulement être affectée ou comparée.

Une autre sorte de type union est analogue aux types variant de Pascal.

typedef union {
  int val;
  char *name;
} IntOrString;

Une variable v de type IntOrString contient, soit un entier (à accéder par v.val), soit une chaîne (à acceder par v.name). Il est de la responsabilité du programmeur de lire des entiers comme des entiers et des chaînes comme des chaînes, le compilateur ne fera rien pour l'y forcer.

C'est pourquoi, on utilise généralement une combinaison des types record, enum et union pour garantir une certaine cohérence. Si l'on veut un objet qui puisse contenir une chaîne ou un entier, on écrira plutôt :

typedef enum {Int, String} Nature;

typedef union {
  int val;
  char *name;
} Contenu;

typedef struct {
  Nature nature;
  Contenu contenu;
} IntOrString;

On peut maintenant imprimer un objet de type IntOrString par la fonction suivante :

void affiche(IntOrString x);
{
  if (x.nature == Int)
   printf("%d",x.contenu.val);
  if (x.nature == String)
   printf("%s",x.contenu.name);
}

2.2 Expressions aritmétiques

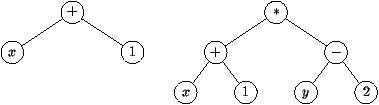
Si l'on veut manipuler des expressions arithmétiques, telles que x+1 ou (x+1) * (y-2). On est rapidement amené à les représenter par des arbres :

Les noeuds d'un arbre d'expressions sont de trois sortes, des feuilles qui sont soit un entier, soit une variable ; et des noeuds internes qui contiennent un opérateur à appliquer aux deux sous-arbres gauche et droit. On représente donc ici les cellules d'arbre par les déclarations de type suivantes :

typedef enum {Var, Num, Op} Nature;

typedef union {
  char name;
  int val;
  struct op {
      char name;
      struct tcell *gauche,*droite;
    } op;
} Contenu;

typedef struct tcell {
  Nature nature;
  Contenu contenu;
} *Tree;

Pour pouvoir s'en sortir on introduit trois fonctions de construction des noeuds, une par sorte de noeud. Par exemple, voici new_var, fonction de construction des feuilles qui sont des variables :

Tree new_var(char name)
{
  Tree r;
  
  r = (Tree)malloc(sizeof(struct tcell));
  if (r == NULL)  {fprintf(stderr,"Plus de memoire !\n") ; exit(-1)};
  r->nature = Var;
  r->contenu.name = name;
  return r;
}

Il vous est demandé d'écrire les deux autres constructeurs, new_num et new_op, ainsi qu'une fonction d'affichage des arbres (un parcours infixe produit le résultat le plus clair ici).

2.3 Derivatrice HP

Modifier la calculette HP du TD-5, afin qu'elle construise des arbres qui représentent les opérations demandées. (La calculette a donc maintenant une pile d'arbres au lieu d'une pile d'entiers). Par exemple, le programme "x1+y2-*" devra produire :

    []
x : [x]
1 : [1, x]
+ : [(x+1)]
 ...
* : [((x+1)*(y-2))]

(N.B. Les arbres sont affichés sous forme infixe.)

Dans un deuxième temps ajouter une opération de dérivations à la calculette. Cette opération pope une variable du sommet de pile puis derive l'expression en sommet de pile selon cette variable, on aura donc par exemple :

x : [x, ((x+1)*(y-2))]
d : [(((1+0)*(y-2))+((x+1)*(0-0)))]

À l'intérieur de votre programme, la fonction de dérivation prend un arbre en argument et renvoie un nouvel arbre, elle suit les règles élémentaires de dérivation de sommes, produits, etc et s'invoque récursivement.

Évidemment, l'expression dérivée demande à être un peu simplifiée...Mais la technique mise en oeuvre dans cet exercice est extrêmement générale. Une solution de cet exercice apparaîtra en deriv.txt.

Ce document a été traduit de L^AT_EX par H^EV^EA.