TD-10, encore les graphes
Programmes Prenom.Nom.c à déposer par ftp sur poly en /users/profs/maranget/TD-10.
1 Sortir vite fait d'un labyrinthe
Un petit retour sur les parcours de graphes s'impose. Pour changer, on
cherchera cette fois à trouver le chemin le plus court de l'entrée
vers la sortie.
Il faut cette fois amorcer un parcours du graphe en largeur
d'abord. Classiquement on utilise la structure de file
pour ce parcours.
La file étant une structure de données FIFO, pour First In
First Out, c'est à dire que les données sont défilées dans l'ordre de leur
enfilage.
La solution se décompose naturellement en deux sous-parties :
-
Programmation des files.
- Programmation du parcours.
Pour vous initier à la programmation en binôme, je vous propose de
vous regrouper par deux et de vous répartir le travail, l'un
programmera les files (dans un fichier file.c) et l'autre le
parcours (dans un fichier laby.c).
Pour vous entendre, il faut d'abord définir en commun un fichier
d'interface file.h qui contiendra le type des files et les
déclarations des fonctions de base sur les files.
Vous pouvez par exemple choisir le fichier file.h suivant :
/***********/
/* Files */
/***********/
typedef struct /* cellules de files */
{
Sommet me;
List to_me;
} FCell;
#define FMAX 32 /* taille maximum des files */
typedef struct { /* type des files */
int debut, fin;
FCell elem[FMAX];
} File;
void initialiser(File *f);
int est_vide(File *f);
FCell defiler(File *f);
void enfiler(File *f,Sommet s,List to_me);
Ici, un élément de file (de type FCell) comprend un sommet
(champ me) et un chemin vers ce sommet à partir de l'entrée
(champ to_me).
La file est une structure de données essentiellement définie par deux
opérations enfiler et défiler.
Par définition de la file, les éléments, sont défilés exactement dans
l'ordre de leur enfilage.
Outre les fonctions enfiler et defiler, le module des
files fournit deux autres primitives, initialiser et
est_vide.
Étant donné une file f, l'appel initialiser(&f)
initialise f en une file vide.
L'appel est_vide(&f) teste la vacuité de la file f.
Vous devez également vous entendre pour échanger des fichiers. Le
programmeur des files produisant un fichier file.c qu'il
donnera au programmeur du parcours pour qu'il l'intègre dans son
projet. Le plus simple est d'utiliser des disquettes, sinon, il faudra
passer par le réseau.
1.1 Les files
Cette section concerne le programmeur des files.
Le fichier file.h fourni suggère une implémentation des files
par un tableau de FCell.
La file est donc un tableau d'éléments, plus deux indices dans ce
tableau. L'indice debut indique la position où trouver le
prochain élément à défiler, tandis que l'indice fin indique la
position où ranger le prochain élément enfilé. De sorte que, dans une
situation simple, on peut représenter la file par un dessin :
Dans la situation simple ci-dessus décrite, l'enfilage d'un nouvel
élément produira la file suivante :
Le défilage conséquent d'un élément produira la file suivante :
Il vous reste à anticiper les situations compliquées en traitant les
cas où les indices debut et fin débordent du tableau des
éléments. Un nouvel enfilage, par exemple, devrait vous
amener à la situation suivante :
1.2 Parcours en largeur d'abord
Cette section concerne le programmeur du parcours.
Outre ce programme, vous avez la responsabilité
de l'intégration finale du produit. C'est à dire que c'est votre
programme laby.c qui contient la fonction main.
Plus précisément :
-
Vous êtes responsable des entrées-sorties
sur les labyrinthes qui sont définies et programmées dans les fichiers
labyio.h et labyio.c. Deux exemples de labyrinthes,
un petit et un grand étant disponibles.
- Vous avez également la responsabilité du projet
laby.ide
qui produira l'exécutable final laby.exe.
Si vous avez des trous de mémoire, vous pouvez
vous reporter à l'énoncé de la semaine dernière.
La file permet une programmation assez simple du parcours, il
suffit à chaque étape de défiler un sommet, puis,
d'enfiler ses voisins immédiats. Autrement dit, un parcours en largeur
d'abord générique est décrit par l'algorithme suivant :
tant que f est non-vide
e = defiler(f) ;
traiter(e) ;
enfiler tous les voisins du sommet contenu dans e
Au départ, on enfile l'entrée. Le parcours défilera l'entrée puis
enfilera ses voisins. L'étape suivante du parcours défilera donc un
voisin de l'entrée pour enfiler ses voisins. Par la propriété de file,
on a donc la certitude
que ces voisins de voisins de l'entrée ne seront défilés qu'une fois
traités tous les voisins de l'entrée.
Plus généralement, la structure de file garantit que la file (prise
dans l'ordre de défilage) se
compose d'une série éventuellement vide de sommets situés à la
distance d de l'entrée, suivie d'une série éventuellement vide de
voisins de ces sommets distants de d+1 de l'entrée.
On en déduit facilement que les sommets sont traités par éloignement
croissant de l'entrée.
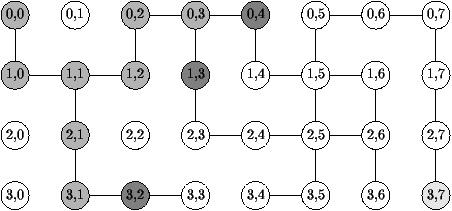
Pour vous fixer les idées voici les sommets parcourus (en gris clair)
et ceux qui sont dans la file (en gris foncé), dans le cas du petit
labyrinthe, alors que la file est á (3,2) ; (0,4) ;
(1,3)ñ. Le sommet
(3,2) est distant de 5 de l'entrée, tandis que les sommets (0,4)
et (1,3) sont les voisins du sommet (0,3) qui vient juste d'être traité.
Il vous reste à faire attention à ne pas traiter deux fois le même
sommet et à calculer correctement le champ to_me des éléments
de file, qui est un chemin le plus court de l'entrée vers le sommet
me stocké dans un élément de file donné.
Un fois trouvée le chemin sol vers la sortie du labyrinthe
laby, vous l'afficherez comme la semaine dernière par :
print_laby(stdout,laby,sol)
2 Il vous reste du temps
Écrire un programme qui trouve tous les chemins de l'entrée vers
la sortie d'un labyrinthe. Un chemin est ici défini comme ne
comportant pas de cycle. Dans le cas du petit labyrinthe :
+-+-+-+-+-+-+-+-+
|I| | | |
+ +-+ + + + +-+ +
| | | | |
+-+ +-+ +-+ + + +
| | | | | |
+-+ +-+-+-+ + + +
| | | | |O|
+-+-+-+-+-+-+-+-+
On a les solutions :
+-+-+-+-+-+-+-+-+ +-+-+-+-+-+-+-+-+ +-+-+-+-+-+-+-+-+
|I| |XXXXX|XXXXX| |I| |XXX |XXXXX| |I| |XXX |XXXXX|
+X+-+X+ +X+X+-+X+ +X+-+X+X+ +X+-+X+ +X+-+X+X+ +X+-+X+
|XXXXX| |XXX |X| |XXXXX|X| X |X| |XXXXX|X| XXX|X|
+-+ +-+ +-+ + +X+ +-+ +-+X+-+X+ +X+ +-+ +-+X+-+ +X+X+
| | | | |X| | | | |XXXXX |X| | | | |XXXXXXX|X|
+-+ +-+-+-+ + +X+ +-+ +-+-+-+ + +X+ +-+ +-+-+-+ + +X+
| | | | |O| | | | | |O| | | | | |O|
+-+-+-+-+-+-+-+-+ +-+-+-+-+-+-+-+-+ +-+-+-+-+-+-+-+-+
Il y a 3 solutions
Ce document a été traduit de LATEX par
HEVEA.