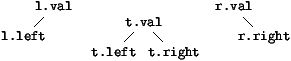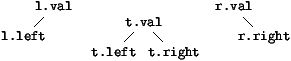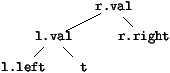Solutions du TD-6, Arbres de recherche
Voici la classe Arbre (qui était fournie), ainsi qu'une
classe Set solution.
Les méthodes cardinal, mem et add sont des
classiques.
La méthode subset est un exemple intéressant de récursion sur
les arbres binaires qui ne dépasse pas le cadre du cours.
Voici la classe ArbrePlus (qui était fournie), ainsi qu'une
classe SetPlus solution.
La méthode main qui était fourni constitue un exemple de
genre de tests que l'on peut faire passer à un programme pour se
persuader qu'il fonctionne correctement. Les tests ne remplacent pas
un preuve, même rapide du programme, mais signalent les bugs.
Pour être utliles les tests doivent être suffisamment variés et
comprendre des cas limites,
comme les ensembles vides ou l'inclusion d'un ensemble dans lui même.
Lorsque l'on développe un (gros) programme, on garde les entrées qui ont
révélé des bugs et on les redonne au programme à chaque modification
importante.
Remarquez que add est la seule méthode qui change vraiment.
Un exercice de programmation objet intéressant serait d'exprimer
ArbrePlus comme une sous-classe de Arbre et
SetPlus comme une sous-classe de Set. C'est moins
immédiat qu'il n'y paraît et ça ne sert sans doute pas à préparer le
contrôle.
2.1 Sur remove
Il s'agit donc d'écrire la methode de fusion merge sous les
conditions de l'énoncé.
En effet, une fois cette méthode écrite, on écrira remove
ainsi.
static ArbrePlus remove (int x, ArbrePlus a) {
if (a == null)
return null ;
if (x < a.val)
return balance (remove (x, a.left), a.val, a.right) ;
else if (x > a.val)
return balance (a.left, a.val, remove (x, a.right)) ;
else /* cas casse-pieds */
return merge (a.left, a.right) ;
}
On notera,
-
Que les hauteurs des arbres a.left,
et a.right diffèrent au plus de un.
(Hypothèse d'équilibrage de a).
- Sous l'hypothèse de correction de merge,
on a alors que merge (a.left, a.right) est un arbre
de hauteur celle de a ou celle de a moins un.
- Dès lors, remove renvoie bien un arbre equilibré,
(et même un arbre de la même hauteur que a, ou cette hauteur
moins un),
grâce au lemme que balance(l,x,r) renvoie un arbre de la même
hauteur que l'arbre new ArbrePlus(l, x, r), ou cette hauteur
moins un.
Une version plus précise du lemme des hauteurs à l'équilibrage est
que l'arbre équilibré a la hauteur du sous-abre le plus profond ou
cette hauteur plus un.
Reste à écrire merge...
private static ArbrePlus merge (ArbrePlus l, ArbrePlus r) {
On commence par étudier quelques cas dissymétriques.
Supposons donc que la hauteur de l soit inférieure ou égale à celle de
r.left
(noté h(l) <= h(r.left), qui implique
h(l) < h(r)).
Alors, par l'hypothèse
h(r) - h(l) <= 1,
il vient en fait h(r.left) = h(l).
Donc on peut appliquer l'induction et il vient
h(merge(l,r.left)) = h(r.left) ou
h(merge(l,r.left)) = h(r.left)+1.
Soit ensuite, par hypothèse d'équilibrage de r,
les hauteurs de merge(l,r.left) et de r.right
diffèrent au plus de deux.
Donc, on peut appliquer
balance à ces sous-arbres et le résultat sera
un arbre dont la hauteur est h(r) ou h(r)+1,
par le lemme des hauteurs à l'équilibrage.
Soit, en considérant aussi le cas symétrique, le code suivant :
if (ArbrePlus.hauteur(l) <= ArbrePlus.hauteur(r.left))
return balance (merge (l, r.left), r.val, r.right) ;
else if (ArbrePlus.hauteur(r) <= ArbrePlus.hauteur(l.right))
return balance (l.left, l.val, merge (l.right, r)) ;
Par ailleurs, la hauteur de l'arbre rendu en résultat étant
h(r) ou h(r)+1 et l'arbre r étant, par
hypothèse, plus profond que l on assure l'induction dans ce cas.
On remarque alors que les cas de franc déséquilibre (de deux) entre
l.right et r.left, h(l.left) = h,
h(l.right) = h-1, h(r.left) = h+1,
et les cas symétriques, sont traités. On peut
donc légitimement appeler merge récursivement sur
l.right et r.left :
else {
ArbrePlus t = merge(l.right, r.left) ;
Il reste à mélanger proprement t et ce qui reste des arbres
l et r.
À savoir il faut regrouper
En un arbre équilibré satisfaisant à l'hypothèse d'induction
(dont la hauteur est celle du plus profond de l et de
r, ou cette hauteur plus un).
Il y a pour ce faire deux façons de procéder, inspirées des
équilibrages normaux, la première reprend l'idée des rotations doubles
en posant :
La seconde, consiste à poser:
(Il y a bien évidemment une autre possibilité du même ordre, mais
qui penche à droite)
Commençons par supposer h(l) = h+1 et
h(r) = h+2 (autrement dit, étant donné les conditions sur
les arguments de la fusion h(l) < h(r)).
On discute ensuite selon les hauteurs des quatres sous arbres
l.left, l.right, r.left et
r.right.
Compte tenu des cas précédent, les hauteurs des sous-arbres de
r son fixées (h(r.left) ne peut pas être h+1)
et il n'y a que trois cas.
-
Cas h, h, h h+1. Dès lors, par induction h(t)
est h ou h+1.
Dans les deux cas le sous-arbre de gauche de la seconde construction est équilibré,
sa hauteur est h+1 dans le premier cas et h+2 dans le second.
Soit l'arbre final est équilibré et sa hauteur est h+2 ou h+3.
- Cas h, h-1, h, h+1. Ce cas est en tout point semblable
au précédent, le h-1 en premier argument de l'appel récursif de
merge n'ayant pas d'influence sur la hauteur de l'arbre produit.
- Cas h-1, h, h, h+1.
Dès lors, c'est encore la seconde construction qui s'applique.
Si r est de hauteur h, le sous-arbre de gauche est
équilibré de hauteur h+1, l'arbre final est équilibré de hauteur
h+2.
Si r est de hauteur h+1, le sous-arbre gauche n'est pas
équilibré, mais par un appel à balance on pourra le
transformer en un arbre équilibré de hauteur h+1 ou h+2.
Soit l'arbre final est équilibré de hauteur h+2 ou h+3.
Bref on aura le code :
if (ArbrePlus.hauteur(l) < ArbrePlus.hauteur(r))
return new ArbrePlus (balance (l.left, l.val, t), r.val, r.right) ;
else if (ArbrePlus.hauteur(l) > ArbrePlus.hauteur(r))
return new ArbrePlus (l.left, l.val, balance (t, r.val, r.right)) ;
On note au passage que l'équilibrage (appel à balance) n'est
éventuellement utile que pour le sous-arbre.
Réglons ensuite le cas où t est vide
dans le cas des hauteurs égales pour l et r, c'est
un cas particulier, (cette hauteur étant un ou deux).
On aura ici encore recourt à la seconde construction.
else { // ArbrePlus.hauteur(l) == ArbrePlus.hauteur(r)
if (t == null) {
if (Math.random() < 0.5) // Au hasard...
return new ArbrePlus (l.left, l.val, r) ;
else
return new ArbrePlus (l, r.val, r.right) ;
Reste donc à examiner le cas h(l) = h(r) = h+1.
On procède encore par sous-cas sur les hauteurs des sous-arbres
de l et r il y en a cette fois beaucoup plus de cas
(il y en a neuf).
-
h, h, h, h. La première construction est équilibrée et
de hauteur h+2,
sauf dans le cas où un des sous-arbres t.left ou
t.right est de hauteur h-2 (ce qui est possible quand
h(t) est h).
Il suffira alors d'équilibrer ce sous-arbre qui sera de hauteur h+1
ou h, tandis que l'autre fils de t sera alors
nécessairement équilibré et de hauteur h+1. Soit finalement un
arbre équilibré de hauteur h+2.
- Cas h-1, h, h, h.
Le sous-arbre gauche de la construction est toujours équilibré.
En revanche celui de droite peut être déséquilibré dans le
cas h(t) = h, h(t.right) = h-1,
h(t.left) = h-2.
Dans ce cas le sous-arbre gauche de la construction est de hauteur h.
Un équilibrage du sous-arbre droit donnera un sous-arbre de hauteur
h ou h+1 et le sous-arbre final est équilibré de hauteur h+1 ou
h+2.
Dans tous les autres cas les deux sous-arbres sont équibrés
et leur hauteurs possibles sont h et h+1, ou h+1 et h+1, soit
un arbre final de hauteur h+2.
- Cas h, h-1, h, h. Ce cas est semblable
au cas 1.
- Cas h, h, h-1, h. Cas symétrique de 3.
- Cas h-1, h, h-1, h. Cas semblable à 2.
- Cas h, h-1, h-1, h. Méchant cas.
Le cas, h(t) = h-1+1 = h ne pose aucun problème la première construction
étant équilibrée d'entrée de jeu ou justiciable d'un équilibrage qui
portera la hauteur du sous-arbre concerné à h ou h+1.
Malheureusement, cette solution n'est plus applicable au cas
h(t) = h-1 avec par exemple h(t.left) = h-3.
On se tourne alors vers la seconde solution qui elle est équibrée
d'entrée de jeu.
- Cas h, h, h, h-1. Cas symétrique de 2.
- Cas h-1, h, h, h-1. Ce cas n'est pas si méchant qu'il en
a l'air.
En effet, dans le cas h(t) = h la deuxième solution donne
directement un arbre équilibré de hauteur h+1.
Le cas h(t) = h+1 y conduit aussi, l'arbre final étant
cette fois de hauteur h+2.
- Cas h, h-1, h, h-1. Ce cas est symétrique de 5.
La programmation est bien plus simple que toute cette analyse.
Il suffit de détecter le méchant cas, puis d'appliquer la première
construction :
} else { // t != null
int h = ArbrePlus.hauteur(l.left) ;
if (h == ArbrePlus.hauteur(r.right)) {
if (ArbrePlus.hauteur(t.left) < h-2)
return new ArbrePlus
(new ArbrePlus (l.left, l.val, t), r.val, r.right) ;
if (ArbrePlus.hauteur(t.right) < h-2)
return new ArbrePlus
(l.left, l.val, new ArbrePlus (t, r.val, r.right));
}
return
new ArbrePlus
(balance (l.left, l.val, t.left),
t.val,
balance (t.right, r.val, r.right)) ;
}
}
}
J'offre une récompense à l'élève qui me montrera que mon raisonnement
est faux. Et je reconnais qu'il n'est pas possible de fournir cette
solution en deux heures de temps. En revanche c'était un travail
personnel intéressant.
Il est peut-être possible d'arriver à une programmation plus simple en
considérant la première construction comme la combinaison de deux
équilibrages de la seconde construction, mais on construira alors des
arbres déséquibrés et on devra ôter le blindage du constructeur.
Ce document a été traduit de LATEX par
HEVEA.