1. L'intérieur du polygone convexe est défini par des déterminants det(A_iA_i+1, A_iP) tous positifs.
   
   
2. Pour une arête donnée la convexité de C_n entraîne que l'arête A_iA_i+1 est visible de P, si et seulement si le déterminant det(A_iA_i+1, A_iP) est négatif. Intuitivement, un rayon lumineux partant de P et frappant l'arête pointe alors vers l'intérieur de C_n. Un sommets est éclairé lorsqu'une au moins des arêtes qui le touchent est visible. Il existe alors deux sommets importants, le premier sommet visible et le dernier en suivant le sens positif de rotation (sur la figure A₂ et A₄).
   
   Or, on peut fabriquer l'enveloppe convexe de C_n union {P} en supprimant toutes les arêtes visibles de C_n et en ajoutant une arête du premier sommet visible à P suivie d'une arête de P au dernier sommet visible. On obtient alors le polygone.
   
   
   
   
3. La méthode consiste à attendre d'avoir trois points (un triangle) et à les ordonner dans le sens positif (det(A₀A₁, A₁A₂) > 0). On peut ensuite construire l'enveloppe convexe incrémentalement, selon la question précédente. Une extension peut demander le parcours complet des points de l'enveloppe (si par exemple A₀ est le dernier point visible). Le coût est donc au pire quadratique. Il est atteint lorsque tous les points sont dans l'enveloppe convexe. et que les parcours commencent au dernier sommet visible.
   
   
4. Avec des points triés, chaque nouveau point appartient nécessairement à l'enveloppe convexe construite et au tour suivant ce point sera nécessairement éclairé. On peut alors trouver le dernier point éclairé en tournant dans le sens trigonométrique et le premier point éclairé en tournant dans l'autre sens. Une liste doublement chaînée permet cette opération. Si on trouve p côtés éclairés, on aura calculé p+2 déterminants (coût en p), et on enlèvera p-1 points (opération en coût constant). Un point donné est ajouté une fois et enlevé au plus une fois. L'algorithme est linéaire, car on peut associer un coût constant à chaque point (un déterminant si le point est enlevé, deux déterminants et une modification de la liste des sommets au moment de l'ajout).
   
   <<<<<<< index.tex
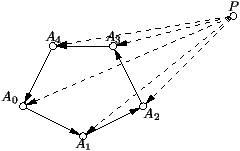
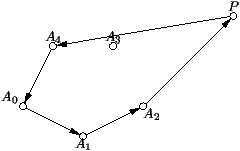
5. Voici le code d'une classe Convexe qui réalise le calcul incrémental de l'enveloppe convexe. Les sommets de l'enveloppes sont dans le champ cvx sous forme d'une liste bouclée de points. Cette structure de donnée délicate à manipulér est ici indiquée. En effet, une telle liste ressemble fortement aux dessins des enveloppes : des points reliés par des flèches.

   class Convexe {   PointList cvx ; // Liste des sommets. Attention, c'est une liste bouclée   // Travail sur l'enveloppe convexe.   // Renvoie un entier r    //    - r < 0  -> q est à droite du vecteur p1 p2   //    - r > 0  -> q est à gauche du vecteur p1 p2   //    - r == 0 -> q p1 p2 alignés   static private int det(PointList q, PointList p1, PointList p2) {     int r =       (q.y - p1.y) * (p2.x - p1.x) - (q.x - p1.x) * (p2.y - p1.y) ;     return r ;   }   // Fabrication d'un triangle comme liste bouclée de trois points   static private PointList triangle (PointList p1, PointList p2, PointList p3) {     PointList r3 = new PointList(p3.x, p3.y, null) ;     PointList r2 = new PointList(p2.x, p2.y, r3) ;     PointList r1 = new PointList(p1.x, p1.y, r2) ;     r3.next = r1 ;     return r1 ;   }   // Étendre l'enveloppe convexe (liste bouclée cvx)   // Le point ajouté est le premier de l'argument p   // etendre renvoie un booléen, qui indique un changement de l'enveloppe.  boolean etendre(PointList p) {     if (cvx == null) {       PointList p1 = p ;       if (p1.next == null)  return false ;       PointList p2 = p1.next ;       if (p2.next == null) return false ;       PointList p3 = p2.next ;       if (det(p1, p2, p3) < 0) {         cvx = triangle(p1,p2,p3) ;       } else {         cvx = triangle(p1,p3,p2) ;       }       return true ;     } else {       PointList first = null , last = null ;       PointList q ;       int prev = NONE ;       int edge ;       // Recherche des transitions entre ombre et lumière       q = cvx ;       do {         if (det(p, q, q.next) >= 0) {           edge = LIGHT ;           if (prev == SHADOW) first = q ;         } else {           edge = SHADOW ;           if (prev == LIGHT) last = q ;         }         prev = edge ;         q = q.next ;       } while (q != cvx) ;       // Examen de l'arc issu du premier point       if (det(p, q, q.next) >= 0) {         if (prev == SHADOW) first = q ;       } else {         if (prev == LIGHT) last = q ;       }       // Le point ajouté est à l'intérieur       if (last == null) return false ;       // Suppression des sommets éclairés, et ajout du nouveau point       cvx = new PointList(p.x, p.y, last) ;       first.next = cvx ;       return true ;     }   } }

   
   
   
6. L'extension de l'enveloppe convexe est en fait correctement traitée. Un côté est considéré éclairé par un point aligné. Si le point P est situé sur le côte strico-sensu, l'effet sera d'ajouter un point inutile à l'enveloppe convexe. Sinon un point devenu inutile sera enlevé.
   
   En revanche la collecte des trois premiers points doit être changée pour devenir celle des trois premiers points non-alignés.