Le resultat est immédiat pour Σ = F, car il n'y qu'une seule production.
Considérons P. Une ambiguïté éventuelle porte d'abord sur le choix d'une des trois production. Soit :
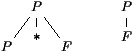
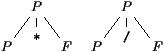
En toute complétude il faut aussi considérer le cas ou l'application d'une production peut se faire de deux manières différentes. Ici c'est impossible car F ne peut être qu'un int et donc l'avant dernier symbole de α determine non seulement une production unique, mais aussi une façon unique de l'utiliser.
Pour bien comprendre le problème, on peut caractériser l'ambiguïté dite d'associativité de la première gramaire ainsi :
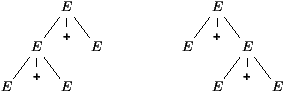
On montre ensuite que les arbres de racine E sont pareillement déterminés ce qui entraîne la non-ambiguïté.
S → E |
E → P E → E + P E → E - P |
P → F P → P * F P → P / F |
F → int F → + F F → - F
F → ( E ) |
|
private String parseF() { switch (tok.nature) { case Token.SUB: Token op = tok ; step() ; return echo ("0", op, parseF()) ; case Token.ADD: step() ; return parseF() ; case Token.OPAR: step() ; String r = parseE() ; if (tok.nature != Token.CPAR) error(")", tok) ; step() ; return r ; default: return readInt() ; } } |
Prouvons maintenant la non-ambiguïté, qui semble bien assurée car nous utilisons quotidiennement cette grammaire sans quiproquo aucun.
Soit donc un mot α dérivé d'un non-terminal Σ. Le cas Σ = F est facile, le premier symbole du flux déterminant le choix d'une production.
On considère ensuite seulement un example.
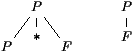
On se sert d'un lemme de bon-parenthésage. On peut montrer facilement que tout mot dérivé α d'un non-terminal comprend autant de parenthèses ouvrantes que fermantes. Mais plus précisément, tout préfixe de α contient plus (au sens large) d'ouvrantes que de fermantes, tandis que tout suffixe de α contient moins (toujours au sens large) d'ouvrantes que de fermantes.
En cas d'ambiguïté, donc, on est en raison de la nécessaire parenthèse fermante qui termine le mot α, et de la parenthèse ouvrante qui le commence presque, nécessairement dans le cas suivant.
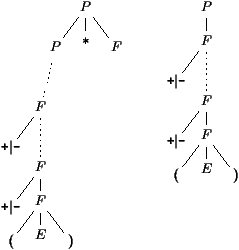
Autrement dit, α se décompose nécessairement d'une part en β ( η ) γ et d'autre part en β ( η' ) où β est une suite peut-être vide de + et de -, tandis que η et η' dérivent de E. Soit η ) est un préfixe de η'. Or η ) contient une fermante de plus que d'ouvrantes, contradiction.
O → O + int O → int |
S → int + S S → int |
E → O * E → S / |
Ici, on peut s'en tirer en lisant de droite à gauche, mais c'est s'éloigner de principe du flux. Par ailleurs, ça ne fonctionnera pas toujours. Considérer par exemple :
E → O * S E → S / O |