1. Les terminaux sont les quatre symboles des opérations plus les entiers. Les non-terminaux sont définis par les productions à savoir S et E.
  2. Bon.
    1. Il faut dériver le calcul d'Oscar à partir du symbole de départ S. Le non-termimal réduit à chaque étape est comme ça et son remplacement est comme ci.
      S
      		→
      E
      		→
      E
      		+ E
      		→ 1 +
      E
      		→ 1 +
      E
      		* E
      		→ 1 + 2 *
      E
      		→ 1 + 2 * 3


    2. Il faut montrer que l'on ne peut pas produire 1 + - 2. Il suffit de remarquer que l'on ne peut pas dériver le mot vide à partir de E, et donc que l'on ne peut pas dériver, toujours à partir de E, de mots de la forme α op ou op β, où α et β sont des mots de symboles de la grammaire.

      Une autre façon de voir est de dire que les mots du language défini par la grammaire sont de la forme int {op int}* (suite alternée d'entiers et d'opérateurs commençant et finissant par un entier). L'inclusion est immédiate. Réciproquement, soit α, un mot de la forme E {op E}*, montrons que α dérive de E (c'est à dire que E peut se réécrire en α). On raisonne par induction :
      • Le cas de base, α = E est immédiat
      • Si α = E op β, alors par hypothèse d'induction on a E ⇒*β et donc : α = E op β ⇐*E op E ← E.
      C'est terminé car tout mot de la forme int {int op}* dérive d'un mot de la forme E {E op}* (en appliquent la production E → int), qui lui même, par le lemme précédent dérive de E et donc de S.

    3. On peut exprimer les choix possibles pour Oscar à l'aide d'un arbre :
        S   →   E (16)   →   E + E (8)   →   1 + E   →   1 + E * E (2)   →   1 + 2 * E   →   1 + 2 * 3
                ↓       ↓               ↓  
                E * E (8)       E + E * E (6)               1 + E * 3   →   1 + 2 * 3  
      On distingue donc seize façons différentes de montrer que Oscar a bien produit un calcul (une expression arithmétique). Il en va de même pour Amélie et Samir.

    4. Pamela peut s'en tirer grâce au zéro :
      2 + 0 - 1
  3. Oscar a effectué les opérations de la gauche vers la droite, tandis que Samir a effectué les opérations de la droite vers la gauche. L'instituteur dira qu'il faut effectuer les multiplications (et les divisions) avant les additions (et les soustraction). Si il a le temps, il dira aussi que si deux opérations identiques se suivent, alors il faut effectivement suivre la méthode d'Oscar. Un elève malin lui fera alors remarquer que dans le cas de deux additions par exemple, l'ordre n'a pas d'importance.

  4. Deux façons de calculer 1 + 2 * 3. Comme Oscar.
    1 + 2 * 3 ←
    E
    		[1] + 2 * 3 ←
    E[1] +
    E
    		[2]
    		* 3 ←
    E
    		[3] * 3 ←
    E[3] *
    E
    		[3]
    		←
    E
    		[9]
    Comme Samir.
    1 + 2 * 3 ← 1 + 2 *
    E
    		[3] ← 1 +
    E
    		[2] * E[3]
    		← 1 +
    E
    		[6] ←
    E
    		[1] + E[6]
    		←
    E
    		[7]
    Sur cet exemple on voit assez bien qu'il n'y a au fond que deux façons de comprendre l'expression arithmétique : calculer d'abord l'addition (comme Oscar) ou d'abord la multiplication (comme Samir). Les autres choix ne sont pas significatifs, on peut par exemple inverser les deux premières étapes de l'analyse, sans que celle-ci en soit essentiellement changée.

    Les choses sont sans doute un peu plus claires, si on ne réécrit plus des mots lors des dérivations mais des arbres. C'est alors uniquement l'arbre final qui caractérise la dérivation. Ici ça nous donnera, pour la dérivation Oscar.
    Tandis que l'arbre final de la dérivation Samir est le suivant.

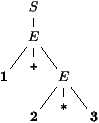
    Faisons deux remarques instructives.
    Deux grammaires.
    Oscar
    S → E         E → int
    E → E + int          E → E - int          E → E * int          E → E / int
    Samir
    S → E         E → int
    E → int + E          E → int - E          E → int * E          E → int / E
    Ces grammaires permettent bien d'effectuer tous les calculs possibles et spécifient bien un résultat unique (elle sont équivalentes à la grammaire de départ et non-ambigües). Prenons le cas d'Oscar et d'un mot int1 op int2 op … op intn. La seule façon de remonter vers S est la suivante :
    int1 op int2 op … op intn ←
    E
    		op int2
    		op … op intn ←
    E
    		op … op intn ←
    E
    		op intn
    		←
    S
  5. Voici la grammaire de l'instituteur :
    S → E
     
    E → P          E → E + P          E → E - P
     
    P → F          P → P * F          P → P / F
     
    F → int
    On peut la paraphraser en disant
    1. Une expression est une somme de produits de facteurs.
    2. Les sommes (et les produits) « penchent à gauche ».

    La non-ambiguïté de cette grammaire semble un peu pénible à prouver proprement (l'ordre des opérations est plus libre que dans le cas des deux élèves), mais il semble clair qu'elle s'apparente à celle de Samir, et qu'elle exprime les priorités traditionnelles des opérations.