Solution de l'exercice 4

Un appel à dff renvoie une forêt, telle que produite par un parcours en profondeur d'abord du graphe.
Et voilà, les arcs du graphe qui ne sont pas des arcs de l'arbre sont indiqués et identifiés.
Les arcs transverses etc. du graphe sont définis dans le poly, figure 1.10. On peut paraphraser cette définition en termes de forêt, il y a donc des arcs de la forêt, des arcs de descente (qui joignent un sommet à un de ses descendants dans la forêt, sans être un arc de l'arbre), des arcs de retour (qui joignent un sommet à un de ses ancêtres) et des arcs transverses (les autres !).
Les arcs transverses vont toujours de la droite vers la gauche sur le dessin. Cette propriété peut être considérée comme « évidente ». Détaillons un peu. De fait, par définition de l'arc transverse, n n'est pas un ancêtre de m ni m un ancêtre de n. Il y a alors deux cas.
- n et m n'ont pas d'ancêtre en commun, alors n et m appartiennent à deux arbres distincts de la forêt, l'arbre qui contient n étant nécessairement placé à droite de celui de m.
- n et m ont au moins un ancêtre commun, soit a l'ancêtre commun le plus profond, alors les sous-arbres de a constituent une forêt, et le raisonnement précédent s'applique.
Une définition de l'ordre préfixe. Pour un arbre :
PR(n,F) = n PR(F)

Et une forêt :
PR(є) = є (liste vide), PR(T,F) = PR(T) PR(F)
On remarque que les arcs de l'arbre et de descente ne sont pas discriminables à l'aide des ordres et que les arcs de retour sont les seuls dont la source précède la cible selon l'ordre postfixe.
n → m préfixe postfixe

F ≤ ≥

D ≤ ≥

R ≥ ≤

T ≥ ≥

On note aussi que la propriété des arcs transverses est bien visible.
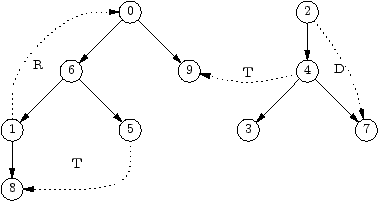
Montrons qu'il y a des arcs de retour si et seulement si le graphe contient un cycle. Le sens direct est facile, puisque par définition il existe d'une part l'arc de retour n → m et d'autre part un chemin de l'arbre de l'ancêtre m à son descendant n.
Réciproquement, soit un cycle n → m → … → n. Montrons alors que l'un des arcs du cycle est de retour. Sans perte de généralité, n est le plus petit sommet du cycle selon l'ordre postfixe et n → m est un arc de retour.
Notons que dans le poly, les arcs de retour sont identifiés à l'aide d'un coloriage BLANC → GRIS → NOIR des sommets. Un sommet étant gris lors de la construction de l'arbre dont il est la racine (et donc de l'exploration des ses descendants).