-
Si s = t (par exemple), alors s n'étant pas un point
d'articulation on
peut construire un chemin de s' à t' ne passant pas par s' et donc
un cycle.
- Sinon, le graphe étant connexe, il existe un chemin de s à t que l'on peut supposer simple. Prenons un arc de ce chemin u ↔ u' distinct des deux chemins des extrémités. Par induction il existe deux cycles contenant l'un les arcs s ↔ s' et u ↔ u', l'autre contenant les arcs t ↔ t' et u ↔ u'. En orientant les notations on peut faire que Cs et Ct sont écrits comme s ↔ … ↔ u ↔ u' ↔ … ↔ s et t ↔ … ↔ u ↔ u' ↔ … ↔ t. Soit w le premier sommet commun à Cs et Ct et w' le dernier sommet commun. Les sommets w et w' existent (car les deux cycles commencent et finissent par des sommets distincts, et contiennent des sommets communs) et sont distincts (w doit apparaître avant u ou lui être égal, w' doit apparaître après u' ou lui être égal, et u distinct de u'). On peut ensuite en « enlevant » les parties des cycles comprises entre w et w', produire un cycle s ↔ … ↔ w ↔ … ↔ t ↔ … ↔ w' ↔ … ↔ s, qui contient les arcs s ↔ s' (au début ou à la fin) et t ↔ t' (avant ou après t).
Réciproquement (si j'ose dire). Soit un graphe contenant un point d'articulation a. Il existe donc deux sommets distincts s et t, reliés par un chemin simple s ↔ s' ↔ … ↔ a ↔ … ↔ t' ↔ t. Il ne peut pas exister de cycle contenant à la fois les arcs, s ↔ s' et t ↔ t', car il n'existe pas de cycle contenant à la fois s et t. En effet il existerait alors un chemin de s à t ne passant pas par a.
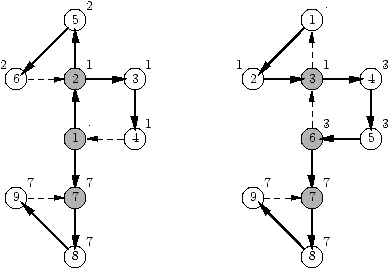
lowN >= num[s] soit vrai deux
fois. C'est le cas avec le graphe suivant pour le sommet numéroté 2.
doFind(s,_) calcule
lowpt[s], qui est le plus petit numéro de sommet dans l'ensemble
{ s } ∪ { t, s →* -→ t}.Or, soit a distinct de la racine, n un fils de a dans (X,T) (il existe a → n). Si lowpt[n] ≤ num[a] alors a est un point d'articulation, car il n'existe aucun arc du graphe d'origine entre un ancêtre strict de a et n qui ne passe pas par a. En effet, tous les chemins (du graphe d'origine) ne passant pas par a restent confinés au sous-arbre de racine n, puisque les éventuels arcs de retour issus d'un sommet de Tn pointent vers des ancêtres de leur origine qui sont nécessairement des sommets de Tn.
Si lowpt[n] > num[a] alors ont peut construire un chemin ne passant pas par a à tout autre sommet du graphe, en employant au besoin un arc de retour dans le bon sens et des arcs de l'arbre dans un sens indifférent.
Le cas de la racine est encore plus simple. Elle est un point d'articulation si et seulement si elle possède deux fils ou plus dans (X,T).
Enfin les feuilles (de l'arbre de recouvrement) ne peuvent pas être détectées comme point d'articulation. Or, elles ne sont jamais des points d'articulation du graphe d'origine, n'étant pas même des points d'articulation de l'arbre (non-orienté).
Le programme du poly s'abstient du test
num[n] < num[s] && n !=pere ce qui n'est pas gênant, car
alors la valeur de lowpt n'est pas changée.
En effet dans ces deux cas on a num[n] ≥ num[s], et on sait par
ailleurs lowpt[s] ≤ num[s].