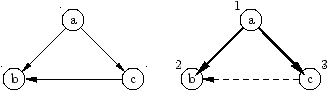1. Distinguons comme le programme deux catégories d'arcs produits. Les arcs de l'arbre de recouvrement, notés → et les arcs de retour notés -→. Il est clair que si les sommets s et t sont reliés par un de ces arcs alors, il existe un arc s ↔ t dans le graphe.

    Par ailleurs, le parcours visite tous les sommets (démontrable par un argument sur la distance au sommet de départ) et donc tous les arcs du graphe d'origine entre sommets distincts sont visités deux fois. Ces arcs sont orientés lors de la première visite. Les arcs de la forme s ↔ s sont visités une fois et ne sont pas orientés.

    Si un arc de l'arbre s → t est construit, alors un arc t -→ s ne peut pas être construit (à cause du test n !=pere).

    Si l'arc s -→ n est construit, alors l'arc n -→ s ne peut pas être construit (à cause de la condition num[n] < num[s]). L'arc s → n n'est évidemment pas construit, et l'arc n → s ne sera pas construit plus tard (car s est numéroté).

    Il y a deux nuances. D'une part il faut supposer le graphe d'origine connexe, et d'autre part les arcs s ↔ s disparaissent.

  2. Voir la figure 1. Les numéros sont indiqués.


    Figure1: Un palmier




  3. Par construction même, les arcs arbre définissent bien un arbre, au sens de la définition inductive amendée. Soit ensuite un arc de retour s -→ t. Il faut montrer l'existence d'un chemin t →* s. Soit il faut montrer que s est numéroté lors de l'appel doTarjan(t,_). Par construction, t porte un numéro plus petit que s, c'est-à-dire que t est numéroté avant s. Le sommet t ne peut donc pas être un descendant de s.

    Par ailleurs, l'arc t → s n'est pas construit. Or si, s n'était pas numéroté lors de l'appel doTarjan(t,_), alors il existerait un sommet u ancêtre strict à la fois de s et t, et deux arcs u → u1 et u → u2 distincts. tels que u1 est un ancêtre de t et u2 est un ancêtre de s. Mais alors l'arc t ↔ s serait examiné et l'arc t → s construit.

  4. Si aucun arc de retour n'est construit, alors en supprimant l'orientation des arcs de (X,T) on retrouve le graphe d'origine, qui est donc un arbre.

    Le raisonnement vaut encore pour un graphe d'origine orienté. Par conséquent si aucun arc de retour n'est construit le graphe est un arbre et est donc acyclique. À la nuance près que les cycles d'un sommet vers lui-même ne sont jamais détectés.

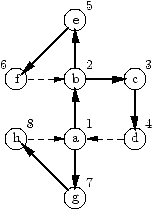
    Si un arc de retour est construit. Dans le cas non-orienté, le palmier contient un cycle, et donc, à plus forte raison le graphe d'origine.

    Ce n'est plus vrai dans le cas d'un graphe orienté. Considérer le parcours suivant.
    Notons bien que l'origine de l'arc de retour porte bien un numéro supérieur à sa cible. Un tel arc est plus exactement dénommé arc transverse (voir le poly)