1. Comme indiqué par son type, la méthode renvoie un tableau d'entiers de taille le nombre de sommet du graphe. Les éléments du tableau sont des sommets du graphe. Le tableau pere joue (entre autres) le rôle du tableau vu. Ses cases étant remplies avec des numéros de sommets au cours du parcours, il faut une valeur distincte de tous les numéros de sommets possibles pour signifier « non-vu ».

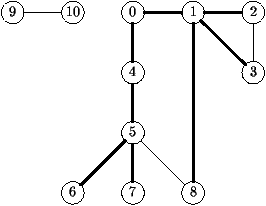
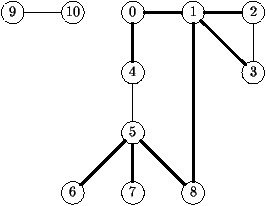
  2. Le tableau pere encode un graphe, pere[i] ==j signifiant un arc entre les sommets i et j. C'est initialement l'arbre formé de l'unique sommet s. Chaque itération de boucle interne introduit un nouveau sommet et un arc de ce nouveau sommet à un sommet de l'arbre. On ne peut ainsi créer ni boucle ni partage et tous les sommets sont reliés à la racine. (Ou mieux, tous les sommets sont reliés à la racine par un unique chemin sans répétition d'arcs.)
                    


  3. Il faut noter que l'arbre obtenu avec la pile n'est pas tout à fait celui que donnerait un parcours en profondeur d'abord. Avec notre méthode il est impossible de produire un arbre filiforme, puisque tous les arcs issus de la racine sont ajoutés en même temps.

  4. Un arbre de recouvrement est simplement un arbre dont les sommets sont la composante connexe de s et les arcs des arcs du graphe.

  5. Et voilà :
      static void findPath(int s, int ss) {
            int [] pere = findSpanningTree(ss,new Lifo ()) ;

            if (pere[s] < 0) {
          System.out.println("Pas de chemin de " + s + " à " + ss) ;
        }     else {
              int j = s ;
              while (j != ss) {
            System.out.print(j + " -> ") ;
            j = pere[j] ;
          }
          System.out.println(ss) ;
        }
      }


  6. Pour obtenir le (un) plus court chemin, il faut adopter une file. Le principe est que les sommets sont alors visités des plus proches du point de départ aux plus lointains.

    Essayons nous à le prouver, en montrant que l'arbre de recouvrement est, dans ce cas, une arborescence des plus courts chemins.

    Il suffit de montrer que si le tableau pere est bien une arborescence des plus courts chemins au début d'une itération, il en va de même à la sortie.

    Une première remarque simple (valant d'ailleurs pour tous les sacs) est que si un sommet appartient à V, alors tous ses voisins sont vus.

    Appelons distance de s à s', notée d(s') la longueur d'un plus court chemin de s à s'. Par ailleurs, définissons d comme la plus grande des distances des sommets de V (ou -1 si V est vide). Montrons que du début à la fin d'une itération, la partition des sommets en V, file (non-vide) et N s'organise selon l'un ou l'autre des schémas suivants : Ou alors, Notons que le premier schéma s'applique initialement.

    Donc on extrait s1 de la file, il y a deux selon l'organisation présente. Commençons par la seconde organisation :
    1. d(s1) = d, alors, par définition du plus court chemin les voisins de s1 sont de distance inférieure ou égale à d+1. Mais ceux des voisins qui sont ajoutés à la fin de la file sont nécessairement de distance supérieure ou égale à d+1 (car ce sont les voisins non-vus). Les arcs ajoutés à l'arborescence sont donc bien des plus court chemins. Par ailleurs s1 passe dans V ce qui ne change pas d. Si s2 existe on est donc encore dans le cadre de la seconde organisation. Sinon, il suffit de montrer que tous les sommets de distance d+1 sont dans la file. Or c'est bien le cas car les sommets de distance d sont tous dans V et donc tous leurs voisins sont vus, ceux qui sont de distance d+1 ne peuvent se trouver que dans la file,
    2. Dans la première organisation, le raisonnement est à peu près identique. Dans tous les cas d s'incrémente en d'. Si la file ne contenait qu'un élément on retrouve ensuite la première organisation (ou une file vide), sinon on retrouve la seconde organisation.
    Le raisonnement peut d'ailleurs se transformer en un programme, qui explicite les si et et ti à l'aide de deux listes cur et next.
      static void bfs(int s) {
            List cur, next=null ;
            boolean [] vu = new boolean [succ.length] ;
            int d = -1 ;

        cur =     new List(s,null) ; vu[s] = true ;
            while (cur != null) {
          d++ ; System.out.print(" [" + d + "]") ;
              for (List p = cur ; p != null ; p = p.next) {
            System.out.print(" " + p.val) ;
                for (List q = succ[p.val] ; q != null ; q = q.next) {
                  if (!vu[q.val]) {
                vu[q.val] =     true ;
                next =     new List(q.val,next) ;
              }
            }
          }
          cur = next ; next =     null ; d++ ;
        }
      }
    Notons qu'en entrant dans la boucle for (List p=..., la liste cur contient tous les sommets de distance d, tandis qu'en sortant de cette même boucle la liste next contient tous les sommets de distance d+1.

    On notera aussi que le point important est que les sommets sont introduits dans l'arborescence selon les distances croissantes. En effet la méthode bfs n'a pas tout à fait le même comportement que le parcours à l'aide d'une file, (il y a en quelque sorte inversion des listes de voisins).