Anagrammes des mots du dictionnaire, corrigé

Solution en trois parties : présentation de deux algorithmes et comparaison.

Partie I
Trouver les anagrammes, en triant

Rappelons l'algorithme. (voir l'énoncé pour plus de détails).

Fabriquer une liste de paires (mot × signature).
Trier cette liste, selon les signatures.
Maintenant, les anagrammes se suivent dans la liste triée, et on peut les afficher en un parcours de liste.

1 Liste de paires (mot × signature)

Calcul de la signature d'un mot

Les signatures sont des chaînes qui regroupent les caractères des mots dans un ordre normalisé (triés). Comme l'idée de la signature sert également au second algorithme, il semble malin de mettre son code dans une classe idoine Signature, afin d'éviter la duplication de code. Un avantage de cette technique (par rapport à un couper-coller de code) est que si on modifie le code du calcul des signatures (par ex. pour corriger un bug) il suffira de le faire une fois et non deux.

Le code lui même est très simple. L'énoncé suggérait de transformer la chaîne en tableau, de trier le tableau, et de retransformer le tableau trié en chaîne. Le code devient particulièrement simple si on emploie la méthode de tri des tableaux de caractères de la bibliothèque, la méthode statique sort(char [] t) de la classe Arrays du package java.util.

class Signature {
  static String compute(String w) {
    char [] t = w.toCharArray() ;
    java.util.Arrays.sort(t) ;
    return new String(t) ;
  }
}

Bien sûr, rien n'empêche d'écrire son propre tri. Dans ce cas, comme les mots sont toujours assez courts, un tri simple, comme par exemple le tri sélection suffit.

static void selectionSort(char [] t) {
  for (int i = 0 ; i < t.length ; i++) {
    int imin = i ; // index du minimum du tableau t[i...[
    for (int j = i+1 ; j < t.length ; j++)
      if (t[j] < t[imin]) imin = j ;
    // Échange de t[imin] et de t[i]
    char x = t[imin] ; t[imin] = t[i] ; t[i] = x ;
  }
}

À définir dans la classe Signature et à appeler à la place de java.util.Arrays.sort dans la méthode compute.

Paires

Définissons ensuite une classe des paires (mot × signature). C'est très classique.

class Pair {
  String w,sig ;

  Pair(String w) {
    this.w = w ; this.sig = Signature.compute(w) ;
  }

  // Comparaison = comparaison des signatures.
  public int compareTo(Pair p) {
    return sig.compareTo(p.sig) ;
  }
}

Remarquons juste deux points.

Le constructeur calcule la signature du mot w et la range à sa place. C'est sans grande importance, tout au plus cela nous évite un risque de confusion dans l'ordre des arguments de ce constructeur.
La comparaison de deux paires est celle de leur signature. Une méthode compareTo(Pair p) se charge de cette comparaison.

Listes de paires

Rien que de très classique encore.

class ListPair {
  Pair val ;
  ListPair next ;

  ListPair(Pair val, ListPair next) {
    this.val = val ; this.next = next ;
  }
}

2 Trier

Il va s'agir dans le cas du dictionnaire francais.txt de trier une liste de plus de 140000 éléments. Un tri efficace est nécessaire. Le tri efficace des listes est traité de façon assez complète dans le poly — section trier de grandes listes. Les conclusions du poly s'appliquent ici, il faut un tri efficace (en nlogn) et robuste (attention à la profondeur de la récursion). Un tri fusion dont la fusion est programmée itérativement fait l'affaire.

On peut très bien récupérer le code du poly (méthodes merge itérative et mergeSort) à condition de changer quelques types et surtout les comparaisons entre int (x <= y) en comparaisons entre Pair (x.compareTo(y) <= 0). Voyez les méthodes merge et sort dans la classe ListPair.

Je suis assez étonné de voir que presque personne n'a écrit un tel tri suffisamment efficace. En particulier, de nombreux codes procèdent par insertion des mots dans une liste triée, un mot (la paire plus précisément) étant inséré dès que lu. Il est clair que cette façon de procéder est moins efficace (quadratique) et ici ce n'est pas assez efficace. Enfonçons le clou : il vaut mieux d'abord construire une liste non triée (O(n)) et trier (O(n logn)), que de construire une liste triée petit à petit (O(n²)). C'est peut-être un peu contre-intuitif, mais c'est comme ça.

3 Afficher

Soit donc t, la ListPair maintenant triée de sorte que les mots de signature identique se suivent. On peut, en un parcours, repérer et afficher les mots dont les signatures sont identiques. Voici une solution.

   1  static void afficher(ListPair t) {
   2     StringBuilder ws = new StringBuilder () ;
   3     String sig = null ;
   4     int seen = 0 ;
   5     for ( ; t != null ; t = t.next) {
   6       Pair p = t.val ;
   7       if (p.sig.equals(sig)) {
   8         ws.append(" " + p.w) ; seen++ ;
   9       } else {
  10         if (seen > 1) System.out.println(ws) ;
  11         sig = p.sig ;
  12         ws = new StringBuilder() ;
  13         ws.append(p.w) ;  seen = 1 ;
  14       }
  15     }
  16     if (seen > 1) System.out.println(ws) ;;
  17   }

Et disons que afficher est une méthode d'une nouvelle classe Ana, qui sera le programme.

On utilise un StringBuilder (ws) pour accumuler les mots de signature identique et un int (seen) pour savoir facilement combien de mots contient ws. Les mots sont affichés lorsque la signature change (ligne 10) ou à la fin (ligne 16), quand il y a deux mots ou plus à afficher.

4 Tout regrouper

Voici l'enchaînement des trois étapes de l'algorithme, lire, trier, afficher (dans la classe Ana).

  static void anagrammer(WordReader in) {
    /* Lecture de tous les mots de l'entrée */
    ListPair t = null ;
    String w = null ;
    while ((w = in.read()) != null) {
      t = new ListPair(new Pair(w), t) ;
    }
    in.close() ;
    /* Tri */
    t = ListPair.sort(t) ;
    /* Affichage */
    afficher(t) ;
  }

On note que la liste est contruite à l'inverse de l'ordre de lecture. C'est sans importance, puisque la liste est ensuite triée.

Et voici la méthode main de la classe Ana.

  public static void main(String [] arg) {
    WordReader in = new WordReader (arg[0]) ;
    anagrammer(in) ;
  }

La solution est formée des sources WordReader.java, Signature.java, Pair.java, ListPair.java et Ana.java.

Partie II
Trouver les anagrammes, en hachant

Rappelons l'algorithme. On se donne une table de hachage dont les clés sont les signatures (donc des String) et les valeurs des listes de mots (donc des listes de String). Tous les mots d'une liste donnée ont la même signature et la table associe la liste à cette signature commune.

L'algorithme procède en deux temps.

Pour chaque mot du dictionnaire, calculer sa signature et ranger le mot dans la bonne liste.
Parcourir toutes les listes de la table et afficher les listes de taille supérieure ou égale à deux.

1 Construction de la table

Afin de minimiser le code écrit, nous allons employer les tables de hachage de la librairie — la classe HashMap<K,V> du package java.util, voir la section tables de hachage de la librairie du poly.

Il est également possible d'adapter le code des tables de hachage du poly (classe H). Cela pouvait simplifier l'affichage des anagrammes.

Classe des valeurs

Un bête classe ListString.

class ListString {
  String val ;
  ListString next ;

  ListString (String p, ListString next) {
    this.val = p ; this.next = next ;
  }

  // Afficher la liste p sur une ligne.
  static void afficher(ListString p) {
    if (p == null) {
      System.out.println() ;
      return ;
    }
    for ( ; p.next != null ; p = p.next) {
      System.out.print(p.val) ; System.out.print(" ") ;
    }
    System.out.println(p.val) ;
  }
}

Code ultra-classique, à part peut-être la méthode afficher qui fait bien attention à n'afficher un espace que entre deux mots, et à revenir à la ligne dans tous les cas.

Construction proprement dite

Le programme sera une nouvelle classe AnaH, dont le source commence par importer toutes les classes du package java.util.

import java.util.* ; // Pour HashMap<K,V> du package java.util
class AnaH {
…
}

Voici enfin le code de construction de la table, effectué par la méthode read.

  static HashMap<String,ListString> read(WordReader in) {
    HashMap<String,ListString> t = new HashMap<String,ListString> () ;
    String w = in.read() ;
    while (w != null) {
      String sig = Signature.compute(w) ;
      ListString p = t.get(sig) ;
      t.put(sig, new ListString(w, p)) ;
      w = in.read() ;
    }
    return t ;
  }

On note.

La réutilisation de la classe Signature (section 1 ci-dessus).
Si la clé sig n'est associée à aucune valeur dans la table t, alors t.get(sig) renvoie null (cf. la doc de la méthode get). Cela nous arrange ici, car null représente bien une liste vide de mots.

2 Affichage des anagrammes

La méthode ListString.afficher(ListString p) déjà écrite convient pour afficher une ligne d'anagrammes. Il faut itérer sur toutes les valeurs de la table et appeler afficher pour celles de ces valeurs qui sont de longueur deux ou plus. Comment faire ?

Un problème similaire (afficher les associations d'une HashMap) a déjà été traité lors de l'amphi 04.

Ici,

Un objet HashMap<K,V> possède une méthode values() qui renvoie un objet Collection<V> (comme un ensemble mais avec des doublons possibles).
Les objets Collection<E> implémentent l'interface Iterable<E>, ce qui permet d'itérer sur tous leurs éléments ainsi.
   Collection<E> col = … ;
   for (E e : col) {
     // Traiter l'élément e.
   }
Ce que la doc appelle le “foreach statement”. L'amphi 04 donne plus de détails.

Bref, on ajoute la méthode suivante à la classe AnaH.

  static void afficher(HashMap<String,ListString> t) {
    for (ListString p : t.values()) {
      if (p.next != null) {
        ListString.afficher(p) ;
      }
    }
  }

Il y a une (petite) astuce, p ci-dessus ne peut pas valoir null, puisque nous ne rangeons jamais null dans la table.

3 Tout regrouper

Voici la méthode main de la classe AnaH.

  public static void main(String [] arg) {
    /* Lecture de tous les mots de l'entrée */
    WordReader in = new WordReader (arg[0]) ;
    HashMap<String,ListString> t = read(in) ;
    in.close() ;  // J'ai ouvert, je ferme.
    /* Affichage */
    afficher(t) ;
  }

La solution complète est formée des sources WordReader.java, Signature.java, ListString.java et AnaH.java.

Partie III
Comparer, conclure

Comme suggéré dans l'énoncé, on procède aux tests suivants

% java Ana ./petit.txt | wc
% java Ana ./moyen.txt | wc
% java Ana ./francais.txt | wc

Où la commande Unix wc affiche un compte de lignes, mots et caractères de son entrée.

On procède de même avec AnaH et on obtient les mêmes résultats.

      3       9      71
    448    1000    9090
   8378   18515  168057

Il est rassurant de retrouver des comptes d'anagrammes identiques avec deux programmes différents, il est encore plus rassurant de retrouver les comptes de l'énoncé.

Pour être tout à fait rassuré, on pourrait vérifier que les anagrammes sont bien les mêmes, en triant puis comparant (commande Unix diff), en vérifiant que les mots sont bien présents dans le dictionnaire, que ce sont bien des anagrammes etc. Mais bon, on s'en tiendra à la vérification simple des comptes des anagrammes.

Reste à analyser la performance. Nous mesurons le temps d'exécution avec la comande Unix time (sur une machine Linux, 1400Mhz).

% time -p java Ana francais.txt >/tmp/r   
real 2.78
user 1.21
sys 0.05

Les temps affichés sont en secondes, ils se décomposent en temps de l'horloge sur le mur (le vrai temps si j'ose dire), temps passé dans le code en mode utilisateur, et temps passé en mode système. Le fait que real n'est pas à peu près la somme de user et de sys s'explique difficilement sur une machine non-chargée, ce qui est le cas ici. L'anomalie semble ne se produire que pour Ana et pas pour AnaH, ce qui dénonce peut-être une fantaisie dans l'interaction entre le système de mesure du temps machine et java en cas d'allocation abondante.

On remarque par ailleurs que les temps real sont à peu près stables d'un essai à l'autre. Nous choisissons de noter les temps real.

	`petit.txt`	`moyen.txt`	`francais.txt`
`Ana`	0.09	0.13	2.7
`AnaH`	0.09	0.15	1.4

De ces chiffres on peut conclure que les deux programmes sont rapides. À vrai dire les deux programmes répondent parfaitement au problème posé, dans la limite des dictionnaires donnés (dont une caractéristique pertinente est le nombre faible d'anagrammes en regard du nombre de mots des dictionnaires).

Certes, Ana semble un peu plus lent que AnaH dans l'expérience francais.txt. Mais on ne peut pas franchement conclure, en raison du petit nombre de mesures et des temps relativement faibles. Pour en avoir le cœur net, on peut se livrer a des expériences supplémentaires. On concatène d'abord quatre dictionnaires (français deux fois, britannique et américain), puis on sélectione diverses lignes de ce gros fichier (avec un programme par nous écrit), afin d'obtenir des listes de mots de taille variable. 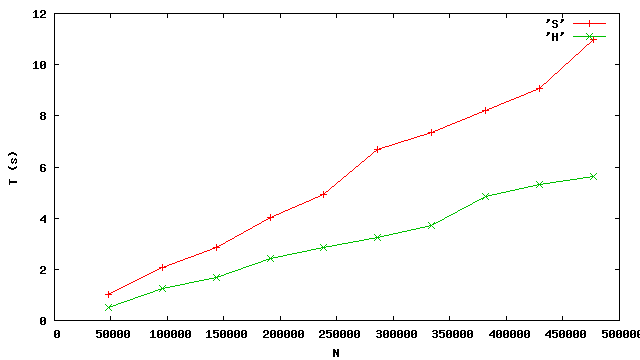En suite, on mesure le temps d'exécution (real) de Ana et AnaH (respectivement S et H, ci-dessous). Enfin on trace un graphique en fonction du nombre de mots des entrées.

On voit alors que les deux programmes semblent se comporter à peu près linéairement, AnaH étant sensiblement plus rapide. Toutefois, en programmant encore mieux le tri, (c'est possible, voir le poly) on devrait pouvoir améliorer Ana.

On peut aussi comparer la taille du code des deux programmes, en comptant les lignes.

% wc -l Signature.java Pair.java ListPair.java Ana.java
   7 Signature.java
  12 Pair.java
  62 ListPair.java
  38 Ana.java
 119 total
% wc -l Signature.java ListString.java AnaH.java
   7 Signature.java
  20 ListString.java
  33 AnaH.java
  60 total

C'est très grossier, en particulier les commentaires peuvent troubler les comptes de lignes. Mais enfin, je suppose que mon style de codage est plus ou moins le même dans les deux programmes. De plus il apparaît une différence assez nette : le programme AnaH est à peu près deux fois plus court que Ana. Cela est essentiellement dû à l'emploi des tables de hachage de la librairie.

Il est aussi assez clair que AnaH est plus simple algorithmiquement parlant. Une fois compris ce qu'est une table de hachage, il n'y a plus grand chose à concevoir. Comme souvent, l'emploi des tables de hachage permet d'éviter de se poser trop de questions algorithmiques (quel est un tri efficace ?) et de les remplacer par des questions techniques (comment parcourir les valeurs de la table ?). La table de hachage, c'est la solution de l'ingénieur.

En conclusion, efficacité meilleure pour un effort de programmation moindre, on peut conclure en faveur du second algorithme.

Bonus

Voici les résultats de l'expérience déjà décrite appliquée aux programmes des élèves qui sont suffisamment efficaces pour que cela aie un sens : les courbes de A à E et H sont les tables de hachage, les lettres doublées et S sont les tris.

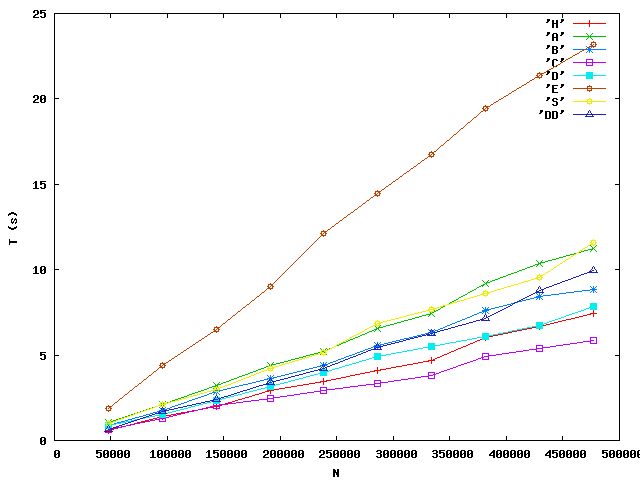
Deux points.

Tous les programmes à base de table de hachage se valent à peu près. Voici une description rapide.
- H est le corrigé.
- A et B sont très similaires (à un point suspect). L'affichage de la table se fait en relisant le dictionnaire et recalculant les signatures, c'est-à-dire en recalculant les clés. Dès lors, en cas d'anagrammes la même clé est recalculée plusieurs fois lors de cette second phase. Une seconde table de hachage des clés déjà affichées permet d'éviter les affichages répétées des anagrammes.
  La principale différence entre les deux programme réside dans le calcul des signatures. A emploie un tri fusion de tableau, B un tri selection.
- C est semblable au corrigé. L'affichage se fait par un parcours des entrées de la table, (méthode entrySet()). La légère différence de performance avec le corrigé s'explique mal.
- D et E sont des adaptations de la classe H du poly. Cela facilite l'affichage :
  // t est le tableau des listes de colision (AList)
  for (int k = 0 ; k < t.length ; k++) {
    for (AList p = t[k] ; p != null ; p = p.next) {
      ListString q = p.val ;
      if (q.next != null) ListString.afficher(q) ;
    }
  }
  La différence de performance entre les deux programmes, ici plutôt significative, s'explique par la méthode de calcul de la signature. E est ralenti par une technique plutôt bizarre de comparaison des caractères : soient c₁ et c₂ deux char, pour comparer c₁ et c₂, le programme E procède par (c₁ + "").compareTo(c₂ + "") < 0, là où c₁ < c₂ convient.
Il est notable que DD emploie un tri fusion en place, à priori plus efficace que le tri fusion non-destructif de S. Le gain existe, mais n'est pas énorme.

Enfin voici un autre test du même style effectué sur une autre machine (Linux, 64 bits, 3GHz, multiprocesseur). Les performances sont semblables, mais pas identiques, ce qui nous incite à être prudent dans nos conclusions.

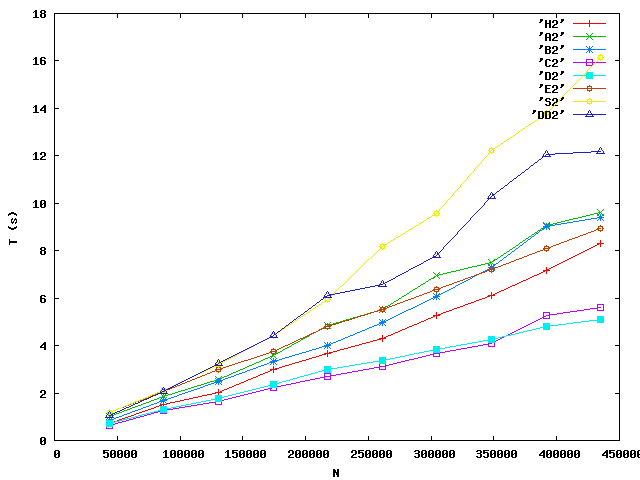
Au passage, La nouvelle machine est réputée franchement plus rapide que l'ancienne. Au vu des résultats,ce n'est pas le cas. Cela est presque certainement relié à l'implémentation de la machine virtuelle java sur une machine 64bits multiprocesseur. Il semble en particulier que la nouvelle machine pénalise les allocations mémoire abondantes et les écritures dans System.out.

Ce document a été traduit de L^AT_EX par H^EV^EA