L e caractère fini d'un programme est une notion qui se
retrouve tant dans les propriétés de terminaison, que dans celles de
puissance d'expressivité. Un programme est la description finie d'un
calcul. Cette simple remarque est à la base de la théorie de la
calculabilité. Supposons qu'on puisse avoir droit à un nombre infini
d'instructions. On n'aurait pas attendu des siècles pour connaitre la
réponse à la conjecture de Fermat. Il aurait suffit d'exécuter en
parallèle toutes les équations xn+yn = zn pour tous les
quadruplets d'entiers positifs (x,y,z,n) (n > 2) en écrivant une
astérisque sur l'imprimante si l'équation est vérifiée. Au bout d'un
temps constant, si on ne voit rien écrit sur l'imprimante, la
conjecture de Fermat est vraie. Pourtant, cette machine infinie semble
irréaliste. Non seulement la taille du programme doit être finie, mais
chaque donnée manipulée semble aussi devoir être bornée. Dans la
vérification du théorème de Fermat, les nombres deviennent
arbitrairement grands, et il semble illogique de donner un coût
constant pour calculer la somme, l'exponentielle ou l'égalité de deux
nombres arbitrairement grands. Enfin, la taille de la mémoire utilisée
pour faire un calcul importe aussi. Peut-elle être infinie? Finie
non-bornée? Doit-elle être bornée? Ce sont ces questions que nous
abordons dans ce chapitre, en considérant deux modèles de machines:
les automates finis et les machines de Turing. Il ne s'agira que d'une
première approche vers la théorie de la calculabilité, inventée par
Gödel, Church, Turing et Kleene. Cette théorie a de multiples
rapports avec la théorie des langages formels associée à l'analyse
syntaxique, ou avec la logique mathématique utilisée dans les
propriétés de correction des programmes.
| 7.1 |
Exemples de machines finies |
|
Nous commençons par passer en revue quelques exemples de machines à
nombre d'états fini.
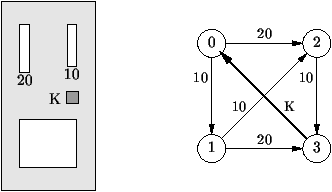
Exemple 1 Distributeur de café.
La machine de la figure 7.1 comporte deux fentes
pour les pièces de 10 et 20 centimes, et un bouton K pour obtenir un
café. Au début, le bouton K est bloqué, les deux fentes sont
ouvertes. Le café coute 30 centimes. Si on a mis suffisamment de
pièces, les fentes se ferment, le bouton K est libéré, on ne peut
plus mettre de pièces, et on peut enfoncer le bouton K. Alors un
gobelet tombe dans l'espace vide au bas de la machine, et le café se
verse dans le gobelet. L'automatisme correspondant comporte 4 états.
Dans les états 0, 1, 2, les fentes sont ouvertes, le bouton K est
bloqué. Dans l'état 4, les fentes sont fermées, le bouton K est
débloqué. Les états 0, 1, 2, 3 enregistrent le crédit courant en
multiples de 10 centimes. On passe d'un état à un autre soit en
insérant une pièce dans une des deux fentes, soit en appuyant sur le
bouton K. Au début, le distributeur est dans l'état 0. Ceci est
résumé par le schéma à droite sur la figure
7.1.
Figure 7.1 : L'automate d'un distributeur de café
Exemple 2 Distributeur de café avec un tampon de longueur 2.
L'appareil précédent ne rend pas la monnaie. Il n'autorise pas de
mettre plus de 30 centimes avant que le café ne soit versé. Nous
l'améliorons légèrement. On peut maintenant obtenir jusqu'à deux cafés
consécutivement à condition d'avoir mis 60 centimes. Pour aller plus
vite, la machine libère le bouton K dès que suffisamment de pièces
ont été introduites. Ainsi on peut mettre deux pièces de 20 centimes,
appuyer sur K, puis remettre deux autres pièces de 20 centimes, et une
de 10 centimes, puis appuyer deux fois de suite sur K, etc. Au
total, notre automatisme a maintenant les 7 états décrits sur la
figure 7.2.
Figure 7.2 : L'automate d'un distributeur de café avec mémoire
Les mécanismes de nos deux machines à café sont simples, ils décrivent
le fonctionnement d'un compteur sur un intervalle fini. L'intérêt de
cette description est qu'on peut se contenter de l'automate pour
chacune de ces machines. Ce n'est pas la peine de disposer d'un
compteur. De simples dispositifs matériels peuvent réaliser notre
automate. Il y a peu d'états, peu de transitions, le tout est bien sûr
fini. On dit que l'automate décrivant notre machine est un automate
fini. Beaucoup d'automatismes de la vie courante (feux rouges,
barrières, etc) sont des automates finis.
Les circuits logiques sont un autre exemple de machines finies. Les
circuits ont une partie combinatoire (enchaînements de portes pour
calculer une fonction booléenne) et une partie de contrôle fini pour
assurer la séquence entre les parties combinatoires. Par exemple, un
processeur commence le traitement d'une instruction machine après
avoir fini celui de celle qui la précède.
Exemple 3 Additionneur binaire série.
A partir d'un additionneur sur 1-bit ADD1, on fabrique un
additionneur série sur n bits. La porte ADD1 a un fil d'entrée
pour les entreés x et y sérialisées, et un autre fil d'entrée pour
la retenue entrante cin et deux fils de sortie pour la somme
résultat s et la retenue sortante cout. Pour faire un
additionneur sur n bits, la retenue de sortie reboucle sur l'entrée
(après amplification), et on suppose le dispositif synchronisé sur une
horloge pour faire d'abord entrer cin et x, puis y, puis
laisser sortir s et cout, comme indiqué sur la
figure 7.3.
Les données x et y arrivent entrelacées sur un seul fil
d'entrée. L'additionneur réagit à des données de la forme x0 y0 x1
y1... xn yn où xi et yi sont les (i+1)-ème bit en
partant de la droite dans la représentation binaire de x et de
y. Le résultat produit est s0 s1 ... sn représentant en
binaire la somme s de x et de y, en sortant d'abord le bit de
poids faible s0, puis le suivant s1, etc. Sur la
figure 7.4, le fonctionnement de
l'additionneur sur n bits est décrit par un petit automate. Au
début, on est dans l'état 0. Si on a x0 = 0, on évolue vers
l'état 0x, sinon on va en 1x. Dans l'état 0x, si on a
y0=0, on va en 0y et alors on envoie 0 comme résultat pour
s0, et on revient dans l'état 0 pour lire x1, puis y1. On
recommence le même raisonnement avec x1 et y1. Etc. Si dans
l'état 0x, on a y0=1, on va en 1y et on envoie 1 comme
résultat pour s0, et on revient dans l'état 0 pour aussi traiter
x1, et y1. Etc.
Les états 0 et 1 sont des états où on lit un xi avec la retenue
courante valant respectivement 0 ou 1. Les états vx et vy
signifient que la valeur v a été accumulée en additionnant la
retenue courante à la valeur respectivement de xi, ou de xi et
yi. La transtion !v signifie que v est la valeur de si.
La description du fonctionnement de cette machine est proche de celui
fait pour la machine à café. Il consiste encore à faire un calcul sur
un domaine à peu de valeurs. Il est aussi très simple car le
séquencement de l'additionneur est trivial. Dans le cas de circuits
plus réalistes (par exemple un processeur avec plusieurs niveaux de
pipeline), le nombre d'états peut être beaucoup plus grand.
Figure 7.3 : Additionneur série
Figure 7.4 : L'automate d'un additionneur série
Exemple 4 Analyseur lexical.
Dans la section 2.5, le code d'un analyseur
lexical a été présenté. Il consistait à trouver dans un chaîne de
caractères des lexèmes comme ceux correspondants aux identificateurs,
aux nombres, ou opérateurs utilisés dans les expressions
arithmétiques. Le code de notre analyseur correspond exactement à
l'automate fini de la
figure 7.5. Dans l'état initial, on
saute tous les caractères blancs (espace, tabulation, retour
ligne). Si on rencontre une lettre, c'est le début d'un
identificateur, c'est-à-dire une suite de lettres et de chiffres. On
génère le lexème dès que le caractère courant n'est plus ni une
lettre, ni un chiffre. Dans l'état 2, on génère le lexème
correspondant à un nombre. Dans l'état 3, il s'agit d'un opérateur.
Figure 7.5 : L'automate d'un analyseur lexical
Exemple 5 Mots avec des nombres pairs de a et de b.
Dans cet exemple, plus académique, il s'agit de reconnaitre les mots
sur l'alphabet {a, b} contenant un nombre pair de a et de
b. On considère l'automate de la figure 7.6. On
démarre dans l'état 0 et on accepte un mot quand on revient à
l'état 0 après avoir lu toutes ses lettres. Si on lit un a, on
passe à l'état 1, si c'est un b on passe à l'état 2. L'état 1
signifie qu'on a lu un nombre impair de a et un nombre pair de b;
l'état 2 veut dire qu'on a lu un nombre pair de a et un nombre
impair de b. Si dans l'état 1, on lit un a on revient à l'état
0; si dans l'état 1, on lit un b, on passe à un état 3 (nombre
impair de a et nombre impair de b); etc. Remarquer que la chaîne
vide est acceptée puisque contenant un nombre nul de a et de b.
Figure 7.6 : Mots contenant un nombre pair de a et de b
Les exemples précédents sont des exemples d'automates finis. Cette
structure a été définie dans les années 50; elle constitue le premier
exemple de machine abstraite considérée dans ce chapitre. Un automate
fini A est un quintuplet (Q, S, d, q0, F) où
-
S est l'alphabet d'entrée sur lequel sont construits les mots
à reconnaitre,
- Q est un ensemble fini d'états,
- q0 Î Q est l'état initial,
- F Ì Q est l'ensemble des états de fin,
- d est une fonction Q × S ® Q, dite fonction de
transition.
L'automate est à tout moment dans un des états de Q; au début il est
dans l'état q0. L'automate est une machine finie permettant de
reconnaître des mots sur l'alphabet S. Pour un mot w de
S*, au début, l'automate lit la première lettre a0 de
w. Il passe donc dans l'état q1 = d(q0, a0). Puis il lit
la deuxième lettre a1 de w et il passe dans l'état q2 =
d(q1, a1), etc., jusqu'à qn-1 après avoir lu les n
lettres du mot w. Si qn-1 Î F, le mot w est accepté par
l'automate. Sinon, le mot w est refusé.
Dans l'exemple des mots avec un nombre pair de a et
de b. On a S = {a, b}, Q = {0, 1, 2, 3 }, q0 = 0, F = {
0 }, et d donné par les formules suivantes:
| d(0, a) = 1 |
|
d(1, a) = 0 |
|
d(2, a) = 3 |
|
d(3, a) = 2 |
| d(0, b) = 2 |
|
d(1, b) = 3 |
|
d(2, b) = 0 |
|
d(3, b) = 1 |
Formellement, la fonction de transition d de type Q ×
S* ® Q devient la fonction d de type Q ×
S* ® Q, définie récursivement sur w comme suit:
d(q, e) = q
d(q, aw) = d(d(q,a),w)
Le langage T(A) reconnu par l'automate
A est défini par:
T(A) = { w | d(q0, w) Î F }
Cette définition ne fait que formaliser la discussion précédente. A
partir de q0, on doit finir dans un état de fin dans
F. Traditionnellement les automates sont représentés par un graphe
dont les sommets sont les états, les arcs sont étiquetés par la lettre
permettant la transition. Les états de fin sont marqués par des
sommets dont partent des flèches tiretées vers l'extérieur. L'état
initial est également marqué par une flèche tiretée incidente.
Figure 7.7 : Un automate fini
Graphiquement, comme indiqué sur la figure 7.7,
l'automate est une machine disposant d'une bande de lecture, d'une
tête de lecture, d'un état courant q, et d'une fonction de
transition d. Au début la tête de lecture est sous le premier
caractère de la bande à gauche. A chaque transition, en fonction de
son état interne et du caractère sous la tête de lecture, il évolue
vers un nouvel état en se déplacant d'un caractère vers la droite.
L'automte se déplace vers la droite en lisant tous les caractères de
la bande, et on regarde l'état final pour voir s'il est dans F.
Remarquons que la bande de lecture est non-modifiable.
La représentation d'un automate fini peut se faire en dur dans un
programme. Plusieurs manières existent: avoir une variable explicite
pour l'état (comme dans la fonction accepter suivante), faire
coïncider le contrôle du programme avec l'état (certains points
du programme correspondent aux valeurs de l'état, et on se branche à
ces points du programme en fonction de l'état désiré), ou tabuler la
fonction de transition comme dans la fonction accepter1
suivante.
static boolean accepter (String w) {
int n = w.length();
int q = 0;
for (int i = 0; i < n; ++i) {
char c = w.charAt(i);
switch (q) {
case 0: if (c == 'a') q = 1;
else if (c == 'b') q = 2;
else return false;
break;
case 1: if (c == 'a') q = 0;
else if (c == 'b') q = 3;
else return false;
break;
case 2: if (c == 'a') q = 3;
else if (c == 'b') q = 0;
break;
case 3: if (c == 'a') q = 2;
else if (c == 'b') q = 1;
else return false;
break;
}
}
return q == 0;
}
static boolean accepter1 (String w, int[ ][ ] delta) {
int n = w.length();
int q = 0;
for (int i = 0; i < n; ++i) {
char c = w.charAt(i);
q = delta [q][c];
}
return q == 0;
} |
Toutefois, la solution qui consiste à tabuler la fonction de
transition pose souvent un problème de place mémoire. En Java, un
caractère est représenté sur 16 bits, le tableau peut donc avoir
65536 n éléments pour un automate de n états. Comme ce tableau est
souvent creux, on a intérêt à le compresser. Dans notre exemple, c'est
simple puisque seuls les caractères a et b importent, mais en
général cela peut être plus ardu. Une solution potentielle consiste à
faire des listes d'association pour chaque état, en adoptant une
représentation proche de celle des graphes avec des tableaux de
successeurs adoptée au chapitre 1.
| 7.3 |
Automates finis non-déterministes |
|
La définition précédente des automates finis leur donne un
comportement déterministe. A tout moment, une seule transition est
possible en fonction de l'état q et de la lettre sous la tête de
lecture a. Dans les automates non-déterministes, plusieurs
transitions sont possibles.
Exemple 6 Mots avec deux a consécutifs.
Il s'agit de reconnaitre les mots sur l'alphabet {a, b} contenant
un facteur aa. On les reconnait par l'automate de la
figure 7.8(i). Dans l'état initial 0, si le mot w à
reconnaitre commence par b, on reste dans l'état 0; si la première
lettre de w est un a, on a le choix d'aller en 0 ou en 1. Dans
l'état 1, on passe à l'état 2 avec un a; avec un b, l'automate
se bloque, aucune transition n'est possible. Etc. L'état 2 est le
seul état de fin. Les mots acceptés sont tous ceux pour lesquels il
existe une série de choix pouvant mener à l'état 2. Ce sont bien
tous les mots contenant un facteur aa.
Figure 7.8 : Mots contenant deux a consécutifs: (i) à gauche l'automate
non-détermiste, (ii) à droite, l'automate déterministe.
L'intérêt de la présentation non-déterministe des automates finis est
que sa description est souvent plus succincte et naturelle qu'une
version déterministe équivalente. Par exemple, les mots reconnus par
l'automate non-déterministe de la figure 6(i)
sont aussi reconnus par l'automate déterministe de la
figure 6(ii). La présentation déterministe est
légèrement plus compliquée, mais cela peut être plus compliquée encore
comme dans l'exemple suivant.
Exemple 7 Mots avec a en avant-dernière lettre.
Il s'agit de reconnaitre les mots sur l'alphabet {a, b} décrits
par l'expression régulière (a +b)*a(a+b). On les reconnait par les
automates de la figure 7.9. On remarque que
l'automate non-déterministe correspond exactement à l'expression
régulière, alors que l'automate déterministe implémente un système de
registre à retard pour accepter le mot dans les états 2 ou 3.
Figure 7.9 : Mots contenant a en avant-dernière position: (i) à
gauche l'automate non-détermiste, (ii) à droite, l'automate
déterministe.
En fait, le nombre d'états devient encore plus grand si on cherche à
reconnaitre les mots dont la n-ième lettre à partir de la fin est a.
Exercice 48 Trouver le nombre d'états pour l'automate déterministe
reconnaissant les mots dont la 3-ième lettre à partir de la fin est
a.
La définition formelle d'un automate fini non-déterministe
A est pratiquement identique à celle des automates
déterministes; seule la fonction de transition diffère. Donc un
automate fini non-déterministe est un quintuplet (Q, S, d, q0,
F) où
-
S est l'alphabet d'entrée sur lequel sont construits les mots
à reconnaitre,
- Q est un ensemble fini d'états,
- q0 Î Q est l'état initial,
- F Ì Q est l'ensemble des états de fin,
- d est une fonction Q × S ® 2Q est la fonction de
transition.
Dans l'automate de l'exemple de la figure 7.8, on a S =
{a, b}, Q = {0, 1, 2 }, q0 = 0, F = { 2 }, et d
donné par les équations suivantes:
| d(0, a) = {0, 1 } |
|
d(1, a) = {2 } |
|
d(2, a) = {2 } |
| d(0, b) = {0 } |
|
d(1, b) = Ø |
|
d(2, b) = {2 } |
d(q, e) = { q }
d(q, wa) = {q'' | q'Î d(q,w), q'' Î d(q',a) }
Le langage T(A) reconnu par l'automate
A est défini par:
T(A) = { w | d(q0, w) Ç F ¹ Ø }
Pour écrire une fonction ndAccepter implémentant la fonction
d'acceptation d'un automate fini non-déterministe, on peut écrire le
programme non-déterministe suivant:
class NDAutomate {
int q0;
Liste[ ][ ] delta;
Liste fin;
NDAutomate (int q, Liste f, Liste[ ][ ]d) { q0 = q; delta = d; fin = f; }
static boolean ndAccepter (String w, NDAutomate a) {
int n = w.length();
int q = a.q0;
for (int i = 0; i < n; ++i) {
int c = w.charAt(i);
Liste e = a.delta [q][c];
if (e == null) return false;
int k = Math.max(1,
(int)(Math.ceil(Math.random() * Liste.longueur(e))));
q = Liste.kieme(e, k);
}
return Liste.estDans(a.fin, q);
}
} |
qui utilise une fonction de tirage au sort pour choisir parmi les
états possibles à chaque transition. On a également besoin des fonctions
suivantes sur les ensembles d'états, réalisés ici par des listes:
class Liste {
int val;
Liste suivant;
Liste (int v, Liste x) { val = v; suivant = x; }
static int longueur (Liste x) {
if (x == null) return 0; else return 1+longueur(x.suivant);
}
static int kieme (Liste x, int k) {
if (k == 1) return x.val; else return kieme(x.suivant, k-1);
}
static boolean estDans (Liste x, int v) {
if (x == null) return false;
else return x.val == v || estDans(x.suivant, v);
}
} |
Si le résultat de ndAccepter est vrai, le mot donné en
argument est bien accepté par l'automate. En revanche, si le résultat
est faux, il n'est pas sûr qu'une exécution suivante ne puisse
retourner vrai avec la même chaîne d'entrée. Mais, on peut aussi
écrire la fonction suivante qui énumère tous les choix possibles et
qui par énumération exhaustive donne une réponse exacte sur
l'acceptation d'une chaîne de caractères par un automate fini
non-déterministe.
static boolean ndAccepter (String w, Automate a) {
return ndAccepterE (w, 0, a, a.q0);
}
static boolean ndAccepterE (String w, int i, Automate a, int q) {
int n = w.length();
if (i == n)
return Liste.estDans(a.fin, q);
else {
boolean res = false;
int c = w.charAt(i);
for (Liste e = a.delta [q][c]; e != null; e = e.suivant) {
int q1 = e.val;
res = res || ndAccepterE (w, i+1, a, q1);
}
return res;
}
} |
Conformément aux méthodes exposées dans le chapitre 4,
les appels récursifs de la fonction ndAccepterE consistent à
faire des retours en arrière (backtracking) sur la chaîne
d'entrée et revenir sur un choix différent.
Il existe bien d'autres formulations pour les automates finis en
dehors des deux principales que nous venons de voir. En voici quelques
unes qui s'obtiennent par variations sur la définition de la fonction
d de transition:
- d : Q × S È {e} ® 2Q
L'automate
non-déterministe avec transitions vides peut à tout moment, dans
l'état q avec la lettre a sous la tête de lecture, choisir entre
faire une des transitions données par d(q,a), ou d'abord faire
une transition vide qui change spontanément l'état en un état de
d(q, e). Formellement
| d(q, e) = { q } È d(q, e) |
| d(q, uav) = {q3 | q1Î d(q,u),
q2 Î d(q',a), q3 Î d(q2,v) } |
- d : Q × S* ® 2Q défini sur un sous-ensemble
fini de S*
L'automate fini non-déterministe avec transitions composées peut à
tout moment choisir une des transitions données par d(q,u)
si la lettre sous la tête de lecture est la première du mot u dans
le mot à analyser. Bien remarquer qu'on exige que le nombre de
transitions décrites par d est fini. Formellement
| d(q, e) = { q } È d(q, e)
si d(q, e) est défini |
| d(q, e) = { q } sinon |
| d(q, vuw) = {q3 | q1Î d(q,v),
q2 Î d(q1,u), q3 Î d(q2,w) } |
- d : Q × S ® 2Q × {gauche,
droite }
L'automate fini non déterministe avec
déplacement dans les 2 sens fonctionne comme un automate fini
non-déterministe, sauf qu'après avoir lu une lettre, il peut se
déplacer d'une case vers la droite, ou d'une case vers la gauche pour
relire un caractère qu'il a déja lu. Si le déplacement vers la gauche
n'est pas possible, l'automate se bloque. La condition d'arrêt est
toujours que l'état obtenu soit dans F, mais il se peut qu'on n'ait
pas lu tout le mot à reconnaitre. Formellement, nous considérons les
configurations (u,q,v) où u est le mot (strictement) à gauche de
la tête de lecture, v le mot à droite, et q l'état courant, ainsi
que la relation binaire associée ¾® sur les configurations
définie par
| (q', droite) Î d (q, a) |
Þ |
(u, q, av) ¾® (ua, q', v) |
| (q', gauche) Î d (q, a) |
Þ |
(ub, q, av) ¾® (u, q', bav) |
| T(A) = { w | (e, q0, w)
|
|
(u, q, v), qÎ F }
|
On peut donc se poser le problème de l'expressivité de ces diverses
définitions. En fait, on peut montrer qu'elles sont toutes
équivalentes. Un ensemble de mots reconnu par l'une est aussi
reconnaissable par l'autre. Nous laissons ces démonstrations en
exercice. On pourra donc choisir entre ces définitions d'automates
finis non-déterministes en fonction de la commodité d'utilisation.
| 7.4 |
Les trois théorèmes fondamentaux |
|
La théorie des automates finis est riche. Nous ne ferons que l'aborder
à travers les trois théorèmes suivants.
Théorème 1 [Rabin, Scott] Les langages reconnus par les automates
finis déterministes sont exactement ceux reconnus par les automates
finis non-déterministes.
Démonstration Trivialement les mots reconnus par un automate
déterministe le sont aussi par un automate non-déterministe, puique
les automates finis déterministes forment un cas particulier des
automates non-déterministes. Réciproquement, si A est un
automate fini non-déterministe (Q, S, d, q0, F),
considérons l'automate
A' = (2Q, S, d', q0, F')
où 2Q est l'ensemble des parties de Q, où l'ensemble de fin F'
vérifie
F' = { Q | Q Ç F ¹ Ø)
et la fonction de transition d' est définie, pour tout aÎ S
et tout E Ì Q, par
Alors on montre facilement que les mots acceptés par A
le sont aussi par l'automate déterministe A'.
Comme vu dans les exemples précédents, le nombre d'états
peut être plus grand dans la version déterministe. En fait, on peut
montrer qu'il peut devenir exponentiel. Le théorème précédent indique
simplement que le non-déterminisme n'introduit pas un nouvel ensemble
de langages reconnus. Toutes les définitions précédentes d'automates
finis sont donc équivalentes.
Nous énonçons deux autres théorèmes sans démonstration.
Théorème 2 [Myhill, Nerode]
Tout langage reconnu par un automate fini est reconnu par un automate
déterministe minimal unique à un isomorphisme près sur le nom des
états.
Ce théorème dit que, pour tout langage reconnu par un automate fini,
il existe un automate déterministe minimal canonique le
reconnaissant. On peut donc déterminiser un automate non-déterministe
et calculer ensuite l'automate minimal correspondant. Remarquons que
le théorème n'est pas vrai pour les automates non-déterministes.
Théorème 3 [Kleene]
Les langages reconnus par un automate fini sont exactement ceux
décrits par les expressions régulières.
Ce théorème, attribué un peu rapidement au promoteur des expressions
régulières, Kleene, connecte la notion d'expression régulière et la
notion d'automates finis. Ainsi les langages reconnus par des
automates finis sont aussi appelés langages réguliers. On
comprend donc mieux les analyseurs lexicaux du
chapitre 2. Les programmes calculant les
lexèmes décrits à partir d'expressions régulières étaient en fait des
implémentations d'un automate fini (déterministe) les calculant. Le
contrôle de ces programmes représentaient les états de cet automate.
La mémoire utilisée pour calculer les lexèmes ne dépassait pas celle
nécessaire pour représenter les états de ces automates; elle était
donc constante, ou encore en O(1).
Exercice 49
Trouver un automate fini non-déterministe de n états dont la version
déterministe a 2n états.
Exercice 50
Montrer que, si on change la définition d'automate fini (déterministe
ou non-déterministe) pour autoriser plusieurs états initiaux, on
reconnait encore le même ensemble de mots.
En 1936, Turing a défini une puissante notion de machine étonnament
simple. Il s'agit de pratiquement la même définition que celle des
automates finis (fonctionnant dans les deux sens), avec une différence
importante: on peut écrire sur la bande de lecture.
Exemple 8 Mots anbn.
Le langage à reconnaitre est l'ensemble des mots de la forme anbn
(n ³ 0). Avec un automate fini, on peut montrer que c'est
impossible. Avec une machine de Turing, on écrit sur la bande pour
compter les nombres relatifs de a et de b. On suppose également
une infinité de caractères blancs B derrière le mot à
reconnaître. La machine de Turing a le fonctionnement suivant: on
remplace le premier a par un X, puis on cherche le premier
b à droite, on le remplace par un Y. On repart à gauche jusqu'à un
X. Si juste à sa droite, on trouve un a, on le remplace à nouveau
par un X et on repart à droite à la recherche d'un b, qu'on
remplace par un Y, puis on repart à gauche. Etc. Si juste à droite
de X, on avait trouvé un Y, on doit s'assurer qu'il n'y a plus que
des Y sur la droite jusqu'au premier caractère blanc. Si c'est le
cas, on accepte le mot; sinon on le refuse. Graphiquement, la
figure 7.10 résume les états successifs que
prend la bande. La tête de lecture est sous la lettre soulignée.
| aaabbb |
| Xaabbb |
| Xaabbb |
| Xaabbb |
| XaaYbb |
| XaaYbb |
| XaaYbb |
|
| XaaYbb |
| XXaYbb |
| XXaYbb |
| XXaYbb |
| XXaYYb |
| XXaYYb |
| XXaYYb |
|
| XXaYYb |
| XXXYYb |
| XXXYYb |
| XXXYYb |
| XXXYYY |
| XXXYYY |
| XXXYYY |
|
| XXXYYY |
| XXXYYY |
| XXXYYY |
| XXXYYYB |
| XXXYYYBB |
|
Figure 7.10 : Etats successifs de la bande d'une machine de Turing
lors de la reconnaissance du mot a3b3.
Plus précisément, une machine de Turing est un 7-uplet M = (Q,
S, G, d, q0,B, F) où:
-
S est un alphabet d'entrée,
- G est un alphabet des symboles de la bande (S
Ì G),
- B Î G - S est le symbole blanc,
- Q est un ensemble fini d'états,
- q0 Î Q est l'état initial,
- F Ì Q est l'ensemble des états de fin,
- d : Q × G ® Q × G × {
gauche, droite } est la fonction de transition.
Le fonctionnement peut se deviner à partir de celui des automates
finis déterministes. Le deuxième résultat renvoyé par d est le
symbole qu'on écrit sous la tête de lecture, avant de faire le
mouvement indiqué par le troisième résultat. La bande de lecture (et
d'écriture) est supposée infinie vers la droite. Elle a une portion
finie à gauche non blanche. A partir d'une certaine case, la
bande est constamment blanche vers la droite. Au début, la machine est
dans l'état q0, la tête de lecture est sur la première lettre d'un mot
w placé sur la partie gauche de la bande. La machine accepte tout
mot dès qu'un état de fin est atteint. (Tous les caractères de w ne
sont pas forcément lus.) Formellement, un configuration est un triplet
(u, q, v) où
-
q Î Q est l'état courant,
- u = X1X2... Xi-1 Î G* est le mot strictement à
gauche de la tête de lecture,
- v = XiXi+1... Xn Î G* est le mot à droite de
la tête de lecture jusqu'au caractère non blanc le plus à droite.
Graphiquement, une configuration est illustrée sur la
figure 7.11.
Figure 7.11 : Configuration d'une machine de Turing.
Les transitions sont définies par la relation binaire suivante sur les
configurations:
| d (q, X) = (q', Y, droite) |
Þ |
(u, q, Xv) ¾® (uY, q', v) |
| d (q, B) = (q', Y, droite) |
Þ |
(u, q, e) ¾® (uY, q', e) |
| d (q, X) = (q', Y, gauche) |
Þ |
(uZ, q, Xv) ¾® (u, q', ZYv) |
| d (q, B) = (q', Y, gauche) |
Þ |
(uZ, q, e) ¾® (u, q', ZY) |
| T(M) = {w | wÎ S*,
(e, q0,w) |
|
(u,q,v), q Î F }
|
Pour l'exemple 8, on considère la machine de
Turing M = (Q, S, G, d, q0,B, F) où S = {a,
b}, G = {a, b, X, Y, B}, Q = {q0, q1, q2, q3, q4 },
q0 est l'état initial, F = { q4 }, et la fonction de transition
d est décrite par le tableau à double entrée suivant:
| |
a |
b |
X |
Y |
B |
| q0 |
(q1,X,droite) |
|
|
(q3,Y,droite) |
|
| q1 |
(q1,a,droite) |
(q2,Y,gauche) |
|
(q1,Y,droite) |
|
| q2 |
(q2,a,gauche) |
|
(q0,X,droite) |
(q2,Y,gauche) |
|
| q3 |
|
|
|
(q3,Y,droite) |
(q4,B,droite) |
| q4 |
|
|
|
|
|
|
Le principe de fonctionnement d'une machine de Turing est donc très
simple: le nombre d'états est fini, on a une fonction de transition
entre ces états avec la bande servant de mémoire annexe. Cela fait une
grande différence par rapport aux automates finis, puisque la taille
mémoire utilisée est a priori non bornée. Dans le cas de anbn, on
se sert d'une mémoire en O(n). Tout le coté fini de la description
d'un calcul est résumé dans les machines de Turing: états, alphabet
d'entrée et de symbole de bande, partie non blanche de la
bande. Pourtant, la programmation avec des machines de Turing est
fastidieuse. Une des raisons provient de l'accès séquentiel aux
données rangées en mémoire (c'est-à-dire sur la bande). On est donc en
droit de se demander si en rajoutant des instructions, on va pouvoir
calculer plus de fonctions et avec plus de confort.
Comme pour les automates finis, on peut écrire la fonction accepter d'acceptation d'un mot w par une machine
M. On remarque qu'à la différence des automates finis, la
bande est maintenant décrite par une chaîne de caractères modifiable de la classe StringBuffer. On note aussi que sa
taille est augmentée dynamiquement grâce à la méthode append
de la classe StringBuffer. On suppose également que cette
opération est toujours possible, et qu'on dispose donc d'une mémoire
de taille non bornée.
class Turing {
final static int GAUCHE = 0, DROITE = 1;
final static char BLANC = 'B';
int q0;
Liste fin;
Action[ ][ ] delta;
static boolean accepter (String w, Turing m) {
StringBuffer bande = new StringBuffer (w);
int tete = 0;
int q = m.q0;
while ( !Liste.estDans(m.fin, q) ) {
char c = tete < bande.length() ? bande.charAt(tete) : BLANC;
Action a = m.delta [q][c];
if (a == null) return false;
q = a.q;
if (a.dept == GAUCHE && tete > 0)
bande.setCharAt(tete--, a.c);
else if (a.dept == DROITE && tete < bande.length())
bande.setCharAt(tete++, a.c);
else if (a.dept == DROITE && tete == bande.length()) {
bande.append(a.c);
++tete;
} else return false;
}
return true;
}
class Action { int q; char c; int dept; } |
Exercice 51
Donner une machine de Turing qui reconnaisse les palindromes
w formés de a et de b tels que w=wR où wR est l'image
miroir de w.
Exercice 52 Trouver une machine de Turing qui reconnaisse les
mots bien parenthésés formés de a et de b.
Exercice 53 Donner une machine de Turing qui calcule le successeur
x+1 de tout nombre binaire x.
Exercice 54 Donner une machine de Turing qui calcule la somme
x+y de tous nombres binaires x et y.
Exercice 55 Soit S(n) le nombre maximal d'étapes pris par
une machine de Turing (déterministe) à n états avant de s'arréter en
partant d'une bande complètement blanche. Calculer S(n) pour
n £ 4 (le castor affairé de Rado).
| 7.6 |
Autres définitions de machines de Turing |
|
Plusieurs définitions alternatives existent pour les machines de
Turing. Nous en considérons quelques unes:
- d : Q × G ® 2 Q × G × {
gauche, droite }
Les machines de Turing non-déterministes peuvent évoluer, dans tout
état, au choix avec plusieurs transitions possibles. Formellement,
| (q', Y, droite) Î d (q, X) |
Þ |
(u, q, Xv) ¾® (uY, q', v) |
| (q', Y, droite) Î d (q, B) |
Þ |
(u, q, e) ¾® (uY, q', e) |
| (q', Y, gauche) Î d (q, X) |
Þ |
(uZ, q, Xv) ¾® (u, q', ZYv) |
| (q', Y, gauche) Î d (q, B) |
Þ |
(uZ, q, e) ¾® (u, q', ZY) |
- Machines de Turing avec la bande infinie à gauche et à droite.
Les transitions sur les configurations sont alors définies par:
| d (q, X) = (q', Y, droite) |
Þ |
(u, q, Xv) ¾® (uY, q', v) |
| d (q, B) = (q', Y, droite) |
Þ |
(u, q, e) ¾® (uY, q', e) |
| d (q, X) = (q', Y, gauche) |
Þ |
(uZ, q, Xv) ¾® (u, q', ZYv) |
| d (q, B) = (q', Y, gauche) |
Þ |
(uZ, q, e) ¾® (u, q', ZY) |
| d (q, X) = (q', Y, gauche) |
Þ |
(e, q, Xv) ¾® (e, q', BYv) |
| d (q, B) = (q', Y, gauche) |
Þ |
(e, q, e) ¾® (e, q', BY) |
- Machines de Turing avec transitions immobiles.
d : Q × G ® Q × G ×
{ gauche, immobile, droite }
Les transitions sont définies par la relation binaire suivante sur les
configurations:
| d (q, X) = (q', Y, droite) |
Þ |
(u, q, Xv) ¾® (uY, q', v) |
| d (q, B) = (q', Y, droite) |
Þ |
(u, q, e) ¾® (uY, q', e) |
| d (q, X) = (q', Y, gauche) |
Þ |
(uZ, q, Xv) ¾® (u, q', ZYv) |
| d (q, B) = (q', Y, gauche) |
Þ |
(uZ, q, e) ¾® (u, q', ZY) |
| d (q, X) = (q', Y, immobile) |
Þ |
(u, q, Xv) ¾® (u, q', Yv) |
| d (q, B) = (q', Y, immobile) |
Þ |
(u, q, e) ¾® (u, q', Y) |
- Machines avec n bandes. M = (Q, S, G,
d, q0,B, F) est construit à partir de n machines
Mk = (Qk, S, G, dk, qk0,B, Fk)
à une seule bande en considérant:
-
Q = Q1 × Q2 × ... Qn,
- d (q1, q2, ... qn) = (d1(q1), d2(q2),
... dn(qn)),
- q0 = q10 × q20 × ... qn0,
- F = F1 × F2 × ... Fn,
Au début, le mot w à droite de la première tête de lecture, et les
autres bandes sont blanches. Une n-configuration est un n-uplet de
configurations (c1, c2, ... cn) où ck est une configuration
de Mk pour 1 £ k £ n. La relation de transition
devient
(c1, c2, ... cn) ¾® (c'1, c'2, ... c'n)
où ck ¾®k c'k et ¾®k est la relation
de transition sur les configurations de Mk.
- Machines de Turing avec transitions composées.
d : Q × G* ® 2 Q × G* ×
{ gauche, droite }
défini sur un sous-ensemble
fini de G*
C'est une machine non déterministe dont les transitions sont
exactement les mêmes que dans le cas non-déterministe en remplaçant
partout X par un mot non vide x Î G+ et Y par un mot y
Î G.
On peut montrer que toutes ces définitions sont équivalentes. Donc si
un mot w est accepté par l'une de ces machines, il l'est aussi par
une machine d'une autre sorte. Ces équivalences sont anecdotiques;
leurs démonstrations sont intéressantes pour apprendre la technique de
manipulation des machines de Turing. Philosophiquement, il apparait
que le modèle de machine de Turing résiste bien aux extensions.
Exercice 56
Ecrire la fonction accepter d'acceptation d'un mot par une
machine de Turing non-déterministe (selon la première définition de
machine non-déterministe).
Exercice 57
Montrer que les 5 définitions de machines de Turing considérées
reconnaissent les mêmes langages.
Dans les années 1920-1930, à la suite des résultats de Gödel,
plusieurs modèles de la calculabilité ont été introduits: le
l-calcul de Church, les fonctions récursives de Kleene, les
machines de Turing, les systèmes de réécritures de Post. Ces modèles,
quoique très différents dans leur présentation, ont tous été montrés
équivalents. Ce qu'on calculait dans le calcul de Church pouvait être
aussi calculé avec les machines de Turing, ou s'exprimait aussi avec
une fonction récursive à la Kleene, et réciproquement. Church a donc
émis le postulat suivant:
Thèse 1 [Church]
Tous les modèles de la calculabilité sont équivalents.
Cette hypothèse, parfois aussi attribuée à Turing (élève de Church),
stipule qu'il y a un modèle unique de la calculabilité. Ce que l'on
peut calculer avec une machine de Turing peut aussi être calculé en
Java sur un PC; tout ce qui peut être calculé sur un PC peut être
calculé sur un Mac; tout ce qu'on peut calculer en Java peut être
aussi calculé en Ocaml, et réciproquement. Quelque soit le langage de
programmation (Java, ML, Ocaml, Ada), on calcule les mêmes fonctions.
Quelquesoit la machine support (PC, Mac, Alpha, HP), on calcule les
mêmes fonctions. Le modèle unique de la calculabilité repose sur des
hypothèses fortes de représentation finie du calcul, et sur rien de
plus.
Pourtant, ce qui est calculé avec un automate fini est strictement
moindre que ce qu'on peut faire avec une machine de Turing. Nous avons
cité l'exemple du langage {an bn | n ³ 0 } reconnaissable
par une machine de Turing, mais pas par un automate fini. Bien d'autres
exemples existent. La raison profonde provient de l'espace mémoire
borné seulement disponible avec un automate fini. En effet, à
partir d'un certain n, il sera impossible de se souvenir du nombre
de a rencontrés dans le mot anbn, et donc impossible de compter
le nombre identique de b. Une machine de Turing dispose d'un espace
mémoire non-borné grâce à sa bande (réinscriptible). C'est cela qui
donne plus de puissance à une machine de Turing.
Traditionnellement, on utilise la thèse de Church en informatique sans
montrer dans les détails qu'un langage de programmation ou un modèle
de machine peut être codé en une machine de Turing. Si le raisonnement
est parfaitement exact au niveau d'un langage de programmation
puisqu'on peut toujours le compiler vers du code exécutable par une
machine de Turing, on peut plus douter de l'argument pour comparer un
ordinateur moderne à une machine de Turing. Un ordinateur dispose-t-il
d'une mémoire non bornée? Les réponses peuvent diverger: les
pragmatiques diront que la mémoire centrale est bornée, les idéalistes
diront qu'on peut toujours rajouter de la mémoire externe (disques,
bandes), autant que nécessaire, les ultra-sceptiques diront que le
nombre d'atomes de l'univers est borné et qu'on ne peut donc disposer
d'une mémoire arbitrairement grande. En règle générale, s'il est vrai
qu'on peut comparer un ordinateur à un automate fini, le nombre
d'états sera très grand et une bonne approximation consiste à prendre
le modèle d'une machine de Turing.
Exercice 58
Montrer qu'une machine de Turing qui n'écrit que sur une partie bornée
de la bande est équivalente à un automate fini.
Si nous avons vu qu'un modèle très simple suffisait pour faire tous
les calculs imaginables, il n'est absolument pas garanti que
l'écriture de programmes soit commode dans le modèle simplifié. Au
contraire, on a besoin de langages de programmation de haut-niveau
pour avoir une écriture plus concise. Par ailleurs, on peut se
demander si on sait calculer toute fonction des mathématiques, ou s'il
existe des fonctions non-calculables.
Depuis Gödel, nous savons qu'il existe des objets
non-calculables. Un argument savant consiste à dire qu'il existe un
nombre dénombrable (À0) de machines de Turing, alors qu'il y a
un bien plus grand nombre (À1) de langages sur l'alphabet
S. Un tout simple argument par diagonalisation donne ausi la
solution. Comme les programmes ont une description finie, on peut
les énumérer, c'est-à-dire trouver une fonction f de N
dans les machines de Turing tel que f(i) = Mi est la
i-ème machine de Turing. De même, on peut énumérer tous les mots sur
un alphabet S avec une fonction y(i) = wi est le i-ème
mot. On peut donc parler de la i-ème machine et du i-ème mot.
Considérons l'ensemble
L = { wi | wi ÏT(Mi) }
Alors L ne peut être reconnu par une machine de Turing. Sinon, il
existerait une machine Mk telle que L =
T(Mk), et on aurait wk Î T(Mk) si et
seulement si wk ÏT(Mk). Contradiction.
Théorème 4 [Gödel]
Il existe des langages non reconnaissables par une machine de Turing.
Supposons que nous disposions d'une représentation n pour tout
entier naturel n. Par exemple, n sera la chaîne de caractères en
représentation décimale donnée par l'expression Integer.toString(n) de Java. On peut alors parler de fonctions
calculables sur N par machines de Turing. En effet, nous
considérerons les fonctions fi définies par
| fi(n) = m ssi
(e, q0, |
|
) |
|
( |
|
,q,v) (q Î F) |
|
static int f (int n) { ... } |
(en se restreignant aux arguments et résultats positifs). A nouveau,
il existe plein de fonctions de N dans N non calculables,
puisque le nombre de programmes écrits en Java est dénombrable. Plus
généralement, on peut aussi définir des fonctions calculables sur
d'autres domaines que N, mais la théorie demande plus d'habileté.
Exercice 59
Montrer rigoureusement qu'il existe des fonctions sur N non
calculables.
| 7.8 |
Indécidabilité de l'arrêt |
|
Parmi les fonctions non calculables, la fonction décidant de l'arrêt
est célèbre. Il s'agit de tester si une machine M s'arrête
avec un mot w donné sur la bande dans l'état initial. Pour les
fonctions calculables, cela revient à trouver si f(n) est défini
pour un n donné. Turing a montré que c'était impossible. Faire la
démonstration avec les machines de Turing est un peu délicate, car
faisant appel à des notions avancées de la théorie de la
calculabilité. Nous en considérons une version simplifiée sur des
programmes Java.
Ecrivons e ¯ et e' pour signifier que
l'évaluation de l'expression e termine et que celle de e' ne
termine pas. Supposons qu'il existe une fonction termine qui
prend un objet o en argument et teste si sa méthode f (sans
arguments) termine. On a donc
| Turing.termine(o) =
|
ì
í
î |
| true si o.f( ) ¯ |
| false si o.f( ) |
|
|
class Turing {
static boolean termine (Object o) {
// La valeur retournée vaut true si o.f()
// termine. Sinon la valeur retournée vaut false.
// (le code n'est pas public car breveté par le vendeur)
} }
class Facile {
void f () { }
}
class Boucle {
void f () {
for (int i = 1; i > 0; ++i)
;
} }
class Absurde {
void f () {
while (Turing.termine(this))
;
} }
class Test {
public static void main (String[ ] args) {
Facile o1 = new Facile();
System.out.println (Turing.termine(o1));
Boucle o2 = new Boucle();
System.out.println (Turing.termine(o2));
Absurde o3 = new Absurde();
System.out.println (Turing.termine(o3));
} } |
Pour o3 le problème est plus complexe. En effet
| Turing.termine(o3) = true
ssi
o3.f() ¯
ssi
Turing.termine(o3) = false |
Théorème 5
Il n'existe pas de fonction calculable h telle que pour tout i et
n, on a h(i, n) = 1 si fi(n) est défini, et h(i, n) = 0 si
fi(n) n'est pas défini.
La théorie de la calculabilité est amusante. Elle apporte
principalement des résultats d'impossibilité. Il y a pourtant quelques
résultats positifs. En voici un donné en exercice.
Exercice 60
Trouver un programme auto-reproductible en Java, c'est-à-dire un
programme dont le résultat (par impression sur la sortie) est son
propre code.
| 7.9 |
Applications des automates finis à la concurrence |
|
Parmi les applications des automates finis, un certain nombre d'entre
elles consistent à faire des vérifications, principalement de
programmes concurrents, par méthode exhaustive (encore dénommé model checking en anglais). Si ces méthodes sont parfois peu
esthétiques, elles sont souvent beaucoup plus efficaces que d'autres
méthodes de correction de programmes, utilisant la logique ou les
méthodes formelles. Toutefois, elles se prêtent moins à la
paramétrisation (et donc à la modularité) des preuves de correction.
 |
|
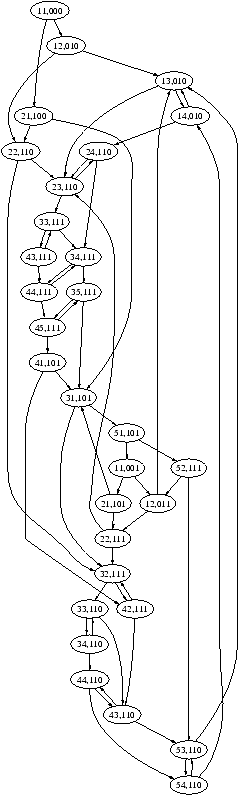
| Dans l'algorithme de Peterson, une configuration est représentée par
le quintuplet (p, p', actif[0], actif[1], tour) où p est le
compteur ordinal dans le premier programme, p' est celui du deuxième
programme, et actif[0], actif[1], tour sont les valeurs des
variables de synchronisation. Il y a 5 points possibles dans le code
de chacun des processus: pour t0, alors p=1 correspond au début
du code, p=2 est le point du programme avant de mettre actif[0] à
vrai (1 ici dans notre codage), p = 3 est le point du programme
avant le test de actif[1], p=4 est le point avant le test du
tour, p=5 est la section critique avant de remettre actif[0] à
faux et de retourner en p=1; pour t1, alors p' prend les
valeurs symétriques. La fonction de transition de l'automate est
décrite ci-dessous. A chaque état, deux transitions sont possibles
selon que le processus t0 ou t1 s'exécute. On vérifie sur
l'automate de gauche qu'on n'atteint jamais un état de la forme
((
5 5, - - -)). |
|
| |
| L'automate complet a 25 × 8 = 200 états. Nous n'avons dessiné
que les états accessibles depuis ((
1 1, 0 0 1)). |
|
| |
| |
(
1 -, - - -) |
® |
(
2 -, 1 - -) |
| |
(
2 -, - - -) |
® |
(
3 -, - - 1) |
| |
(
3 -, - 0 -) |
® |
(
5 -, - 0 -) |
| |
(
3 -, - 1 -) |
® |
(
4 -, - 1 -) |
| |
(
4 -, - - 0) |
® |
(
5 -, - - 0) |
| |
(
4 -, - - 1) |
® |
(
3 -, - - 1) |
| |
(
5 -, - - -) |
® |
(
1 -, 0 - -) |
| |
|
| |
(
- 1, - - -) |
® |
(
- 2, - 1 -) |
| |
(
- 2, - - -) |
® |
(
- 3, - - 0) |
| |
(
- 3, 0 - -) |
® |
(
- 5, 0 - -) |
| |
(
- 3, 1 - -) |
® |
(
- 4, 1 - -) |
| |
(
- 4, - - 1) |
® |
(
- 5, - - 1) |
| |
(
- 4, - - 0) |
® |
(
- 3, - - 0) |
| |
(
- 5, - - -) |
® |
(
- 1, - - -) |
|
|
Figure 7.12 : Vérification par méthode exhaustive de l'algorithme de Peterson.
Exemple 9 Vérification de l'algorithme de Peterson.
Souvent la correction de programmes concurrents se ramène à l'étude
d'un nombre fini de cas, que l'on peut caractériser par un automate
fini. C'est le cas de l'algorithme de Peterson considéré
en 6.8 où l'exclusion des sections critique est
caractérisée par l'inaccessibilité de certains états, comme expliqué
sur la figure 7.12.
Nous considérons à présent deux protocoles d'échanges de messages sur
les réseaux. Ces exemple sont un peu plus longs à expliquer. En fait
il ne sont pas si éloignés de l'exemple précédent. Il s'agit
d'échanger de manière sure des messages à travers un réseau. Nous
considérons deux protocoles: un simple contrôle de flux et le protocole
du bit alterné, dans le cas d'une liaison uni-directionnelle.
Exemple 10 Protocole réseau: contrôle de flux.
Deux processus évoluent en parallèle reliés par un canal de
communication. Le premier, l'émetteur, envoie sans cesse des messages
m0, m1, m2, ... sur le canal à destination du deuxième
processus, le récepteur, qui lit continument ces messages. Les deux
processus doivent suivre un protocole de contrôle de flux pour éviter
que le récepteur ne soit submergé une multitude de messages.
L'émetteur émet un message (action !m), puis attend un accusé de
réception envoyé par le lecteur (action ?a). Il peut alors
recommencer à émettre un nouveau message à destination du lecteur. Le
fonctionnement à deux états de l'émetteur est représenté à gauche sur
la figure 7.13. Le processus de lecture lui
attend un message émis par l'émetteur. Il le lit (action ?m), puis
émet un accusé de réception vers l'émetteur (action !a). Il revient
à l'attente de lecture du prochain message. Son fonctionnement est au
centre sur la figure 7.13. Le système en
entier, constitué de l'émetteur et du récepteur et du contenu du canal
de communication, est résumé à droite sur la
figure 7.13. Il a 4 états XYZ où X est
l'état de l'émetteur, Y celui du récepteur, Z est le contenu du
canal de communication, e signifie action de l'émetteur, r
signifie action du récepteur.
Figure 7.13 : L'automate d'un simple contrôle de flux sur un réseau. (i)
à gauche: l'émetteur; (ii) au centre: le récepteur; (iii) à
droite: le système en entier
Le contrôle de flux est proche du contrôle considéré dans les files
concurrentes vu en 6.5 ou encore dans le problème du
producteur-consommateur
de 6.10. Toutefois, il n'y a pas de
mémoire commune pour assurer la communication; il faut envoyer des
messages de l'émetteur au récepteur et réciproquement pour assurer la
synchronisation.
Exemple 11 Protocle réseau: protocole du bit alterné.
Le protocole précédent suppose qu'aucun message ne puisse se
perdre. Or, les pertes de messages sont fréquentes sur un réseau (à un
certain niveau de protocole). Il faut donc considérer le cas où le
message mi émis se perd, alors le récepteur ne reçoit rien et ne
peut envoyer d'accusé de réception. L'émetteur doit ré-émettre le
message mi au bout d'un certain temps (time-out
), jusqu'au
moment où l'accusé de réception lui parvienne. Mais, il se peut que
l'accusé de réception se perde aussi, et alors le récepteur va lire
deux fois le même message mi. Pour éviter la duplication de la lecture
d'un même message, le protocle du bit alterné consiste à utiliser un
bit pour caractériser le message émis, et mettre le récepteur dans un
mode où il attend un certain type de message pour lecture
effective. Sur la figure 7.14, on trouve en haut à
gauche l'automate décrivant le protocole de l'émetteur, en haut à
droite celui du récepteur, en bas l'automate de tout le système
(émetteur, récepteur, état du canal de communication). Chaque état
XYZ de ce dernier automate est donné par l'état X de l'émetteur,
l'état Y du récepteur, et le contenu Z du canal; l'action e veut
dire action de l'émetteur, r veut dire action du récepteur, t veut
dire dépassement de temps.
Figure 7.14 : L'automate du protocole du bit alterné sur une liaison
uni-directionnelle. (i) en haut à gauche: l'émetteur; (ii) en
haut à droite: le récepteur; (iii) en bas: le système en entier.
Dans l'état 0, l'émetteur envoie un message de type 0 et passe
dans l'état 1. Dans l'état 1, l'émetteur attend un accusé de
réception. S'il arrive, on le lit et l'émetteur passe à l'état 2. Si
un dépassement de temps se produit, l'émetteur revient à l'état 0.
Dans l'état 2, l'émetteur envoie un message de type 1 et passe
dans l'état 3. Là, il attend un accusé de réception. S'il arrive,
il le lit et passe dans l'état 0. Si un dépassement de temps se
produit, l'émetteur revient à l'état 2.
Coté récepteur, au début, on est dans l'état 0. Le récepteur attend
alors un message de type 0. S'il arrive, on le lit et on va à l'état
1. Si c'est un message de type 1 qui arrive, c'est un message dû à
une ré-émission causée par un dépassement de temps, on le saute et on
passe à l'état 3. Dans l'état 3, le récepteur émet un accusé de
réception et passe à l'état 0. Dans l'état 1, après la lecture
d'un message effectif de type 0, on émet un accusé de réception et
on passe à l'état 2. Dans l'état 2, on attend un message de type
1 et on va à l'état 3. Si c'est un message de type 0 qui arrive,
cela veut dire que c'est un message ré-émis dû à un dépassement de
temps, on saute le message, et on revient à l'état 1 pour
re-émettre un accusé de réception.
Sur l'automate du système tout entier, on voit comment le système
évolue dans le temps en faisant progresser concurremment les deux
automates de l'émetteur et du récepteur. Dans l'état XYZ, l'émetteur
émet un message de type ë X/2 û, le récepteur est en
attente d'un message de type ë Y/2 û. On vérifie donc
qu'on ne lit jamais deux fois le même message mi, puisqu'il est lu
la première fois, et sauté s'il est réémis. En fait le lecteur lit
mi sur la transition de 100 à 11- et mi+1 sur la
transition de 321 à 33-. L'émetteur lit l'accusé de réception sur
les transitions de 12a à 22- et de 30a à 00-. Toutes les
autres lectures de messages ou d'accusés de réception sont dues à des
réémissions.
Le protocole du bit alterné a en fait une belle structure symétrique
qui permet de le généraliser à des canaux de communication
bi-directionnels. En outre, au lieu d'assurer le passage d'un seul
message, on peut avoir un protocole sur une fenêtre de plusieurs
messages, ce qui permet d'accélérer les vitesses de transmissions. Les
automates de ces protocoles à fenêtres ont un bien plus grand nombre
d'états.
Une toute autre classe d'exemples d'automates finis décrivant des
fonctionnements concurrents est celle des automates cellulaires. Les
automates cellulaires sont des automates finis dont on suppose les
fonctionnements synchronisés par une même horloge. Le prototype
des automates cellulaires est celui du jeu de la vie de Conway. Un
exemple plus militaire est celui du peloton d'exécution, laissé en
exercice (difficile).
Exercice 61 Le peloton d'exécution.
Il y a une forte brûme et un vent violent ce matin sur le plateau. On
ne voit rien, on n'entend rien. Le général convoque n-1 soldats,
les aligne sur son coté, et veut les faire tirer tous en même temps.
Le général et les soldats sont des machines synchrones. Ils réagissent
tous en phase en ne tenant compte que des états de leurs deux voisins
de gauche ou de droite. Il y a 3 types de machines: le général qui
n'a qu'un seul voisin (le premier soldat), les soldats, le soldat en
bout de chaîne qui n'a aussi qu'un seul voisin. Montrer qu'il existe
une solution, avec un nombre fini d'états, indépendant de n, pour
chaque machine. (Indication: supposer n=2k et trouver le soldat du
milieu)