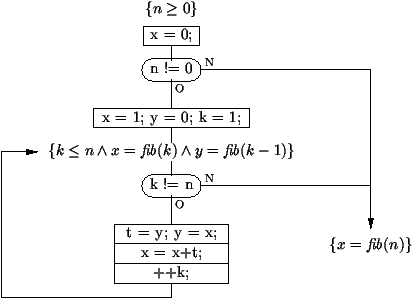
Figure 5.1 : Organigramme d'un programme avec ses invariants



|
|
|
int fib (int n) { int[ ] tab = new int[n+1]; tab[0] = 0; tab[1] = 1; for (int i = 2; i <= n; ++i) tab[i] = tab[i-2] + tab[i-1]; return t[n]; } |
|
static int fibonacci (int n) { int x = 0; if (n != 0) { x = 1; int y = 0; for (int k = 1; k != n; ++k) { int t = y; y = x; x = x + t; } } return x; } |
|
static int fibonacci (int n) { // P= {n ³ 0} int x = 0; if (n != 0) { x = 1; int y = 0; for (int k = 1; k != n; ++k) { int t = y; y = x; x = x + t; } } // Q= {x = fib(n)} return x; } |
Figure 5.1 : Organigramme d'un programme avec ses invariants
|
static int fibonacci (int n) { // P= {n ³ 0} int x = 0; if (n != 0) { x = 1; int y = 0; int k = 1; // I = {k £ nÙ x = fib(k)Ù y = fib(k-1)} while (k != n) { int t = y; y = x; x = x + t; ++k; } } // Q= {x = fib(n)} return x; } |
|
static int fibonacci (int n) { {n ³ 0} int x = 0; if (n != 0) { x = 1; int y = 0; int k = 1; {k £ nÙ x = fib(k)Ù y = fib(k-1)} while (k != n) { int t = y; y = x; x = x + t; ++k; } } {x = fib(n)} return x; } |
|
1 static int fibonacci (int n) { 2 {n ³ 0} 3 int x = 0; 4 {n ³ 0 Ù x = 0} 5 if (n != 0) { 6 x = 1; int y = 0; 7 {n > 0Ù x = fib(1)Ù y = fib(0)} 8 int k = 1; 9 {0 < k £ nÙ x = fib(k)Ù y = fib(k-1)} 10 while (k != n) { 11 {0 < k < nÙ x = fib(k)Ù y = fib(k-1)} 12 int t = y; 13 {0 < k < nÙ x = fib(k)Ù y = fib(k-1) Ù t = fib(k-1) } 14 y = x; 15 {0 < k < nÙ x = fib(k)Ù y = fib(k) Ù t = fib(k-1) } 16 x = x + t; 17 {0 < k < nÙ x = fib(k+1)Ù y = fib(k) Ù t = fib(k-1) } 18 ++k; 19 } 20 {k = nÙ x = fib(k)Ù y = fib(k-1)} 21 } 22 {x = fib(n)} 23 return x; 24 } |
|
static int pgcd (int a, int b) { int x = a, y = b; while (x != y) if (x > y) x = x - y; else y = y - x; return x; } |
|
1 static int pgcd (int a, int b) { 2 {a > 0 Ù b > 0} 3 int x = a, y = b; 4 {x > 0 Ù y > 0 Ù pgcd(x,y) = pgcd(a,b)} 5 while (x != y) { 6 {x > 0 Ù y > 0 Ù x¹ y Ù pgcd(x,y) = pgcd(a,b)} 7 if (x > y) { 8 {x > 0 Ù y > 0 Ù x > y Ù pgcd(x-y,y) = pgcd(a,b)} 9 x = x - y; 10 {x > 0 Ù y > 0 Ù pgcd(x,y) = pgcd(a,b)} 11 } else { 12 {x > 0 Ù y > 0 Ù x < y Ù pgcd(x,y-x) = pgcd(a,b)} 13 y = y - x; 14 {x > 0 Ù y > 0 Ù pgcd(x,y) = pgcd(a,b)} 15 } 16 } 17 {x > 0 Ù x = y = pgcd(x,y) = pgcd(a,b)} 18 return x; 19 } |
|
static int pgcd (int a, int b) { int x = a, y = b; while (y != 0) { int r = x % y; x = y; y = r; } return x; } |
|
Figure 5.2 : Le drapeau hollandais
|
static void drapeauHollandais (int[ ] a) { int b = 0, i = 0, r = a.length; while (i < r) { switch (a[i]) { case BLEU: int t = a[b]; a[b] = a[i]; a[i] = t; ++b; ++i; break; case BLANC: ++i; break; case ROUGE: --r; int u = a[r]; a[r] = a[i]; a[i] = u; break; } } } |
|
static void drapeauHollandais (int[ ] a) { int b = 0, i = 0, r = a.length, n = r; {f(0,b,BLEU) Ù f(b,i,BLANC) Ù f(r,n,ROUGE)} while (i < r) { switch (a[i]) { case BLEU: {f(0,b,BLEU) Ù f(b,i,BLANC) Ù f(r,n,ROUGE) Ù a[i] = BLEU} int t = a[b]; a[b] = a[i]; a[i] = t; {f(0,b+1,BLEU) Ù f(b+1,i+1,BLANC) Ù f(r,n,ROUGE)} ++b; ++i; break; case BLANC: {f(0,b,BLEU) Ù f(b,i+1,BLANC) Ù f(r,n,ROUGE)} ++i; break; case ROUGE: {f(0,b,BLEU) Ù f(b,i,BLANC) Ù f(r,n,ROUGE) Ù a[i] = ROUGE} --r; {f(0,b,BLEU) Ù f(b,i,BLANC) Ù f(r+1,n,ROUGE) Ù a[i] = ROUGE} int u = a[r]; a[r] = a[i]; a[i] = u; break; } } {f(0,b,BLEU) Ù f(b,r,BLANC) Ù f(r,n,ROUGE)} } |
|
x = E;
{P(x)}
if (E) S else S'
{Q} S
{Q}
et
{P Ù ¬ E}
S'
{Q} while (E) S
{Q}
S
{I}
S
{Q}
S
{Q'}
Q' Þ Q
La logique de Hoare manipule des assertions dans les programmes. Ces assertions sont censées être vérifiées à chaque fois que le programme passe par leurs emplacements. Mais rien ne garantit que le programme passe à un emplacement donné. Ainsi quand on écrit {P} S {Q}, on sait que si on démarre l'instruction S avec l'assertion P vraie, alors l'assertion Q est vérifiée si on termine S. Mais on n'a aucune garantie sur la terminaison de S. Donc la correction d'un programme par la méthode des assertions, vue jusqu'à présent, dit que l'assertion de fin est vraie si on démarre avec l'assertion de départ également vraie; mais il n'est pas sûr que le programme termine. Par exemple
{P (E)} x = E;{P(x)}
{P Ù E} S {Q} {P Ù ¬ E} S' {Q}
{P} if (E) S else S' {Q}
{P} S{Q} {Q}S'{R}
{P} S S'{R}
{P} S{Q}
{P} \{S\}{Q}
{P Ù E} S{P}
{P} while (E) S{P Ù ¬ E}
P Þ P' {P'} S{Q'} Q' Þ Q
{P} S{Q}
Figure 5.3 : Logique de Floyd-Hoare
while (true) S; {P}
|
assert, qui lève une
erreur si l'assertion n'est pas vérifiée. On retrouve aussi cette
instruction en Caml, C, C++. En Java 1.1.8, il n'y a pas de système
d'assertions, mais il est toujours possible d'écrire sa propre classe.|
class AssertionError extends Error { } public class Assertion { public static void check (boolean e) { if (!e) throw new AssertionError(); } } |
Assertion.check une
expression booléenne quelconque correspondant à l'assertion à tester.
Bien sûr, pour les assertions avec des quantificateurs universels ou
existentiels sur des espaces infinis, c'est plus délicat (quelquesoit
le langage de programmation!).
|
|
static int fact (int n) { int r; if (n == 0) r = 1; else r = n * fact(n-1); return r; } |
|
static int fact (int n) { int r; {n ³ 0 Ù " k. k ³ 0 Þ fact(k) = k! } if (n == 0) r = 1; else r = n * fact(n-1); {r = n!} return r; } |
|
1 static int fact (int n) { 2 int r; 3 {n ³ 0 Ù " k. k ³ 0 Þ fact(k) = k! } 4 if (n == 0) { 5 {n = 0 } 6 r = 1; 7 {n = 0 Ù r = 1 = 0!} 8 } else { 9 {n-1 ³ 0 Ù fact(n-1) = (n-1)! } 10 r = n * fact(n-1); 11 {r = n (n-1)! = n! } 12 } 13 {r = n!} 14 return r; 15 } |
x=f(n);
{P} quand f est définie par:
static int f(int n) { return f(n);}.
|
static Liste inserer (int x, Liste a) { int r; if (a == null || x < a.val) { r = new Liste(x, a); } else if (a.val < x) { r = new Liste(a.val, inserer(x, a.suiv)); } else r = a; return r; } |
| ens(a) = |
ì í î |
|
|
1 static Liste inserer (int x, Liste a) { 2 int r; 3 { ord(a) Ù " a." x. ord(a) Þ ord(inserer(x,a)) Ù " a." x. ens(inserer(a,x)) Ì {x} È ens(a) } 4 if (a == null || x < a.val) { 5 {ord(a) Ù (a ¹ null Þ x < a.val) } 6 r = new Liste(x, a); 7 {ord(r) Ù ens(r) = {x} È ens(a) } 8 } else if (a.val < x) { 9 {ord(a) Ù a ¹ null Ù a.val < x Ù ord(inserer(x,a.suiv)) Ù ens(inserer(x,a.suiv)) Ì {x} È ens(a.suiv) } 10 r = new Liste(a.val, inserer(x, a.suiv)); 11 {ord(r) Ù ens(r) Ì { x } È ens(a)} 12 } else { 13 { ord(a) } 14 r = a; 15 {ord(r) Ù ens(r) = ens(a)} 16 } 17 {ord(r) Ù ens(r) Ì {x} È ens(a)} 18 return r; 19 } |
|
|
static int fibonacci (int n) { {n ³ 0} int x = 0; if (n != 0) { x = 1; int y = 0; int k = 1; {W(n,k) = n - k Ù n ³ k} while (k != n) { int t = y; y = x; x = x + t; ++k; } } {x = fib(n)} return x; } |
|
static int pgcd (int a, int b) { {a > 0 Ù b > 0} int x = a, y = b; {x > 0 Ù y>0 Ù W(x,y) = max(x,y)} while (x != y) if (x > y) x = x - y; else y = x - y; return x; } |
| (i) | ¬ (x < x) | ||
| (ii) | x < y < z Þ x < z |
| (x, y) <l(x',y') | si | x<x' Ú (x=x' Ù y<y') |
| (x, y) <m (x',y') | si | (x1,y1) <l(x1',y1') |
|
static int ack (int m, int n) { {m ³ 0 Ù n ³ 0 Ù W(m,n) = (m,n)} if (m == 0) return n + 1; else if (n == 0) return ack (m - 1, 1); else return ack (m - 1, ack (m, n - 1)); } |
|
static int f (int x) { if (x > 100) return x-10; else return f(f(x+11)); } |


