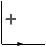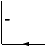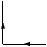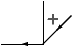Interprétation tridimensionnelle de dessins 2D

Sujet proposé par Philippe Chassignet

`Philippe.Chassignet@polytechnique.fr`

Ce sujet est inspiré de l'ouvrage de Sugihara [1].

1 Préambule

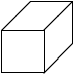
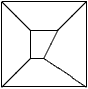
On se donne un dessin 2D, défini comme un ensemble de segments, et on veut en déduire la structure 3D d'une scène de polyèdres dont le dessin serait une vue projective (de paramètres inconnus). Par exemple, on interprète immédiatement le dessin ci-dessous comme la vue¹ d'un cube. Pourtant, nous verrons plus loin qu'il existe des variantes de cette interprétation.

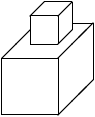
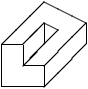
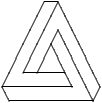
Voici d'autres exemples, pour lesquels l'interprétation est moins triviale ou impossible.

Dans ce projet, on va s'intéresser à l'énumération de l'ensemble des interprétations possibles pour un dessin donné. Nous nous limiterons au cas de solides triédraux mais la méthode peut être généralisée.

2 Détail du sujet

2.1 Prétraitement des segments

Les segments seront lus dans un fichier au format suivant :

n
x₁₁	y₁₁	x₁₂	y₁₂
· · ·
x_n1	y_n1	x_n2	y_n2

où la première ligne indique le nombre de segments et chaque ligne suivante fournit les coordonnées des deux extrémités d'un segment. Ce format est assez représentatif de ce que peut fournir un traitement d'image ou un programme de dessin et il peut contenir des imperfections dans les coordonnées.

La première étape consiste donc à en déduire une description de graphe planaire qui explicite des noeuds et des segments joignant ces sommets. On doit alors identifier des coordonnées (x,y) et (x',y') jugés suffisamment voisines pour correspondre à un même noeud. On admettra que les segments ne se touchent que par leurs extrémités, notamment, il n'y a pas de croisement et un T est décrit comme la jonction de 3 segments.

2.2 Étiquetage des segments

En référence à une interprétation 3D particulière, chaque segment de la figure peut être considéré comme la projection d'une arête concave (segment étiqueté -), d'une arête convexe (segment étiqueté +) ou d'une arête occultante. Une arête occultante est une arête convexe dont on ne voit pas l'une des faces adjacentes. Il y a alors discontinuité de la profondeur de la scène de part et d'autre du segment. Un tel segment doit être orienté et il sera étiqueté par une flèche (ou < , >), avec la convention que la moindre profondeur se trouve à droite dans le sens de la flèche.

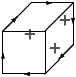
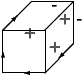
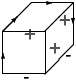
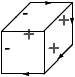
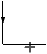
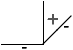
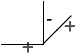
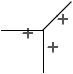
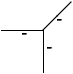
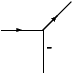
Voici quatre étiquetages de la figure du cube, la première correspond à l'interprétation naturelle d'un cube ``flottant''. Dans les trois autres, le cube est ``collé'' à un plan de fond par l'une de ses faces cachées.

Pour une figure à n segments, il y aurait a priori 4ⁿ étiquetages possibles. Mais la réalisabilité 3D impose des contraintes.

2.3 Étiquetage des noeuds

En fonction des angles d'incidence des segments, on distingue plusieurs types de noeuds. Par exemple, sur la figure du cube, on trouve trois V, trois W et un Y. On caractérise les noeuds de la manière suivante :

- noeuds V, la troisième arête du trièdre est invisible,

- noeuds W, les trois arêtes du trièdre sont visibles, les segments sont dans un même demi-plan,

- noeuds Y, les trois arêtes du trièdre sont visibles, les segments ne sont pas dans un demi-plan,

- noeuds T, il ne s'agit pas de la projection d'un trièdre.

Un noeud T n'existe que dans la décomposition du dessin et il n'est pas la projection d'un sommet 3D. Les deux segments formant la barre horizontale du T sont colinéaires et correspondent à la projection d'une même arête 3D occultante. La barre verticale correspond à une arête qui passe derrière. Un T ne peut donc pas être la forme limite d'un W ou d'un Y. Si c'était le cas, on admet qu'un petit changement du point de vue aurait permis d'avoir un W ou un Y.

En fait, pour chaque forme de noeud, V, W, Y ou T, il n'y a que quelques combinaisons d'étiquetages des segments incidents qui peuvent correspondre à une interprétation projective. Les voici toutes, à une rotation près :

Après avoir identifié la forme de chaque noeud et ordonné ses segments incidents, on peut donc lui associer un ensemble d'étiquetages possibles.

2.4 Énumération des étiquetages globalement cohérents

La cohérence globale d'un étiquetage revient à vérifier que l'étiquetage de chaque noeud détermine la même étiquette aux deux extrémités de chaque segment. On commencera par programmer une recherche ``en force'' qui examine toutes les combinaisons sommet par sommet.

Pour réduire la complexité de cette exploration combinatoire, on peut procéder par relaxation. Cela consiste à regarder si l'ensemble des étiquetages possibles pour un noeud exclut certaines étiquette pour un segment. Par exemple, le segment central d'un W ne peut pas être une flèche. Dans ce cas, cela permet peut-être de supprimer des étiquetages pour le noeud extrémité, on devra alors regarder ce que cela implique pour ses voisins, ...On procède itérativement en gérant convenablement l'ensemble des noeuds qui doivent être examinés.

Cet algorithme converge naturellement et sa complexité globale est linéaire dans le nombre de sommets, donc relativement peu coûteuse. La recherche exhaustive reste nécessaire pour énumérer tous les étiquetages possibles mais elle travaille sur un domaine beaucoup plus petit.

3 Travail demandé

Pour ce projet, il s'agira donc de programmer les étapes de traitement décrites ci-dessus. La réalisation du prétraitement peut être différée dans la mesure où l'on dispose d'une description explicite du graphe. Pour analyser les résultats, on devra également produire la représentation graphique d'une figure étiquetée. On se contentera de programmer un graphisme rudimentaire ou alors on sortira le résultat dans un format reconnu par un utilitaire graphique existant.

Des fichiers au format ``segments'' et au format ``graphe'' pour les dessins de cet énoncé et quelques autres seront disponibles sur le serveur de l'enseignement.

4 Extension possible

L'extension logique consiste à reconstruire, si c'est possible, une structure spatiale tridimensionnelle pour chaque étiquetage.

Il faut commencer par identifier dans le graphe les circuits minimaux qui forment les contours des différentes parties visibles de la scène 3D. Pour les construire, il faut choisir un sens de parcours, par exemple le sens trigonométrique, et procéder à un parcours en profondeur un peu particulier. À chaque noeud, on suit le premier arc non encore utilisé que l'on rencontre en faisant le ``tour'' du noeud dans le sens choisi. On remarquera que tous les cycles minimaux sont parcourus dans le même sens et que l'algorithme produit également, à un moment ou à un autre, le tour extérieur, en sens inverse, de chaque composante connexe. Ce tour sera attaché au fond de la scène 3D. Finalement, chaque segment de la figure est parcouru exactement deux fois, une fois dans chaque sens.

Les profondeurs des sommets 3D sont les inconnues principales du problème de reconstruction. Elles sont liées par un certain nombre d'équations qui expriment que les faces sont planes et d'autres équations ou inéquations qui traduisent l'étiquetage des segments. Lorsque le système admet des solutions, il convient de fixer un nombre prévisible de degrés de liberté pour obtenir une représentation 3D particulière. Le système peut ne pas admettre de solution, cela peut provenir d'une erreur de placement des noeuds, auquel cas on pourrait envisager de corriger le dessin. Dans d'autre cas, c'est structurellement impossible et la réalisation de l'objet implique nécessairement des surfaces gauches.

Pour corriger un dessin, Sugihara propose une méthode basée sur un calcul de flot dans un graphe des contraintes qui permet de décider quels sommets doivent être déplacés et quelles équations déterminent leurs nouvelles positions.

Les élèves intéressés par ces extensions contacteront Philippe Chassignet pour obtenir plus de détails.

Références

[1]: K. Sugihara, Machine Interpretation of Line Drawings, MIT Press, 1986.

1: On a utilisé une perspective cavalière pour des commodités de dessin, mais que le problème est le même pour les ``vraies'' perspectives (avec points de fuite).

Ce document a été traduit de L^AT_EX par H^EV^EA.