Gestion de projet à contraintes de ressources

Sujet proposé par Philippe Baptiste

`baptiste@lix.polytechnique.fr`

1 L'ordonnancement

Ordonnancer, c'est organiser l'exécution de travaux au moyen d'un ensemble de ressources, disponibles en quantité limitée. En pratique, on rencontre de tels problèmes:

dans les systèmes informatiques, lorsque plusieurs activités (ou processus) doivent être exécutées par un ou plusieurs processeurs ;
dans les systèmes de production manufacturière, où des ordres de fabrication correspondant à des produits à réaliser doivent être séquencés sur les différentes machines d'un atelier ;
en gestion de projets (dans les secteurs du bâtiment et des activités de services) décomposables en activités utilisant des ressources partageables.

En raison de son impact sur la productivité, la qualité ou la rapidité de service, on constate pour l'ordonnancement une forte demande en systèmes d'aide à la décision ou bien en algorithmes de résolution, selon le secteur considéré.

2 Le RCPSP

Le problème de gestion de projet à contraintes de ressources (Resource Constrained Project Scheduling Problem, RCPSP) est un problème très général qui recouvre un grand nombre de situations ``classiques'' d'ordonnancement.

Le RCPSP peut être décrit comme suit : n activités A₁, ..., A_n de durées p₁, ..., p_n doivent être ordonnancées sur m ressources R₁, ..., R_m. Une ressource R_u est constituée de K_u machines rigoureusement identiques. On dit aussi que K_u est la capacité de R_u. Pour chaque activité A_i et chaque ressource R_u la consommation k_i,u représente le nombre de machines de la ressource R_u utilisées par A_i entre sa date de début et sa date de fin. Bien entendu, à tout instant t, la capacité d'une ressource doit rester supérieure ou égale au nombre total de machines utilisées par les activités qui sont en cours d'exécution à t. Pour finir, on dispose d'un graphe G = ({A₁, ..., A_n}, E), orienté et sans cycle, qui représente les contraintes de précédence entre les activités. (A_i, A_j) Î E signifie que dans toute solution, la date de fin de A_i est inférieure ou égale à la date de début de A_j. Toutes les données sont entières.

L'objectif est de trouver un ordonnancement, c'est-à-dire un ensemble de dates de démarrage pour chaque activité, qui respecte toutes les contraintes et dont la durée totale est minimum (la durée d'un ordonnancement étant définie par la différence entre la plus grande des dates de fin et la plus petite des dates de début).

Le RCPSP est un problème NP-difficile qui est très combinatoire. En 2003, il reste des instances à 40 activités pour lesquelles on ne connaît toujours pas la solution optimale !

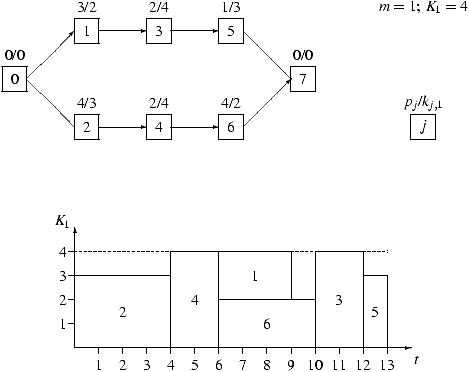
3 Un exemple

Dans l'exemple ci-dessous, 6 activités sont à exécuter sur une unique ressource de capacité 4. L'ordonnancement optimal est représenté sous la forme d'un ``diagramme de Gantt'' dans lequel chaque activité est modélisée par un rectangle (durée * nombre de machines utilisées).

4 Une méthode de résolution : les algorithmes de liste

Dans ce projet, on s'en tient à l'étude d'algorithmes approchés pour le RCPSP : on ne cherche donc pas le meilleur ordonnancement mais un ``bon'' ordonnancement réalisable.

Les méthodes sérielles [1], encore appelées ``algorithmes de liste'', sont basées sur une notion de priorité entre les activités. La priorité est calculée de façon heuristique et permet de choisir une activité à ordonnancer en premier parmi plusieurs candidates. Les méthodes sérielles permettent de construire très rapidement une solution du RCPSP.

Voici les éléments clefs des méthodes sérielles.

Les activités sont ordonnancées de gauche à droite en incrémentant le temps à partir de l'instant t = 0.
A l'instant t, les activités disponibles sont celles (1) non encore ordonnancées, (2) dont tous les prédécesseurs sont achevés et (3) qui disposent d'assez de machines sur chaque ressource pour s'exécuter.
S'il n'y a pas d'activité disponible, et si les activités ne sont pas déjà toutes ordonnancées, on incrémente t pour atteindre la prochaine date de fin parmi les activités déjà ordonnancées.
S'il y a des activités disponibles, on choisit parmi elles l'activité A_i de plus grande priorité. La date de début de A_i est alors fixée à t.

5 Les règles de priorité

La règle de priorité détermine complètement un ordonnancement de liste. Plusieurs règles de priorité peuvent être envisagées.

Priorité lexicographique : la priorité de A_i est i.
Plus grande durée : la priorité de A_i est p_i.
Plus grande durée étendue : la priorité de A_i est p_i + å_{(Ai, Aj) Î E} p_j .
Plus long chemin : la priorité de A_i est la longueur du plus long chemin issu de A_i
Chemin de plus grande durée : la durée d'un chemin est la somme des durées des activités sur le chemin, la priorité de A_i est alors la durée du chemin issu de A_i de plus grande durée.

En cas d'égalité (deux activités de même priorité), on favorisera systématiquement l'activité A_i de plus grand indice i.

Remarquons que l'ordonnancement de (3) correspond à la règle de priorité lexicographique.

6 Travail demandé

Vous devez faire un programme qui calcule les ordonnancements associés aux cinq règles de priorité mentionnées dans le paragraphe 5.

Vous utiliserez comme données les instances de la PSPLIB de Kolisch, Sprecher et Drexl : http://www.bwl.uni-kiel.de/Prod/psplib/library.html ¹. Vous testerez votre programme sur un sous ensemble directement téléchargeable des instances de la PSPLIB (http://www.hds.utc.fr/~baptiste/pub/ksd-for-X.zip). En annexe, le format d'une instance est sommairement commenté. Votre programme devra générer pour chaque instance cinq fichiers de solution qui indiquent une date de démarrage pour chaque activité. Vous analyserez les résultats obtenus en indiquant quelle règle semble être la meilleure.

Lors de la soutenance, votre programme sera testé sur un ou plusieurs autres fichiers de ce format par l'examinateur.

7 Extensions possibles

Les solutions construites par les algorithmes de liste peuvent être éloignées de l'optimum. Pour estimer la qualité de la solution, on cherche à calculer des bornes inférieures de la durée du projet.

La borne LB₀ est la longueur du plus grand chemin dans G. Sur l'exemple de (3), LB₀ = 10.
La borne LB_e est une borne ``énergétique''. Sur chaque ressource R_u, on calcule la durée minimale du projet en ignorant (1) les contraintes de précédence, (2) toutes les autres ressources R_v, v¹ u et (3) en supposant que les activités sont complètement déformables. Il s'agit alors de placer un travail total de å_i=1ⁿ p_i k_i,u unités sur une ressource de capacité K_u. La durée correspondante est alors éå_i=1ⁿ p_i k_i,u/K_u ù. On peut donc définir la borne énergétique :

LB_e =

max

1 £ u £ m
æ
ç
ç
è é
ê
ê
ê

n

å

i=1
p_i k_i,u

K_u
ù
ú
ú
ú ö
÷
÷
ø .
Sur l'exemple de (3), LB_e = é45/4 ù = 12.

Votre programme calculera la borne LB = max(LB₀, LB_e) et donnera pour chaque solution un majorant de l'écart relatif à l'optimum. Vous analyserez les résultats obtenus en indiquant laquelle des deux bornes semble être la meilleure.

Références

[1]: J. Carlier et Ph. Chrétienne. Problèmes d'ordonnancement. Masson (1988).

L'instance ``j3013_5.sm''

Le format des instances est indiqué précisément sur le site de la PSPLIB. L'instance ci-dessous est constituée de 32 activités (30 plus deux activités de durées nulles qui précèdent (succèdent) à toutes les autres) et de 4 ressources. Le tableau ``PRECEDENCE RELATIONS'' donne les successeurs de chaque advictivité (col jobnr.). Ainsi, le job 12 a 3 successeurs : 15, 20 et 21. La matrice ``REQUESTS/DURATIONS'' donne les durées des activités et pour chaque ressource le nombre de machines utilisées. Enfin, le tableau ``RESOURCEAVAILABILITIES'' donne les capacités des ressources. Les autres paramètres (horizon, nonrenewable, doubly constrained, pronr., rel.date, duedate, tardcost, MPM-Time, #modes) peuvent être ignorés.

************************************************************************ file with basedata : j30_29.bas initial value random generator: 205109436 ************************************************************************ projects : 1 jobs (incl. supersource/sink ): 32 horizon : 160 RESOURCES - renewable : 4 R - nonrenewable : 0 N - doubly constrained : 0 D ************************************************************************ PROJECT INFORMATION: pronr. #jobs rel.date duedate tardcost MPM-Time 1 30 0 43 14 43 ************************************************************************ PRECEDENCE RELATIONS: jobnr. #modes #successors successors 1 1 3 2 3 4 2 1 2 6 28 3 1 3 8 10 11 4 1 2 5 12 5 1 1 16 6 1 2 7 19 7 1 1 9 8 1 1 24 9 1 2 13 22 10 1 3 14 17 18 11 1 1 20 12 1 3 15 20 21 13 1 1 25 14 1 1 29 15 1 2 17 22 16 1 1 22 17 1 2 26 31 18 1 2 29 30 19 1 2 23 26 20 1 1 27 21 1 2 23 24 22 1 1 25 23 1 1 30 24 1 1 30 25 1 1 31 26 1 1 27 27 1 1 29 28 1 1 31 29 1 1 32 30 1 1 32 31 1 1 32 32 1 0 ************************************************************************ REQUESTS/DURATIONS: jobnr. mode duration R 1 R 2 R 3 R 4 ------------------------------------------------------------------------ 1 1 0 0 0 0 0 2 1 2 3 5 1 1 3 1 8 7 2 10 6 4 1 2 8 1 5 2 5 1 1 5 9 9 2 6 1 10 9 6 1 8 7 1 7 1 7 5 9 8 1 7 7 7 8 1 9 1 7 6 3 6 7 10 1 7 5 1 6 3 11 1 4 1 9 10 3 12 1 6 6 7 10 6 13 1 4 10 9 2 10 14 1 1 10 8 4 9 15 1 7 3 7 9 4 16 1 10 10 10 8 3 17 1 2 8 1 8 1 18 1 8 5 5 3 9 19 1 1 5 9 8 3 20 1 5 4 6 7 6 21 1 5 8 4 10 8 22 1 2 7 9 1 3 23 1 3 7 3 7 9 24 1 9 5 2 6 5 25 1 10 4 7 1 7 26 1 10 1 5 1 6 27 1 7 7 6 7 10 28 1 1 5 6 5 6 29 1 4 1 7 3 4 30 1 7 8 6 5 10 31 1 3 6 1 5 9 32 1 0 0 0 0 0 ************************************************************************ RESOURCEAVAILABILITIES: R 1 R 2 R 3 R 4 17 18 20 18 ************************************************************************

1: Attention, ce site n'est pas exclusivement dédié au ``pur'' RCPSP. Les auteurs considèrent aussi le cas où des activités peuvent s'exécuter selon différents ``modes''. Nous ne nous intéressons qu'au problème ``mono-mode'' et vous pouvez ignorer les rubriques ``multi-mode'' du site.

Ce document a été traduit de L^AT_EX par H^EV^EA.